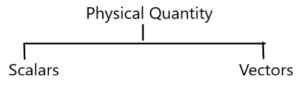
Scalars:-
Some physical quantities are completely described by only magnitudes (numerical value with the unit) and are added by a simple rule of algebra. Such physical quantities are called scalars. Ex- mass, time, distance, speed, etc.
Vectors:-
Some physical quantities are completely described by both magnitude and direction and are added according to the triangle rule of vector addition. such physical quantities are called vectors. Ex. Displacement, Velocity, Acceleration, force. etc
Representation of Vector:-
A vector can be represented by a straight line with an arrow-headed.
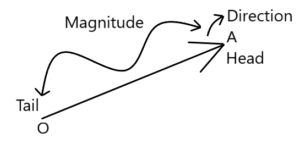
or
The magnitude of a vector is written as
or
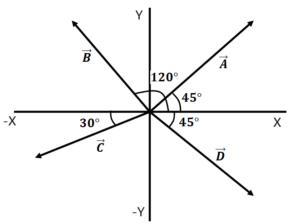
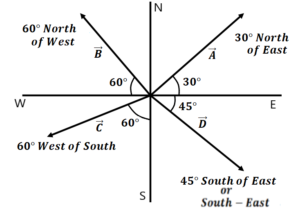
4 units and
from +x direction
6 units and
from +x axis
6 units and
from +x axis
7 units and
from +x axis or 7 units and
with +x axis
Types of Vectors:-
- Equal Vector:- Two vectors are said to be equal if they have the same magnitude and the same direction
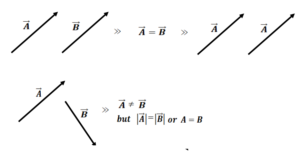
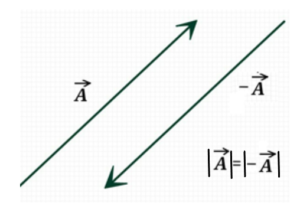
- Negative Vector:-Two vectors are said to be negative if they have the same magnitude but opposite direction
- Null/Zero Vector:- Vector having zero magnitudes and no specific direction is known as a Null vector.
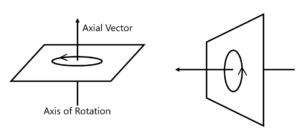
- Axial Vector:- The vectors which represent rotational effect and act along the axis of rotation in accordance with the right-hand screw(Thumb) rule are called axial vectors.
- Collinear Vector:- All vectors are collinear if they act along the same line. parallel vectors and antiparallel vectors are collinear vectors.

- Coplanar Vector:-All vectors are said to be coplanar if all lie in the same plane. Two vectors are always coplanar vectors.
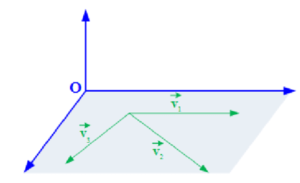
from fig are coplanar vectors
- Unit Vector:- A vector having a magnitude equal to one (unity) is known as a unit vector

A unit vector in the direction of a given vector is given by
i.e. any vector can be expressed as the magnitude times the unit vector along its own direction.i.e.
Conventionally unit vectors along the x,y, and z directions are denoted by
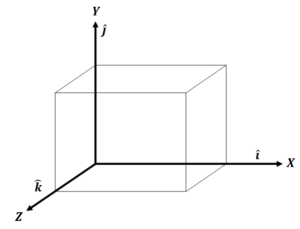
unit vector along x-axis,
unit vector along – x axis
unit vector along y-axis,
unit vector along -y axis
unit vector along the z-axis,
unit vector along -z axis
Ex- Here vector A has a magnitude of 3 units along the x-axis.
| Question 1. Represent the following
a. c. e. A vector having magnitude 3 units along |
NOTE:-
- Scalars have +ve or -ve values but magnitudes of vectors are always +ve.
- If a vector is multiplied by a +ve number then only its magnitude will be changed but if multiplied by a -ve number then its both magnitude and direction will be changed.
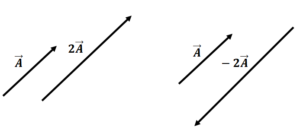
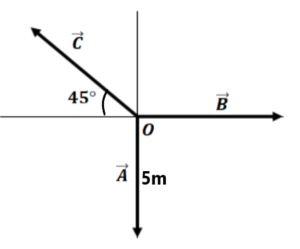
| Question 2:- A vector of magnitude 5 units makes an angle of |
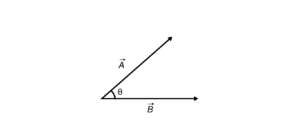
Angle Between Two Vectors:-
The angle between two vectors is the acute angle formed when their tails coincide.
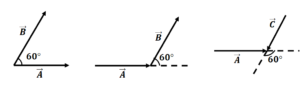
| Question 3:- Find the angle between
|
| Question 4:- Find the angle between vectors
|
Addition of Vectors:-
Triangle Law (For Two Vectors):-
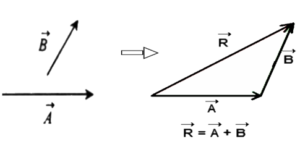
We can write
The magnitude of the resultant is given by where
is the angle between
The direction of the resultant=( see parallelogram law)
Parallelogram Law ( For Two Vectors):-
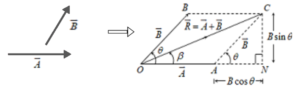
We can write
The magnitude of the resultant is given by where
is the angle between
The direction of the resultant vector with is
NOTE:-
a. if θ=0°

(Maximum magnitude)
The direction of R is the same as
b. if θ=180°
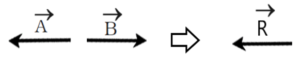 if A>B
if A>B
(Minimum Magnitude)
The direction of R is the same as along a larger vector
c. if θ=90°
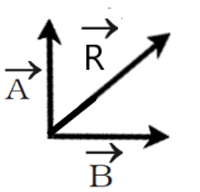
Its direction is , Here
is the angle of resultant with vector
| Click For Practice Questions |
Subtraction of Two Vectors:-
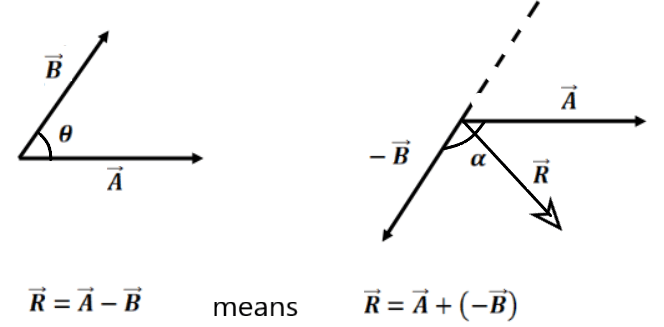
if θ is the angle between , then the magnitude of
if given by
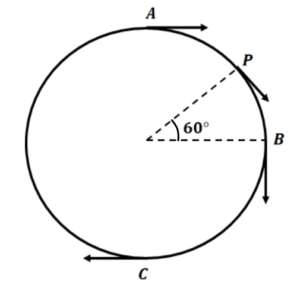
| Question 27:- Vector (a) Question 28:- If two vectors Question 29:- The resultant of two unit vectors is a unit vector. Find the magnitude of the difference between the two unit vectors. Question 30:- two vectors of equal magnitude 5 units have an angle 60° between them. Find the magnitude of (a) The sum of the vectors (b) the difference between the vectors Question 31:- A car is moving on a circular track with constant speed v=20 m/s. Find the change in velocity (a) From A to C (b) From A to B (c) From A to P Question 32:- Vector |
Polygon Rule of Vector Addition:-
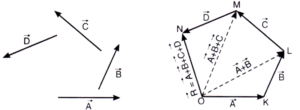
| Question 33:-
Draw the resultant of the following (a) |
Resolution of Vector:-
The splitting of a vector into two or more components is known as the resolution of the vector.
In two rectangular components:-
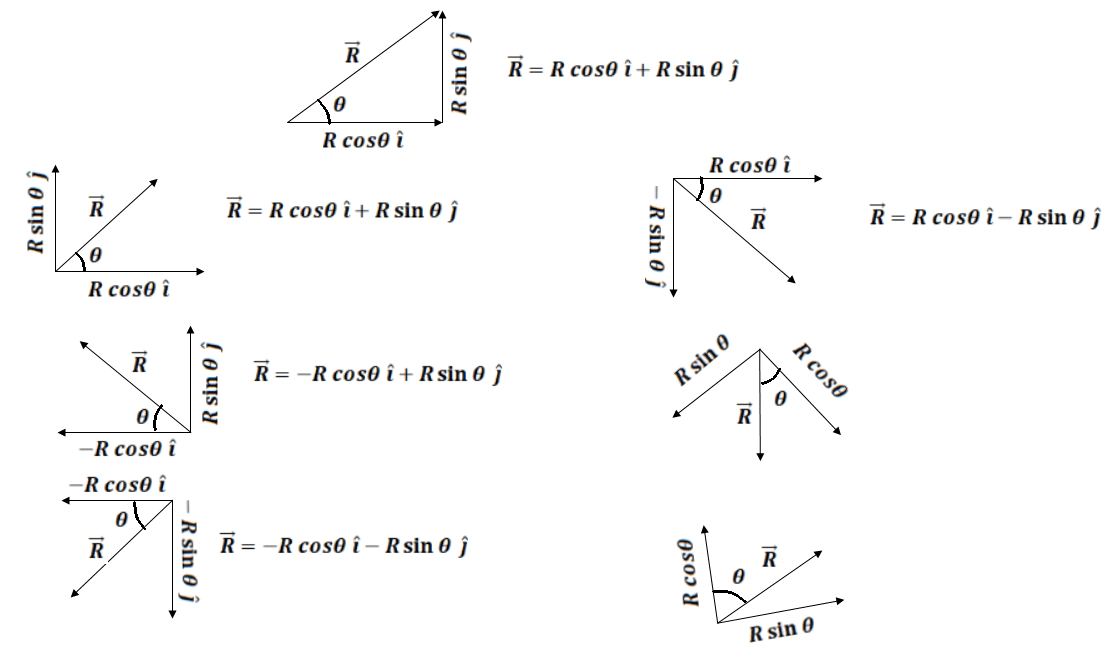
Here Its magnitude
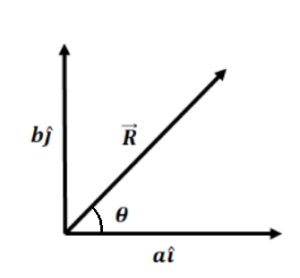
and it’s direction
In three rectangular components:-

here
its magnitude
If R, makes an angle α, β and γ with X, Y and Z axis respectively.
Then we can write
i.e
Here are called direction cosine
Now,
| Q.1. Find the magnitude and direction of the following vectors with the +ve X- axis.
(a) (e) Q.2. A particle is moving with velocity v=100 m/s. If one of the rectangular components of a velocity is 50 m/s. Find the other component of velocity. Q.3. A man rows a boat with a speed of 18 km/h in the N-W direction. The shoreline makes an angle of 15° south of west. Obtain the components of the velocity of the boat along the shoreline and perpendicular to the shoreline. Q.4. if Q.5. A boat is moving in a direction Q.6. A car is moving with a speed of 10 m/s. Write the velocity vector of car in unit vector notation. If it is moving (a) in the direction of N-E (b) N-W (c) S-W and (d) S-E Q.7. Write the following vector in component form.
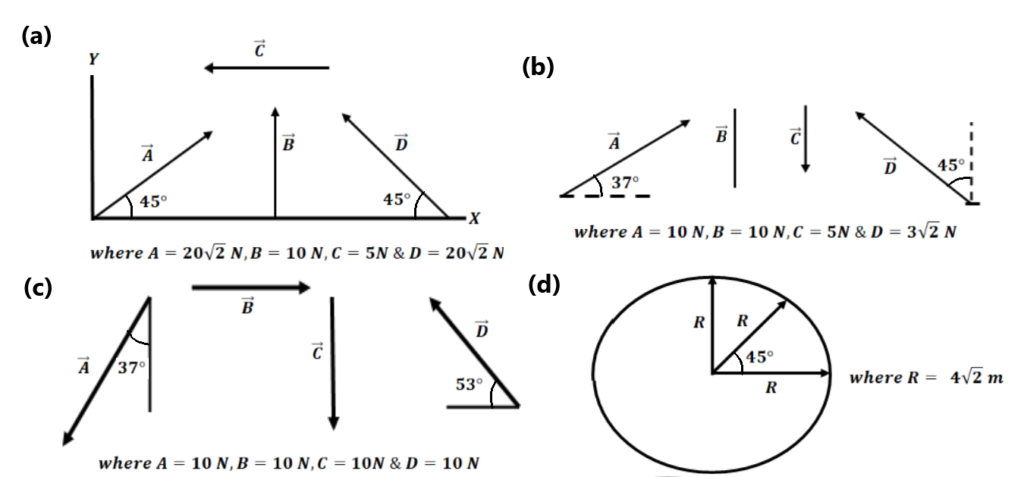
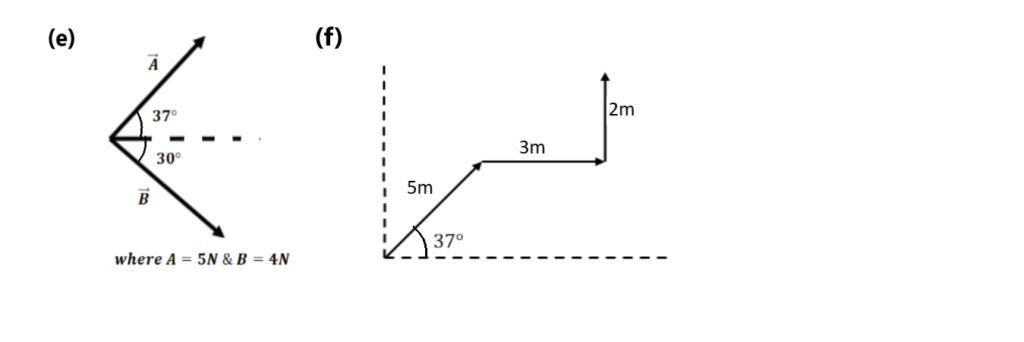
Q.8. Find the resultant of the following vectors.
Q.9. A vector of magnitude 20√2 is in a direction making an angle of 60° with the x-axis and 60° with the z-axis, write the vector in component form. Q.10. A vector having magnitude 20 units makes an angle of 60° with the x-axis and 60° with the y-axis. Find the vector. Q.11. x-component of vector Q.12.Find a vector of magnitude 5 units which is parallel to vector Q.13. Find a vector whose magnitude is equal to that of Q.14. If Q.15. Q.16. Given Q.17. Find the
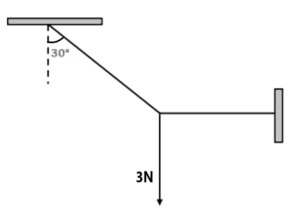
Q.18. Given Q.19. Find the tension force in the string.
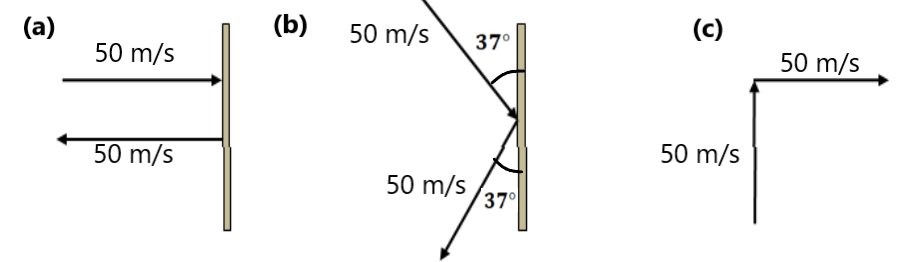
Q.20. Vector Q.21. Find the change in velocity ( magnitude and direction) as shown in fig.
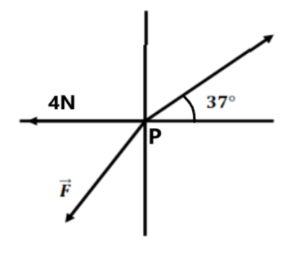
Q.22. Determine the vector which when added to the resultant of Q.23. If Q.24. If and find (a) Q.25. Let Q.26. A vector Q.27. If Q.28. The sum of three vectors as shown in fig is zero. Find the magnitude of
Q.29. Find the unit vector parallel to the resultant of vectors |
Multiplication of Two Vectors:-
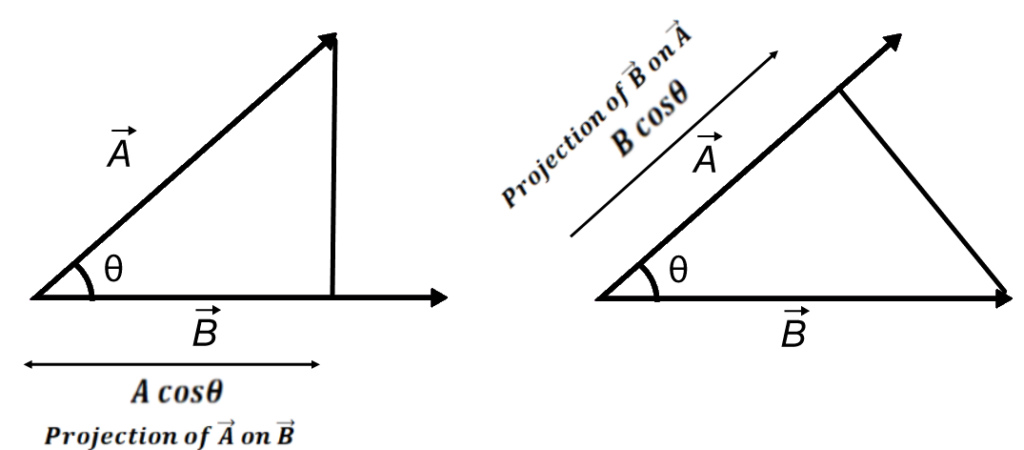
1. Dot Product (Scalar Product):-
where θ is the angle between and
.
NOTE:-
1.
i.e
2.
if θ=0° then
If θ=180° then
If θ=90° then
3.
4.
5.
6.
7.
then
| Q.1. If Q.2. Prove that Q.3. if Q.4. Proove that Q.5. if Q.6. if Q.7. The vectors Q.8. Find the component of the vector Q.9. Find the magnitude of the projection of vector Q.10. Find the component of Q.11. Find the angle between the x-axis and the vector Q.12. If Q.13. Find the value of m so that the vectors Q.14. Find the angle between Q.15. If the sum of the two unit vectors is a unit vector, then find the magnitude of their difference. Q.16. Prove that Q.17. If Q.18. if Q.19. if Q.20. A body, acted upon by a force of 50N, is displaced through a distance 10m in a direction making an angle of 60° with a force. Find the work done by the force. Q.21. A particle moves from position |
2. Cross Product (Vector Product):-
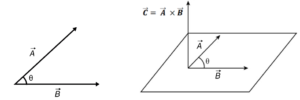
where θ is the angle between and
is the unit vector perpendicular to both
. The direction of the cross product is from the screw rule or right-hand thumb rule.
NOTE:-
1. If
If
2.
3.
4.
5.
5.
then,
6. The magnitude of the cross product of two vectors is equal to the area of the parallelogram formed by them.

Prove:-
Area of triangle =
area of parallelogramme=
| Q.1. Find the cross product of (a) (b) (c) (d) Q.2. Determine the area of the parallelogram whose adjacent sides are Q.3. Show that vector Q.4. Find a unit vector perpendicular to both the vectors Q.5. If Q.6. Show that Q.7. If Q.8. Prove that Q.9. Calculate the area of the triangle determined by the two vectors. Q.10. Prove that Q.11. Determine the unit vector parallel to the cross-product of the vectors Q.12. If Q.13. |

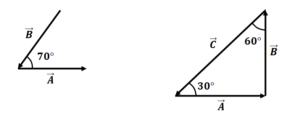
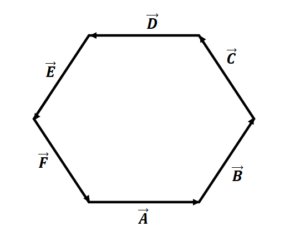 Note that the interior angle of a regular hexagon is
Note that the interior angle of a regular hexagon is