प्रकाश के कला संबध स्रोत ( Coherent Source of Light )
दो प्रकाश के स्रोत कला सम्बद्ध कहलाते है यदि वे समान आवृत्ति , समान तरंगदैर्घ्य तथा समान कला में या समान कलांतर में तरंग उत्सर्जित करे ।
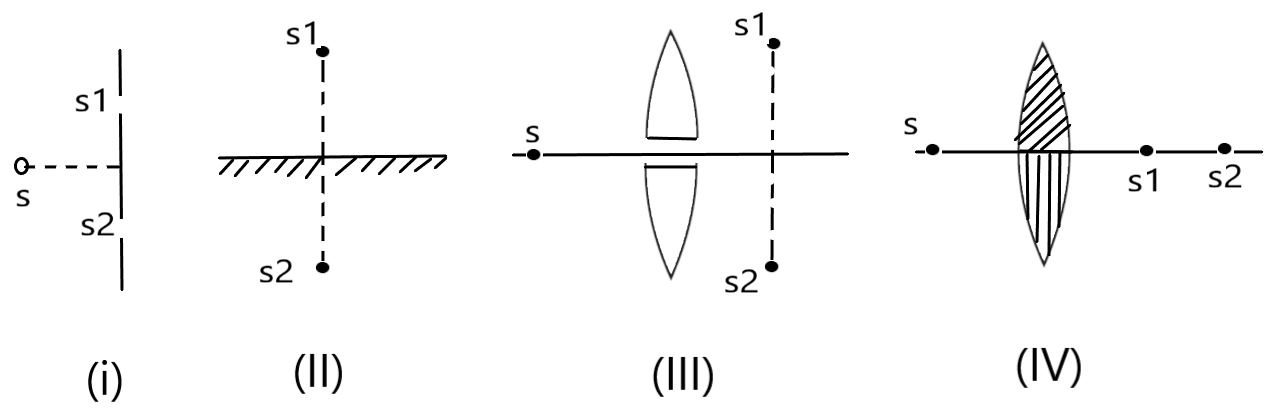
चित्र में स्रोत तथा
दो कला सम्बद्ध स्रोत है । दो कला सम्बद्ध स्रोत ही व्यतिकरण प्रभाव को प्रदर्शित करते है । दो कला असम्बद्ध स्रोत कभी भी व्यतिकरण प्रभाव को प्रदर्शित नहीं करती है ।
अध्यारोपण का सिद्धांत ( Superposition Principle )
अध्यारोपण के सिद्धांत के अनुसार किसी भी क्षण पर एक कण का परिणामी विस्थापन दो या दो से अधिक तरंगों के कणो के अलग – अलग विस्थापनों का सदिश योग के बराबर होता है ।
अर्थात
जहाँ किसी क्षण पहले , दूसरे , तीसरे ,….. तरंगों के कणों का विस्थापन है । जहाँ
उसी क्षण परिणामी तरंग का विस्थापन है ।
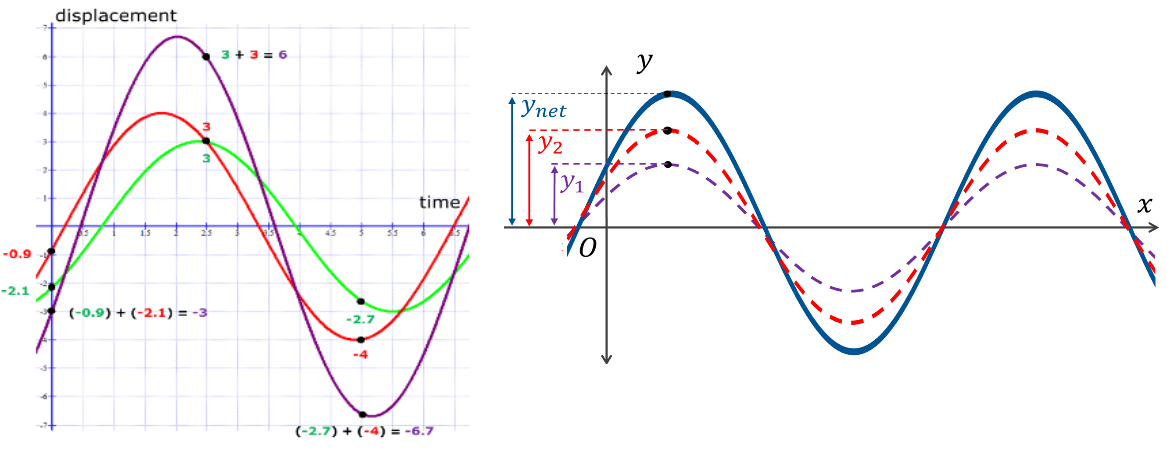
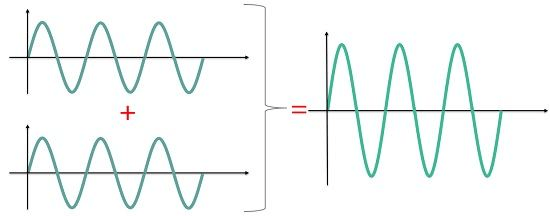
(1) सम्पोषी अध्यारोपण (Constructive Interference)
जब दो कला सम्बन्ध तरंगे एक दूसरे पर समान कला में अध्यारोपित होती है अर्थात एक तरंग का श्रृंग दूसरी तरंग के श्रृंग पर तथा एक का गर्त दूसरे के गर्त पर हो , तब इस अध्यारोपण को सम्पोषी अध्यारोपण कहते है । यदि दोनों तरंगों का आयाम समान हो तो सम्पोषि अध्यारोपण में परिणामी आयाम दुगुना हो जाता है ।
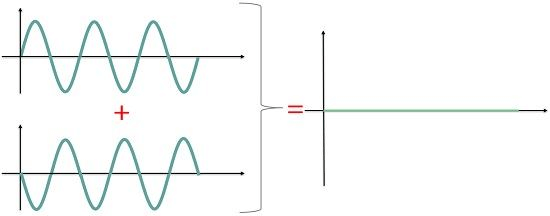
(2) विनाशी अध्यारोपण (Destructive Interference)
जब दो कला सम्बन्ध तरंगे एक दूसरे पर विपरीत कला में अध्यारोपित होती है अर्थात एक तरंग का श्रृंग दूसरी तरंग के गर्त पर तथा एक का गर्त दूसरे के शीर्ष पर हो , तब इस अध्यारोपण को विनाशी अध्यारोपण कहते है । यदि दोनों तरंगों का आयाम समान हो तो विनाशी अध्यारोपण में परिणामी आयाम शून्य हो जाता है ।
प्रकाश का व्यतिकरण (Interference of light)
हम जानते है की प्रकाश की ऊर्जा प्रकाश तरंग के आयाम के वर्ग के समानुपाती होती है अर्थात प्रकाश का एकल स्रोत से उत्सर्जित ऊर्जा सभी दिशाओं में समान रूप से फैलता है क्योंकि सभी जगह आयाम समान रहती है ।
परन्तु जब प्रकाश के दो कला सम्बद्ध स्रोत से उत्सर्जित तरंगें अध्यारोपित होती है तब प्रकाश ऊर्जा का वितरण असमरूप होता है । माध्यम के कुछ बिंदुओं पर प्रकाश की तीव्रता , संपोषी अध्यारोपण के कारण अधिकतम तथा इसके विपरीत माध्यम के कुछ बिंदुओं पर विनाशी अध्यारोपण के कारण प्रकाश की तीव्रता न्यूनतम होती है । तरंगों की इस घटना को ही प्रकाश का व्यतिकरण कहते है ।
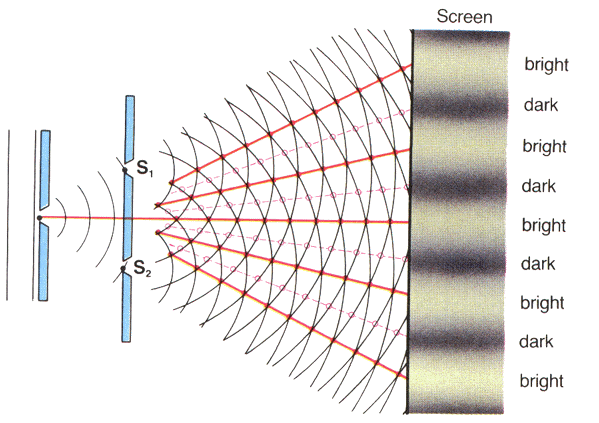
प्रकाश का व्यतिकरण तथा ऊर्जा संरक्षण का सिद्धांत
व्यतिकरण की घटना में व्यतिकरण तरंगों की कुल ऊर्जा नियत रहती है । इसमें ऊर्जा का केवल पुनर्वितरण होता है । न्यूनतम तीव्रता ( विनाशी अध्यारोपण ) के स्थान पर जितनी ऊर्जा विलुप्त होती है उतनी ही अतिरिक्त ऊर्जा अधिकतम तीव्रता ( संपोषी अध्यारोपण ) के स्थान पर प्रकट हो जाती है । अतः व्यतिकरण की घटना ऊर्जा संरक्षण के नियम के अनुकूल है ।
कलांतर तथा पथांतर में सम्बन्ध
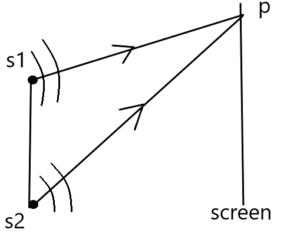
चित्र के अनुसार,
P बिंदु पर तरंगों का पथांतर =
माना की तथा
से निकला तरंग P बिंदु पर अध्यारोपित होती है। यदि तरंगों के मध्य पथांतर
हो तो उनके बीच कलांतर
होगी ।
अर्थात पथांतर के लिए कलांतर होगी
∴ 1 पथांतर के लिए कलांतर होगी
∴ पथांतर के लिए कलांतर होगी
व्यतिकरण का सिद्धांत (Theory of Interference )

माना की तथा
दो एकवर्णी कला सम्बद्ध स्रोत है , जहाँ से
तरंगदैर्घ्य की प्रकाश तरंगे उत्सर्जित हो रही है । माना की प्रत्येक तरंग का आयाम A तथा कोणीय आवृति ω है तथा दोनों तरंगे P बिंदु पर अध्यारोपित होती है जहाँ दोनों का विस्थापन क्रमशः
तथा
है। अर्थात
जहाँ , P बिंदु पर दोनों तरंगों के बीच का कलांतर है
अध्यारोपण के सिद्धांत के अनुसार , P बिंदु पर परिणामी तरंग का विस्थापन होगा
यहाँ पर P बिंदु पर परिणामी तरंग का आयाम है ।
अतः P बिंदु पर परिणामी तीव्रता होगी ।
हम जानते है की
( एकल स्रोत की तीव्रता )
इस व्यंजक से साफ़ साफ़ पता चलता है की P बिंदु पर प्रकाश का परिणामी तीव्रता दोनों तरंगो के कालांतर पर निर्भर करता है जब दोनों तरंगे P बिंदु पर अध्यारोपित होती है ।
संपोषी व्यतिकरण के लिए , जब परिणामी तीव्रता महत्तम होगी
हम जानते है की ,
अर्थात संपोषी व्यतिकरण के लिए
कलांतर = (
)
पथांतर = (
)
अर्थात जब दो कलासम्बद्ध तरंगे एक बिंदु पर अध्यारोपित होती है और यदि उसके बीच कलांतर तथा पथांतर
हो तो उसे संपोषी व्यतिकरण कहते है और उस स्थिति में उस बिंदु पर प्रकाश की तीव्रता अधिकतम ( एकल स्रोत का 4 गुना ) हो जाती है ।
विनाशी व्यतिकरण के लिए , जब परिणामी तीव्रता न्यूनतम होगी
उसी प्रकार पथांतर होगा
अर्थात विनाशी व्यतिकरण के लिए
कलांतर =
पथांतर =
अर्थात जब दो कलासम्बद्ध तरंगे एक बिंदु पर अध्यारोपित होती है और यदि उसके बीच कलांतर तथा पथांतर
हो तो उसे विनाशी व्यतिकरण कहते है और उस स्थिति में उस बिंदु पर प्रकाश की तीव्रता न्यूनतम ( शून्य ) हो जाती है ।
NOTE:-
(1) सभी दीप्त फ़्रीज़ों की तीव्रता समान रहती है तथा सभी अदीप्त फ्रिंज़ों की तीव्रता समान रहती है
(2) यदि दो कला सम्बद्ध स्रोत का व्यतिकरण होता है तो किसी भी बिंदु पर कलांतर समय के साथ नहीं बदलेगा । अतः हमें स्थिर व्यतिकरण पैटर्न प्राप्त होगा । अर्थात समय के साथ महत्तम तथा न्यूनतम की स्थितियां नहीं बदलती है ।
परन्तु यदि कलांतर समय के साथ बहुत तेजी के साथ बदलता है तो महत्तम तथा न्यूनतम की स्थितियां भी तेजी से बदलेगी तथा हमें औसत तीव्रता वितरण प्राप्त होगा ।
वास्तव में ऐसा तब होता है जब दो अलग अलग प्रकाश स्रोत किसी पर्दा को प्रकाशित करता है ।

(3) जब दो तरंगों का आयाम अलग अलग हो जैसे तथा
(
), तब परिणामी तरंग का परिणामी आयाम R होगा
हम जानते है की ![]()
अर्थात उपर्युक्त समीकरण से हम लिख सकते है ,
संपोषी व्यतिकरण के लिए
तथा
विनाशी व्यतिकरण के लिए
तथा
उसी प्रकार हम जानते है की , प्रकाश की तीव्रता स्रोत की चौड़ाई के समानुपाती होती है । माना की तथा
क्रमशः स्रोत
तथा
की चौड़ाई है ।
उचित तीव्रता का व्यतिकरण बनाये रखने की शर्तें
- दो स्रोत, प्रकाश के कला सम्बद्ध स्रोत होने चाहिए ।
- दो प्रकाश के स्रोतों को लगातार प्रकाश तरंगें उत्पन्न करनी चाहिए ।
- प्रकाश के दो कला सम्बद्ध स्रोतों के द्वारा उत्सर्जित तरंगों के आयाम दीप्त और अदीप्त फ्रिंज में पूर्ण स्पष्टता प्राप्त करने के लिए बराबर होने चाहिए ।
- प्रकाश के दोनों कला सम्बद्ध स्रोत बहुत संकरे होने चाहिए ।
- प्रकाश के कला सम्बद्ध स्रोतों से परदे की दुरी कम नहीं होनी चाहिए ।
- प्रकाश एकवर्णीय होनी चाहिए ।
- दोनों प्रकाश स्रोतों के बीच की दुरी बहुत कम होनी चाहिए , अन्यथा फ्रिंज चौड़ाई इतनी कम हो जाएगी की वे दिखाई नहीं पड़ेंगे ।
व्यतिकरण प्रभाव के दैनिक जीवन से उदाहरण
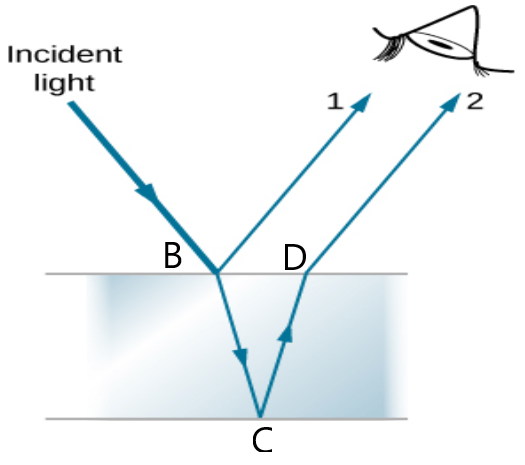
हमे गीली सड़क पर वाहनों से रिसे तेल के कारण सड़क पर वर्ण रेखाएं दिखाई देती है । यह वर्ण रेखाएं पानी पर तेल की फिल्म की ऊपर तथा निचे की परतों से परावर्तित प्रकाश के व्यतिकरण के कारण दिखाई देती है । इसी प्रकार साबुन के बुलबुले धुप में रंगीन दिखाई पड़ते है क्योंकि प्रकाश की किरणें बुलबुले से परावर्तित होती है, जिनका व्यतिकरण होता है । इसी प्रकार मोर तथा अन्य पंक्षी व्यतिकरण के कारण बहुरंगी दिखाई पड़ते है ।
अभ्यास के लिए आंकिक प्रश्न(1) यदि यंग के प्रयोग में दो स्लिट की चौड़ाई 16:1 के अनुपात में है , व्यतिकरण प्रतिरूप में अधिकतम और न्यूनतम तीव्रता के अनुपात की गणना कीजिये । (25:9) (2) एक ही आवृत्ति तथा एक ही आयाम a की दो प्रकाश तरंगें किसी बिंदु पर एक साथ पहुँच रही है । तरंगों के बीच कितना कलांतर हो की परिणामी तरंग का आयाम (a) 2a (b) a√2 (c) a तथा (d) 0 हो ( 0°, 90°, 120°, 180°) (3) यंग के प्रयोग में व्यतिकरण प्रतिरूप में उच्चिष्ठ और निम्निष्ठ पर प्रकाश तीव्रता का अनुपात 4:1 है ।दोनों स्लिट की चौड़ाई का अनुपात ज्ञात करें ।(9:1) (4) समान आवृत्ति और समान आयाम ‘a’ की दो तरंगें एक साथ एक बिंदु तक पहुँच रही है । दो तरंगों में मध्य कलांतर क्या होगा ताकि परिणामी तरंग का आयाम है (a) √3a तथा (b) a (60°, 120°) (5) दो तरंगों की तीव्रताओं का अनुपात 16:9 है । उनके आयामों का अनुपात क्या है ? यदि दोनों तरंगें व्यतिकरण करें , तो महत्तम तथा न्यूनतम तीव्रताओं का अनुपात ज्ञात कीजिये । (49:1) (6) किसी माध्यम में एक बिंदु पर समान आयाम a तथा समान आवृत्ति n की दो प्रकाश तरंगें 270° कलांतर में गुजरती है । इस बोण्डु पर परिणामी तरंग का आयाम क्या होगा ? ( a√2) (7) समान आवृत्ति की दो तरंगें जिनके आयामों का अनुपात 3:5 है, एक दूसरे पर अध्यारोपित होती है । परिणामी तरंग की महत्तम तथा न्यूनतम तीव्रताओं का अनुपात बताइये । (16:1) (8) 1mm और 2 mm आयाम की दो तरंगें एक समान दिशा में एक माध्यम में संचारित होती है । परिणामी आयाम ज्ञात करें उन बिंदुओं पर जहाँ कलांतर है (a) π/3 (b) π (√7 mm , 1 mm) (9) I तथा 4I तीव्रताओं के दो स्रोतों तरंगों के बीच व्यतिकरण की घटना हो रही है । उन बिंदुओं पर तीव्रताओं की गणना कीजिये जहाँ कलांतर (a) π/2 (b) π (5I,I) (10) यंग के व्यतिकरण प्रयोग में स्लिट्स की चौड़ाई का अनुपात 1:9 है, व्यतिकरण प्रतिरूप में अधिकतम और न्यूनतम पर तीव्रताओं का अनुपात ज्ञात कीजिये ।(4:1) (11) यंग के व्यतिकरण प्रतिरूप में स्लिट्स चौड़ाई में अनुपात 9:4 है । व्यतिकरण प्रतिरूप में उच्चिष्ठ और निमनिष्ठ पर तीव्रताओं के अनुपात की गणना करे ।( 25:1) (12) व्यतिकरण प्रतिरूप में दीप्त और अदीप्त पर प्रकाश की तीव्रताओं का अनुपात 9:1 है । दोनों स्लिट्स की चौड़ाई का अनुपात ज्ञात करें । ( 4:1) (13) यंग के द्वी स्लिट्स प्रयोग में पर्दे पर दो बिंदुओं की तीव्रता का अनुपात ज्ञात कीजिये , जब दो स्लिट्स से तरंगें निम्न पथांतर रखती हो (a) 0 (b) λ/4 (2:1) (14) प्रकाश के दो कला सम्बद्ध स्रोत a और 2a आयाम की तरंगें उत्सर्जित करते है । वे दोनों स्रोतों से समान दुरी पर स्थित बिंदु P पर मिलते है । यदि प्रथम तरंग की तीव्रता I हो, तो बिंदु पर परिणामी तीव्रता क्या होगी ? ( 9I) |
प्रकाश तरंगों का व्यतिकरण तथा यंग का प्रयोग ( यंग का द्वी – क्षिरी प्रयोग )
प्रकाश का व्यतिकरण की घटना 1801 – 1802 ईस्वी में थॉमस यंग के द्वारा प्रेक्षित की गई । जिस प्रयोग सेटअप द्वारा यंग ने व्यतिकरण की घटना को प्रयोग करके दिखाया था , वह निम्न प्रकार है ।
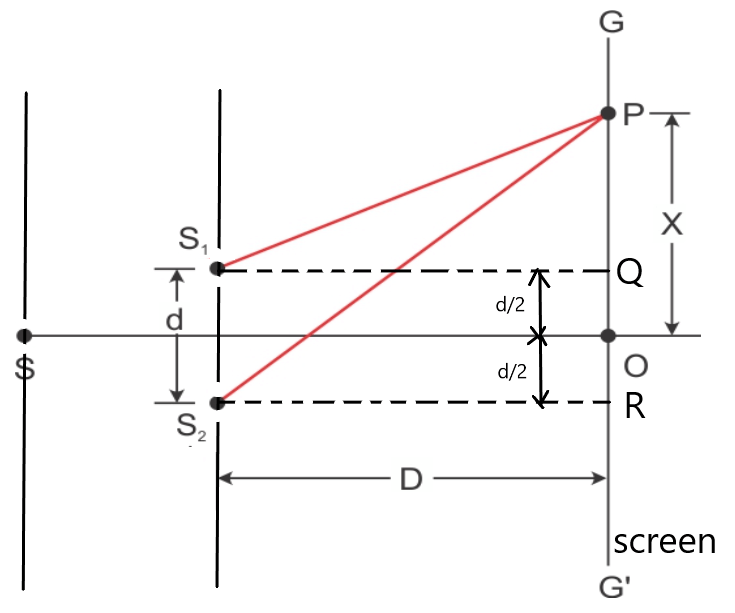
चित्र के अनुसार एक एकवर्णी प्रकाश को बारीक स्लिट S पर गिरने दिया । स्लिट S से प्रकाश तरंगों को दो बारीक स्लिट तथा
पर जाने दिया जो एक दूसरे से बहुत निकट और समान्तर थी ।
तथा
,
से समान दुरी पर थी अतः ये दोनों स्रोत कलासम्बद्ध स्रोत की तरह व्यवहार करती है । इस तरंगों को एक दूसरे पर अध्यारोपित किया गया जिसके कारण दीप्त तथा अदीप्त फ्रिंजे समान्तर रखे परदे में प्राप्त किये गए । परदे को
तथा
से एक निश्चित दुरी पर रखा जाता है ।
माना दोनों स्लिट तथा
के मध्य की दुरी d है । इन बिंदुओं से परदे की लंबवत दुरी D है तथा छिद्रों से निकलने वाले प्रकाश की तरंगदैर्घ्य
है । माना की
तथा
से निकलने वाला प्रकाश तरंग , परदे में P बिंदु पर मिलता है । यहाँ पर ये समान कला या विपरीत कला में भी हो सकते है यह इस बात पर निर्भर करेगा की
तथा
से P बिंदु का पथांतर कितना है । माना की O से P की दुरी x है।
यहाँ पर पथांतर =
उसी प्रकार
∴ पथांतर =
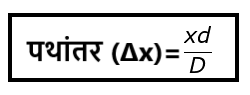
संपोषी / रचनात्मक व्यतिकरण के लिए ( दीप्त फ्रिंज की स्थिति )
यहाँ पर पथांतर =
यह दीप्त फ़्रिंजों का O से दुरी है ।
( केंद्रीय दीप्त फ्रिंज)
( प्रथम दीप्त फ्रिंज की दुरी O से )
( द्वितीय दीप्त फ्रिंज की दुरी O से)
……………………………..
……………………………..
( n वे दीप्त फ्रिंज की दुरी O से)
रचनात्मक व्यतिकरण के लिए ( दीप्त फ्रिंज की स्थिति )
यहाँ पर पथांतर =
यह अदीप्त फ़्रिंजों का O से दुरी है ।
( प्रथम अदीप्त फ्रिंज की दुरी O से)
( द्वितीय अदीप्त फ्रिंज की दुरी O से)
( तृतीय अदीप्त फ्रिंज की दुरी O से)
……………………………..
……………………………..
( n वे अदीप्त फ्रिंज की दुरी O से)
फ्रिंज की चौड़ाई ( Fring width)
दो क्रमागत दीप्त तथा क्रमागत अदीप्त फ़्रिंजों के मध्य दुरी को फ्रिंज चौड़ाई कहते है । इसे प्रायः द्वारा सूचित किया जाता है ।
अर्थात
दीप्त फ़्रिंजों के लिए
NOTE:-
चूँकि लाल रंग का तरंगदैर्घ्य बैगनी रंग से अधिक होता है इसीलिए लाल रंग के लिए फ्रिंज की चौड़ाई बैगनी रंग के फ्रिंज की चौड़ाई से अधिक होती है ।
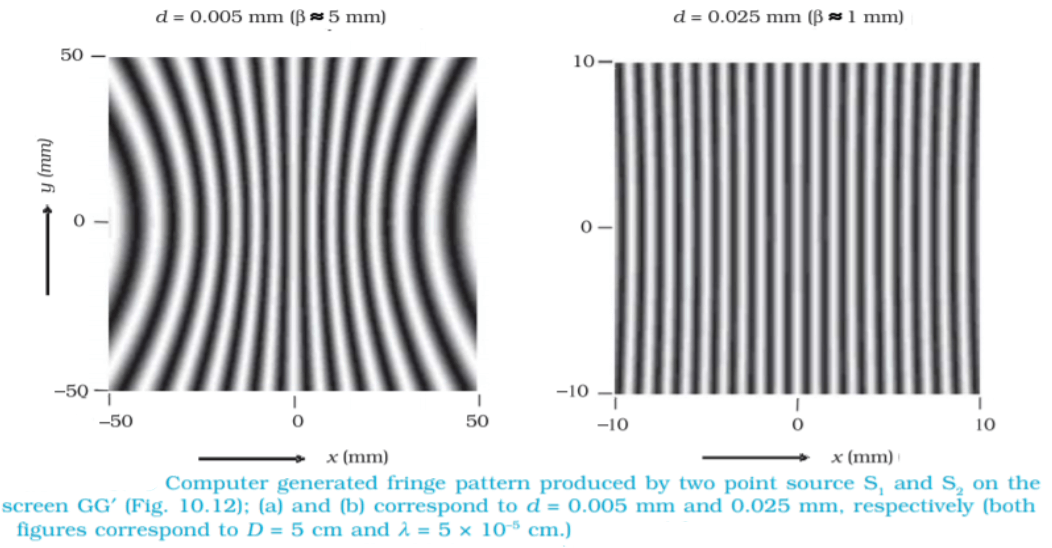
यदि स्रोत
तथा
बिंदु स्रोत हो या रेखीय स्रोत ( क्षीरियाँ) हो , दोनों स्थिति में हमें सीधी रेखा फ्रिंज प्राप्त होगा । लेकिन क्षीरियाँ के स्थिति में फ्रिंज की तीव्रता अधिक होगी ।
फ्रिंज की कोणीय चौड़ाई को निम्न रूप से लिख सकते है
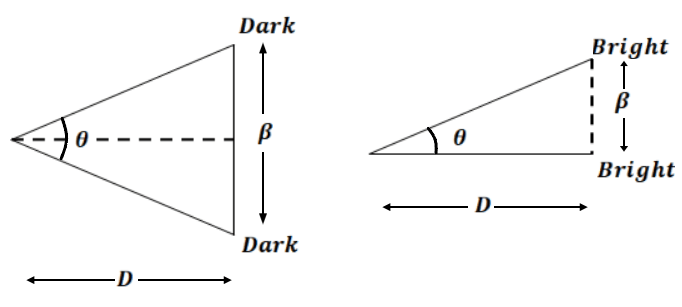
छोटे कोण के लिए
फ्रिंज की कोणीय चौड़ाई ( कोणीय पार्थक्य ) अचर रहती है और यह परदे की स्थिति पर निर्भर नहीं करती है ।
हम जानते है की
अचर राशि है
परदे में स्थित बिंदु P का बिन्दुपथ (Locus) इस प्रकार होगा की पथांतर () अचर होगी । अर्थात केवल केंद्रीय फ्रिंज एक सरल रेखा में होगी बाकी सभी फ्रिंज अति परवलयकार होगा । यदि दुरी D फ्रिंज चौड़ाई की अपेक्षा बहुत अधिक होगी , तो फ्रिंजे काफी हद तक सीधी रेखाओं में होंगी ।
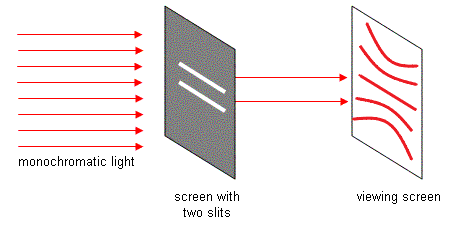
यंग के द्वी – क्षिरी प्रयोग में , यदि स्रोत S को थोड़ा सा स्लिट के समान्तर कुछ कोण से दूर ले जाते है तो केंद्रीय दीप्त फ्रिंज भी उतना हो कोण से दूसरी तरफ परदे पर प्राप्त होती है , क्योंकि O बिंदु पर स्रोत से निकला तरंग का पथांतर शून्य होती है ।
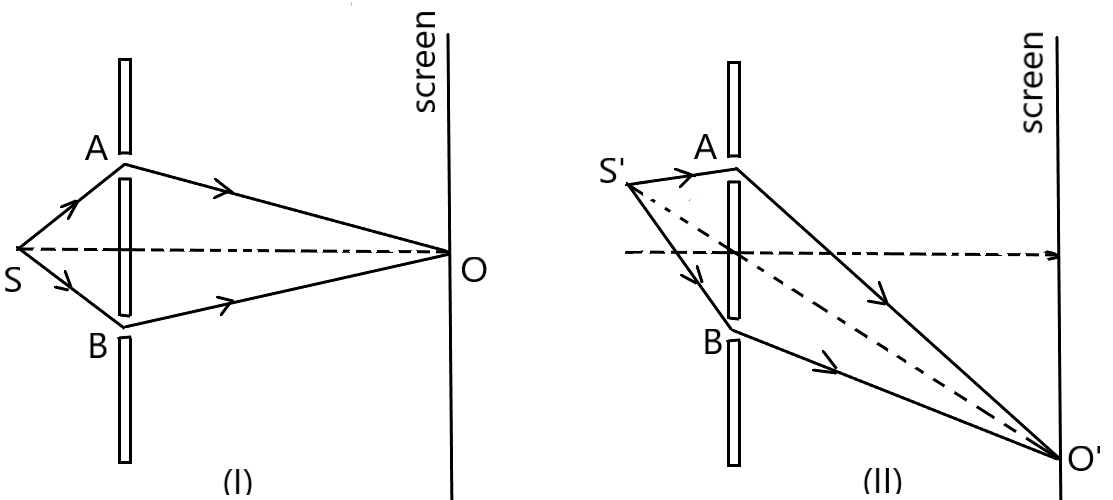
यदि एक स्लिट को बंद कर दिया जाये तो हमें किसी भी प्रकार का फ्रिंज प्राप्त नहीं होगा। इससे यह पता चलता है की व्यतिकरण पैटर्न सिर्फ दो कला सम्बद्ध स्रोत के अध्यारोपण से ही प्राप्त किये जा सकते है ।
व्यतिकरण फ़्रिंजों को देखने के लिए यह सरत पूरी होनी चाहिए ।
जहाँ तथा
के बीच की दुरी है ,
स्लिट
की चौड़ाई है
जब उपर्युक्त उपकरण को किसी तरल पदार्थ में डुबोया जाता है जिसका अपवर्तनांक
है , तब
अर्थात प्रकाश का तरंगदैर्घ्य घटेगा , इसीलिए फ्रिंज की चौड़ाई
कम हो जाएगी ।
यदि एकवर्णी प्रकाश की जगह श्वेत प्रकाश को प्रयोग में लाया जाये तो केंद्र में सफ़ेद फ्रिंज बनता है जिसके दोनों तरफ कुछ रंगीन फ्रिंज बनता है ।
अभ्यास के लिए आंकिक प्रश्न(1) यंग के प्रयोग में रेखा छिद्रों के बीच की दुरी 0.2 सेमी है और उन्हें 5896 Å तरंगदैर्घ्य के प्रकाश से प्रकाशित किया गया है । यदि रेखा छिद्रों से परदे की दुरी 1 मीटर हो , तो परदे पर बनने वाली व्यतिकरण फ़्रिंजों की चौड़ाई ज्ञात कीजिये ? ( 0.3 mm) (2) यदि यंग के प्रयोग में दो रेखा छिद्रों के बीच की दुरी 0.03 cm , रेखा – छिद्रों के तल से परदे की दुरी 1.5 मीटर तथा केंद्रीय फ्रिंज से चतुर्थ दीप्त फ्रिंज की दुरी 1.0 सेमी हो, तो प्रयुक्त प्रकाश की तरंगदैर्घ्य ज्ञात कीजिये । (5000Å) (3) एक दूसरे से (4) यंग के प्रयोग में दो स्लिटों के बीच की दुरी 0.3 mm है । स्लिटों से 0.6 मीटर दूर स्थित परदे पर केंद्रीय फ्रिंज से 10 वी दीप्त फ्रिंज 1.2 सेमी दूर है । प्रयुक्त प्रकाश की तरंगदैर्घ्य ज्ञात कीजिये । (6000Å) (5) यंग के प्रयोग में प्रकाश की तरंगदैर्घ्य 6000 Å है । स्लिटों के बीच की दुरी 0.05 सेमी तथा स्लिटों से पर्दे की दुरी 1 मीटर है । प्रथम अदीप्त एवं प्रथम दीप्त फ्रिंज के बीच की दुरी ज्ञात कीजिये । (0.6 mm) (6) यंग के प्रयोग में पर्दे की द्विक रेखा छिद्रों से दुरी 1.0 मीटर है । जब 5000Å तरंगदैर्घ्य का प्रकाश रेखा छिद्रों पर डाला जाता है तो पर्दे पर प्राप्त फ़्रिंजों की चौड़ाई 1.0 मिमी है । रेखा छिद्रों के बीच अंतराल ज्ञात कीजिये । ( 0.5 मिमी ) (7) यंग के द्वी स्लिट प्रयोग में दूर रखे पर्दे पर फ़्रिंजों की कोणीय चौड़ाई 1° प्राप्त होती है । यदि 6000 Å तरंगदैर्घ्य का प्रकाश प्रयुक्त हुआ हो , तो स्लिटों के बीच की दुरी कितनी है ? (0.0344 mm) (8) यंग के प्रयोग में 4000Å तरंगदैर्घ्य का प्रकाश प्रयुक्त करने पर फ्रिंज की चौड़ाई 0.60 सेमी प्राप्त होता है । यदि पर्दे की स्लिटों से दुरी आधी कर दी जाये , तो किस तरंगदैर्घ्य के प्रकश के लिए फ्रिंज की चौड़ाई 0.40 सेमी प्राप्त होगा ? ( 5333 Å) (9) यंग के द्वी स्लिट के प्रयोग में दोनों स्लिटों के बीच की दुरी 3.0 मिमी है तथा वे 480 nm तरंगदैर्घ्य के प्रकाश से प्रकाशित है । यदि पर्दे की स्लिटों से दुरी 2.0 मीटर हो, तो पर्दे पर केंद्रीय दीप्त फ्रिंज से आठवीं दीप्त फ्रिंज तथा तीसरी दीप्त फ्रिंज के बीच दुरी ज्ञात कीजिये । ( 1.760 मिमी ) (10) यंग के प्रयोग में स्लिटों के बीच की दुरी 0.5 mm है । प्रयुक्त प्रकाश की तरंगदैर्घ्य 6000Å है तथा स्लिटों से पर्दे की दुरी 2.0 मीटर है । केंद्रीय फ्रिंज से (a) चतुर्थ अदीप्त फ्रिंज तथा (b) चतुर्थ दीप्त फ्रिंज की दुरी ज्ञात कीजिये (c) फ्रिंज की चौड़ाई भी ज्ञात कीजिये । (11) यंग के प्रयोग में 6000Å तरंगदैर्घ्य का प्रकाश प्रयुक्त करने पर फ्रिंज की चौड़ाई 2 मिमी प्राप्त होता है । यदि पूरा उपकरण 1.33 अपवर्तनांक वाले द्रव में डुबो दिया जाये , तो अब फ्रिंज की चौड़ाई क्या होगी ? (1.5 मिमी ) (12) यंग के द्वी स्लिट प्रयोग में कुछ दुरी पर रखे पर्दे पर व्यतिकरण फ्रिंजे प्राप्त होती है । पर्दे को स्लिटों की ओर (13) यंग के प्रयोग में लाल प्रकाश (λ=7200Å) प्रयुक्त करने पर दृष्टि क्षेत्र में 60 फ्रिंजे दिखाई देती है । नीला प्रकाश (λ=4800Å) प्रयुक्त करने पर कितनी फ्रिंजे दिखाई देगी ? ( 90) (14) यंग के प्रयोग में , 6000Å तरंगदैर्घ्य के प्रकाश द्वारा 2 mm की फ्रिंज चौड़ाई प्राप्त होती है । फ्रिंज चौड़ाई की गणना कीजिये यदि सम्पूर्ण उपकरण 1.33 अपवर्तनांक के तरल माध्यम में डुबो दिया जाये । (1.5 mm) |
लघु उत्तरीय प्रश्न(1) कला सम्बद्ध स्रोतों से क्या तात्पर्य है ? (a) प्रकाश की तरंगदैर्घ्य बढ़ाई जाये (1) प्रकाश में व्यतिकरण के लिए यंग के द्वी – रेखा छिद्र प्रयोग का सिद्धांत समझाइये तथा व्यतिकरण फ्रिन्जो की चौड़ाई के लिए व्यंजक प्राप्त कीजिये । (2) प्रकाश के व्यतिकरण की आवश्यक शर्तें क्या है ? |
