प्रकाश का परावर्तन -

प्रस्तावना :-

प्रकाश हमारे जीवन का एक महत्वपूर्ण हिस्सा है । यह ऊर्जा का एक महत्वपूर्ण रूप है जिस पर हम प्रतिदिन निर्भर रहते है । इसके बिना हम अपने आसपास की दुनिया को नहीं देख सकते है । लेकिन प्रकाश हम तक कैसे पहुंचता है? और यह हमारी दुनिया को देखने के तरीके को कैसे प्रभावित करता है? यहाँ पर हम प्रकाश पर विस्तारपूर्वक चर्चा करने जा रहे है । भौतिकी की वह शाखा जिसमे प्रकाश की प्रकृति और उसके गुणों का अध्ययन किया जाता है , प्रकाशिकी कहलाती है ।

प्रकाश :-

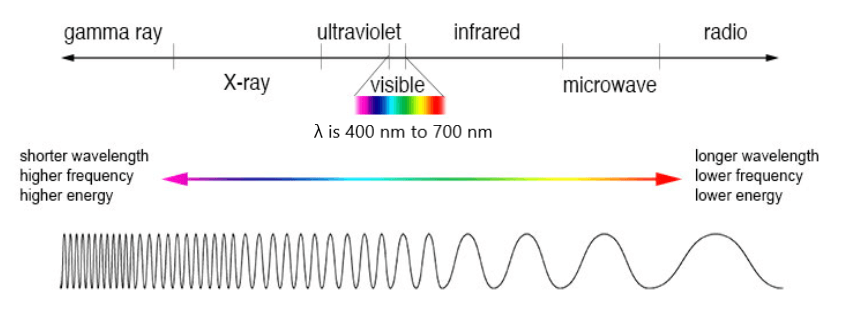
प्रकाश वह कारक है जिसकी मदद से हम वस्तुओं को देख पातें है लेकिन प्रकाश स्वयं अदृश्य होता है । प्रकाश विधुत चुम्बकीय तरंग है । मानव आंख (रेटिना) विधुत चुम्बकीय तरंगों की स्पेक्ट्रम की एक छोटी सी सीमा (400 nm से 700 nm ) के भीतर उत्तेजित होकर वस्तुओं को देखने में मदद करती है ।

क्या हम प्रकाश को देख सकते है ?

नहीं , हम केवल प्रकाश के मार्ग में आने वाली वस्तुओं को ही देख सकते है ।

दृष्टि के लिए और क्या चाहिए ?

प्रकाश, आँख तथा वस्तु

लेकिन क्या सभी परिमित आकार की वस्तुएँ दिखाई देंगी यदि प्रकाश और उसे देखने के लिए आँख हो?

नहीं , पूर्ण पारदर्शी सतह तथा पूर्ण परावर्तक दर्पण को हम नहीं देख सकते है क्योंकि यह दोनों , अपने ऊपर आपतित किरण को किसी भी प्रकार से परिवर्तित नहीं करती है , और वह सभी 100% किरण को परावर्तित कर देती है जिसके कारण हमारी आँखे उस वस्तु को महसूस नहीं कर पाती है, जिससे हम उस वस्तु को नहीं देख पाते है ।

यहाँ पर प्रकाश का परिवर्तन का अर्थ है किसी वस्तु द्वारा आंशिक रूप से प्रकाश को अवशोषित करना और/या प्रकाश को बिखेरना (Scattering of light)

सामान्य अनुभव से हम प्रकाश के बारे में दो बातें जानते है की , प्रकाश सीधी रेखा में गमन करती है , तथा निर्वात में प्रकाश की चाल सबसे अधिक ( $light$ ) होती है

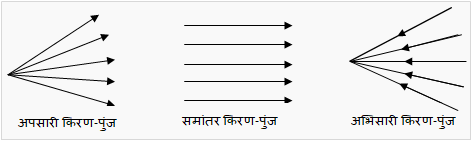
प्रकाश के अत्यंत संकीर्ण पथ की दिशा को प्रकाश की किरण (Beam of Light) कहते हैं। प्रकाश की किरण को तीर वाली सीधी रेखा द्वारा प्रदर्शित किया जाता है। जब बहुत सी किरणें एक साथ हो जाती है तो किरणों के समूह को किरण पुंज कहते हैं।

प्रकाश कण या तरंग :-

इस प्रश्न का की “प्रकाश कण है या तरंग” , बहुत रोचक और लम्बा इतिहास है ।

न्यूटन के अनुसार , प्रकाश कणों का एक संग्रह है जिसे कणिकाएं कहा जाता है जो स्रोत द्वारा उत्सर्जित होते है और ये कणिकाएं सीधी रेखा में गमन करती है । इसे प्रकाश का कनिका का सिद्धांत कहते है । इस सिद्धांत के आधार पर न्यूटन ने प्रकाश के परावर्तन और अपवर्तन के नियमों की व्याख्या की । लेकिन प्रकाश की कनिका प्रकृति के आधार कई प्रकाशीय परिघटनाओं की व्याख्या नहीं की जा सकी ।

डच भौतिक वैज्ञानिक क्रिस्टियन हाइगेन्स जो न्यूटन के समकालीन थे ने सुझाव दिया की प्रकाश एक तरंग घटना हो सकती है और छोटी तरंगदैर्घ्य के कारण प्रकाश सीधी रेखा में गमन करती है । लेकिन थॉमस यंग के व्यतिकरण प्रयोग और फ्रेनेल का विवर्तन प्रयोग के कारण यह निश्चित रूप से स्थापित हो गया की प्रकाश एक तरंग घटना है ।

लेकिन ड्रामा अभी भी खत्म नहीं हुआ था । चरमोत्कर्ष तब आया जब प्रकाश का तरंग सिद्धांत प्रकाश विधुत प्रभाव को व्याख्या करने में विफल रहा ।

Q> लेकिन प्रश्न अभी भी यही था की प्रकाश कण है या तरंग ?

Ans> प्रकाश कण के साथ साथ तरंग प्रकृति का है जिसे द्वैत प्रकृति कहते है और प्रकाशीय घटनाओं के आधार पर प्रकाश की प्रकृति ( कण या तरंग की ) होती है । बाद में यह पाया गया की इलेक्ट्रान जैसे कण भी द्वैत प्रकृति के होते है ।

प्रकाश का परावर्तन :-

प्रकश की किरणे जब एक माध्यम से चलकर किसी दूसरे माध्यम की तल से टकराती है और टकराकर पहले माध्यम में निश्चित दिशा में लौट आती है , तो यह घटना प्रकाश का परावर्तन कहलाती है ।

प्रकाश के परावर्तन का नियम :- प्रकाश के परावर्तन के दो नियम है

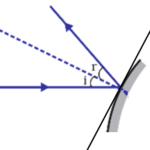
आपतित किरण , परावर्तित किरण तथा आपतन बिंदु पर खिंचा गया अभिलम्ब तीनो एक ही समतल में होते है ।
आपतन कोण तथा परावर्तन कोण आपस में बराबर होते है । $\fn_cm (\angle i=\angle r)$

NOTE:-

यदि आपतित किरण दर्पण के लंबवत आपतित होती है तो परावर्तन के बाद किरण उसी पथ पर विपरीत दिशा में वापस लौट आती है ।

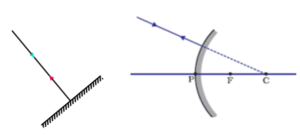
परावर्तन का नियम सभी प्रकार के सतहों ( अवतल , उत्तल ) के लिए मान्य है ।

वस्तु तथा प्रतिबिम्ब :-

किसी वस्तु की अवधारणा प्रकाश के परावर्तन और अपवर्तन की घटना से पहले की है और एक प्रतिबिम्ब की अवधारणा प्रकाश के परावर्तन और अपवर्तन की घटना के बाद की है ।

वस्तु :- वस्तु उसे कहते है जिससे प्रकाश की किरणे निर्गत होती है , वस्तु दो प्रकार के होते है दीप्त तथा अदीप्त वस्तु ।

प्रतिबिम्ब :- वस्तु के किसी बिंदु से आती हुई प्रकाश की किरणे परावर्तन अथवा अपवर्तन के बाद जिस बिंदु पर मिलती है या आती हुई प्रतीत होती है उसे उस बिंदु का प्रतिबिम्ब कहते है

प्रतिबिम्ब , वास्तविक ( जब किरणे वास्तव में मिलती है ) तथा आभासी ( जब किरणे अपसृत होती हुई प्रतीत हो ) दोनों प्रकार के होते है

NOTE:-

1> वस्तु भी वास्तविक तथा आभासी होते है ।

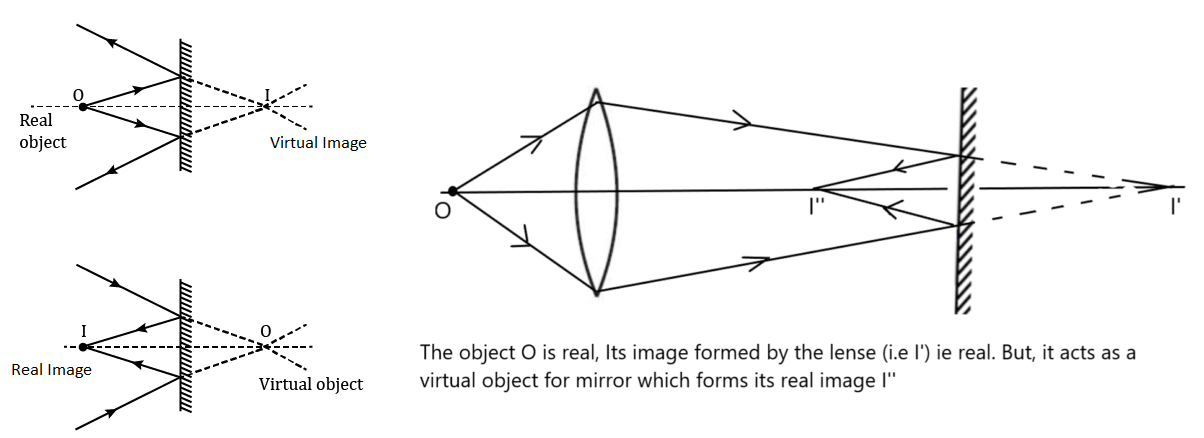
2> सड़क , दीवार , चट्टान आदि खुरदरी सतहों पर जब प्रकाश आपतित होता है , तब वह विभिन्न दिशाओं में परावर्तित हो जाता है । इसे विसरित अथवा अनियमित परावर्तन कहते है । विसरित परावर्तन से प्रतिबिम्ब नहीं बनता है ।

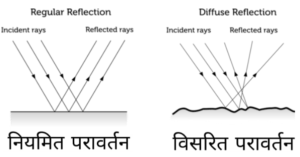
Q> हम आभासी प्रतिबिम्ब को कैसे देख पाते है ?

Ans> आभासी प्रतिबिम्ब को परदे पर प्राप्त नहीं किया जा सकता है , लेकिन उन्हें हमारी आँखों से देखा जा सकता है । क्योंकि हमारी आँख के लेंस के लिए , यह आभासी प्रतिबिम्ब एक वस्तु की रूप में कार्य करती है और अंत में हमारी आँख का लेंस हमारे रेटिना पर इसका वास्तविक प्रतिबिम्ब बनाती है । इसीलिए हम एक आभासी प्रतिबिम्ब को देख सकते है

समतल दर्पण से प्रकाश के परावर्तन सम्बन्धी कुछ निष्कर्ष :-

1> समतल दर्पण से वस्तु की दुरी तथा प्रतिबिम्ब की दुरी परस्पर बराबर होती है ।

2> प्रतिबिम्ब का आकार वस्तु के आकार के बराबर होता है ।

3> वस्तु तथा उसके प्रतिबिम्ब में पार्श्व परिवर्तन हो जाता है ।

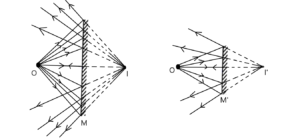
4> बड़े द्वारक वाले दर्पण द्वारा बना प्रतिबिम्ब छोटे द्वारक वाले दर्पण द्वारा बना प्रतिबिम्ब से ज्यादा साफ़ होती है क्योंकि बड़े दर्पण द्वारा बने प्रतिबिम्ब ज्यादा प्रकाश पुंज से मिलकर बने होते है ।

5> अपना पूरा प्रतिबिम्ब समतल दर्पण में देखने के लिए दर्पण की न्यूनतम लम्बाई मनुष्य की लम्बाई की आधी होती है ।

6> दृष्टि क्षेत्र :-

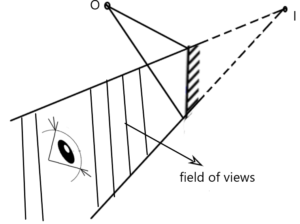
7> आपतित किरण की दिशा नियत रखते हुए यदि समतल दर्पण को θ कोण से घुमा दिया जाए , तो परावर्तित किरण दर्पण के घूमने की दिशा में 2θ कोण से घूम जाती है ।

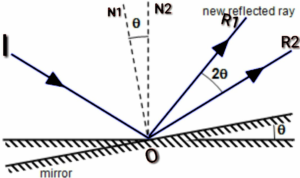
8> यदि दो समतल दर्पण एक दूसरे से θ कोण पर झुके हो तो उनके बीच रखे वस्तु की प्रतिबिम्ब की संख्या θ कोण पर निर्भर करता है ।

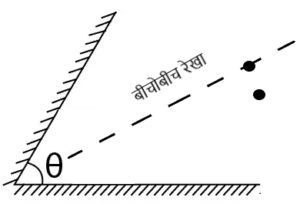
यदि $\fn_cm \frac{360^0}{\theta}$ एक सम संख्या हो , तो प्रतिबिम्ब की संख्या होगी $\fn_cm \left [ N=\frac{360^0}{\theta}-1 \right ]$ वस्तु के किसी भी स्थिति के लिए
यदि $\fn_cm \frac{360^0}{\theta}$ एक विषम संख्या हो, तो प्रतिबिम्ब की संख्या होगी $\fn_cm \left [ N=\frac{360^0}{\theta} \right ]$ यदि वस्तु दर्पण के बीचोबीच रेखा में न हो , $\fn_cm \left [ N=\frac{360^0}{\theta}-1 \right ]$ यदि वस्तु दर्पण के बीचोबीच रेखा में हो।
यदि $\fn_cm \frac{360^0}{\theta}$ एक पूर्णांक संख्या न हो , तो प्रतिबिम्ब की संख्या $\fn_cm \left [ N=\frac{360^0}{\theta} \right ]$ का पूर्णांक होगी ।

9> यदि वस्तु दर्पण के सामने v वेग से गतिमान है तो प्रतिबिम्ब की गति विपरीत दिशा में v होगी , लेकिन वस्तु के सापेक्ष प्रतिबिम्ब की गति 2v विपरीत दिशा में होगी ।

गोलीय दर्पण :-

गोलीय दर्पण खोखले गोले का एक भाग होता है जिसकी एक सतह पर पॉलिश ( चांदी की कलई ) कर दी जाती है ।

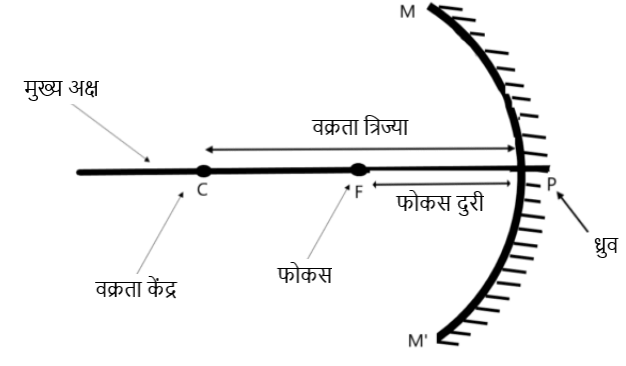
द्वारक :- गोलीय दर्पण के परावर्तक तल की बाहरी वृताकार रेखा के व्यास को दर्पण का द्वारक कहते है । चित्र में $\fn_cm M{M}'$ दर्पण का द्वारक है ।

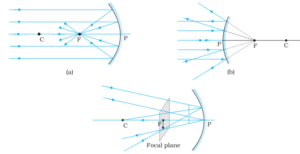
फोकस :- मुख्य अक्ष के समान्तर आने वाली किरणे दर्पण से परावर्तन के बाद मुख्य अक्ष पर जिस बिंदु पर मिलती है ( अवतल दर्पण में ) या मिलती हुई प्रतीत होती है ( उत्तल दर्पण में ) , वह बिंदु दर्पण का फोकस कहलाता है । फोकस से होकर गुजरने वाले तथा मुख्य अक्ष के लम्बवत समतल को फोकस तल कहते है । आपस में समान्तर सभी किरणे गोलीय दर्पण से परावर्तन के बाद फोकस तल के किसी बिंदु पर मिलती है अथवा मिलती हुई प्रतीत होती है ।

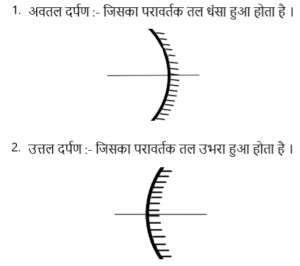
गोलीय दर्पण दो प्रकार के होते है ।

महत्वपूर्ण किरण आलेख :-

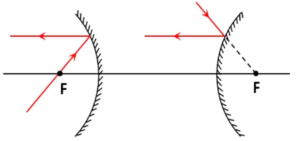
मुख्य अक्ष के समान्तर आती हुई किरणे परावर्तन के बाद फोकस से गुजरती है या फोकस से आती हुई प्रतीत होती है ।
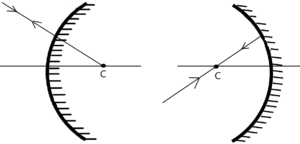
जो किरण गोलीय दर्पण के वक्रता केंद्र से होकर गुजरती है वह परावर्तन के बाद उसी मार्ग से वापस लौट जाती है ।
जो किरण ध्रुव पर मुख्य अक्ष के साथ जितनी कोण से आपतित होती है , परावर्तन के बाद उतनी ही कोण से पार्श्व दिशा में चली जाती है ।

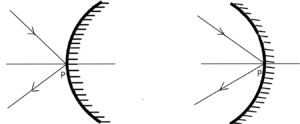
नवीन कार्तीय चिन्ह परिपाटी :-

u→ वस्तु दुरी

v→ प्रतिबिम्ब दुरी

f→ फोकस दुरी

R→ वक्रता त्रिज्या

सभी दूरिया गोलीय दर्पण के ध्रुव से मापी जाती है ।
आपतित प्रकाश की दिशा में मापी गयी दूरियाँ +ve मानी जाती है जबकि वे दूरियाँ जिनको आपतित प्रकाश की विपरीत दिशा में मापा जाता है , -ve मानी जाती है ।
मुख्य अक्ष के लम्बवत ऊपर की ओर मापी जाने वाली दूरियाँ +ve मापी जाती है जबकि निचे की ओर मापी गयी दूरियाँ -ve मापी जाती है ।

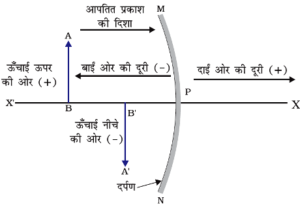
उपाक्षीय किरण :- जो किरण मुख्य अक्ष के बहुत ही निकट से गुजरती है , उसे उपाक्षीय किरण कहते है । छोटे द्वारक के लिए किरण उपाक्षीय किरण होती है ।

फोकस दुरी तथा वक्रता त्रिज्या के बीच में सम्बन्ध :-

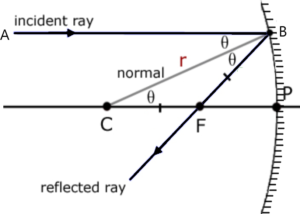
माना की छोटे द्वारक का एक अवतल दर्पण है , जिसका ध्रुव , फोकस तथा वक्रता केंद्र क्रमशः P, F & R है । माना की मुख्य अक्ष के समान्तर एक किरण परावर्तन के बाद फोकस से होकर गुजरती है ।

चित्र के अनुसार

$\fn_cm \angle ABC=\angle CBF$ ( परावर्तन के नियम के अनुसार )

$\fn_cm \angle ABC= \angle BCF$ ( एकान्तर कोण )

$\fn_cm \therefore \;\angle CBF=\angle BCF$ अर्थात $\fn_cm \Delta BCF$ एक समद्विबाहु त्रिभुज होंगे ।

$\fn_cm \therefore BF=FC$

छोटे द्वारक के लिए B तथा P एक ही बिंदु पर केंद्रित होंगे

अर्थात $\fn_cm PF=FC$

अतः हम कह सकते है की बिंदु F अर्थात फोकस P और C के बीच होंगे ।

$\fn_cm \therefore PF= \frac{PC}{2}\;\;\;\;\;\;\;\;\;\left [ f=\frac{R}{2} \right ]$

◊ दर्पण सूत्र

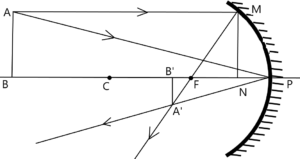
माना की AB एक वस्तु है जो अवतल दर्पण के सामने मुख्य अक्ष पर लंबवत स्थित है । बिंदु P , F तथा C दर्पण का क्रमशः ध्रुव, फोकस तथा वक्रता केंद्र है ।
परावर्तन के बाद वस्तु का एक आभासी, उल्टा तथा छोटा प्रतिबिम्ब $\fn_cm {A}'{B}'$ बनता है जैसा की चित्र में दिखाया गया है ।
चित्र के अनुसार

$\Delta APB$ aur $\Delta A'PB'$ समरूप त्रिभुज होंगे

i.e $\fn_cm \frac{AB}{A'B'}= \frac {PB}{PB'}$ ————————–(1)

उसी प्रकार $\Delta MFN$ and $\Delta A'FB'$ समरूप त्रिभुज होंगे

i.e $\fn_cm \frac{MN}{A'B'}= \frac{NF}{FB'}$

$\fn_cm \frac{AB}{A'B'}=\frac{NF}{FB'}$

छोटे द्वारक के लिए P और N एक ही बिंदु पर केंद्रित होंगे ।

अतः हम लिख सकते है

$\fn_cm \frac{AB}{A'B'}=\frac{PF}{FB'}$ ——————————(2)

समीकरण (1) और (2) से

$\fn_cm \Rightarrow \frac{PB}{PB'}=\frac{PF}{FB'}$

$\fn_cm \Rightarrow \frac{PB}{PB'}=\frac{PF}{PB'-PF}$

चिन्ह परिपाटी के अनुसार ,

PB=-u, PB’= -v, PF= -f

अर्थात ,

$\fn_cm \large \Rightarrow \frac{-u}{-v}=\frac{-f}{-v+f}$

$\fn_cm \large \Rightarrow uv - uf =vf$

दोनों तरफ $\fn_cm uvf$ से भाग देने पर

$\fn_cm \large \Rightarrow \frac{uv}{uvf}-\frac{uf}{uvf}=\frac{vf}{uvf}$

$\fn_cm \large \Rightarrow \frac{1}{f}-\frac{1}{v}=\frac{1}{u}$

$\fn_cm \LARGE \left [ \frac{1}{v}+\frac{1}{u}=\frac{1}{f} \right ]$

proof mirror formula

NOTE:- बिद्यार्थी खुद से उत्तल दर्पण द्वारा दर्पण सूत्र का व्यंजक स्थापित करें ।

◊ रेखीय आवर्धन

रेखीय आवर्धन हमें यह बतलाता है की दर्पण द्वारा बना प्रतिबिम्ब वस्तु से कितना गुना बड़ा या छोटा है । अर्थात प्रतिबिम्ब की ऊंचाई तथा वस्तु की ऊंचाई के अनुपात को ही रेखीय आवर्धन कहते है । इसे m द्वारा सूचित किया जाता है

अर्थात $\fn_cm \left [ m=\frac{h_2}{h_1} \right ]$

जहाँ $\fn_cm h_2\rightarrow$ प्रतिबिम्ब की ऊंचाई तथा $\fn_cm h_1\rightarrow$ वस्तु की ऊंचाई है ।

NOTE:- यदि प्रतिबिम्ब और वस्तु एक दूसरे से उल्टा हो तो $\fn_cm m$ का मान -ve होगा ।

ऊपर के चित्र के अनुसार ( दर्पण सूत्र से )

$\fn_cm \frac{A'B'}{AB}=\frac{PB'}{PB}$

$\fn_cm \frac{-h_{2}}{h_{1}}=\frac{-v}{-u}$

$\fn_cm \frac{h_{2}}{h_{1}}=\frac{-v}{u}$

$\fn_cm \LARGE \left [ m=-\frac{v}{u} \right ]$

NOTE:- आभासी प्रतिबिम्ब के लिए $\fn_cm m$ +ve तथा वास्तविक प्रतिबिम्ब के लिए $\fn_cm m$ -ve होता है

◊ गोलीय दर्पण से प्रतिबिम्बों का बनना

अवतल द◊र्पण के लिए

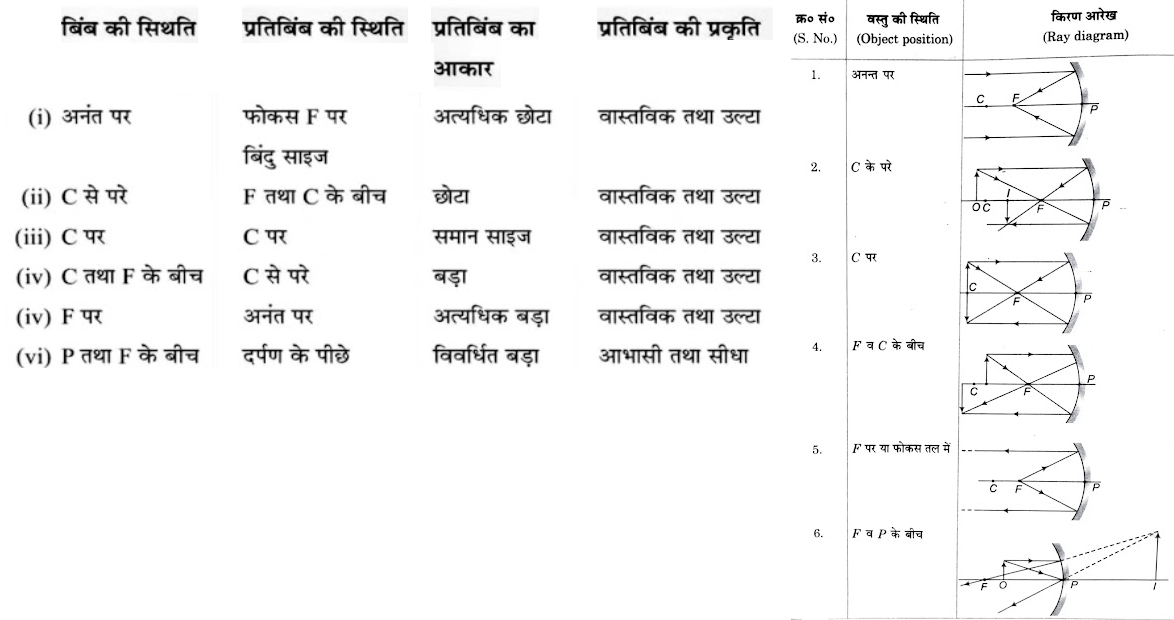
उत्तल दर्पण के लिए

◊ गोलीय दर्पण का उपयोग

(a) हजामत बनाने का दर्पण- अवतल दर्पण

हजामत बनाने वाले दर्पण में अवतल दर्पण का प्रयोग इसलिए किया जाता है क्योंकि जब अवतल दर्पण को वस्तु के बहुत निकट रखा जाता है तो आवर्धित तथा आभासी प्रतिबिम्ब प्राप्त होता है।

(b) पश्चदृश्य दर्पण – उत्तल दर्पण

उत्तल दर्पण का उपयोग वाहनों में पश्च-दृश्य दर्पण के रूप में किया जाता है क्योंकि यह एक छोटा सीधा प्रतिबिंब बनाता है। तो यह देखने का एक व्यापक क्षेत्र देता है, जो चालक को उसके पीछे के अधिकांश यातायात को देखने की अनुमति देता है।

जब सर्चलाइट के बल्ब को अवतल दर्पण के फोकस पर रखा जाता है, तो यह प्रकाश को लंबी दूरी (अनंत) तक फैलने देता है और वे लगभग समानांतर होते हैं

ग़लतफ़हमी :-

यदि किसी दर्पण या लेंस को आधे भाग पर काला कर दिया जाए तो आधा प्रतिबिम्ब बनेगा।
(उत्तर- नहीं, पूर्ण प्रतिबिम्ब बनता है केवल तीव्रता कम होती है)
यदि दर्पण में छेद हो जाए तो प्रतिबिम्ब में भी छेद दिखाई देने लगता है।
(उत्तर- पिछले जैसा ही)
दर्पण सूत्र का उपयोग किसी भी दर्पण के लिए किया जाता है
(नहीं, दर्पण सूत्र का उपयोग केवल उपाक्षीय किरणों (छोटा द्वारक) के लिए किया जाता है

Questions

reflection (Hindi ) – set 1 reflection (Hindi) – set2