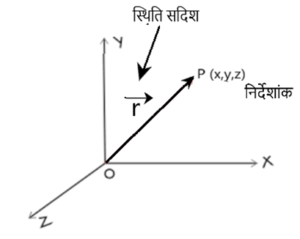
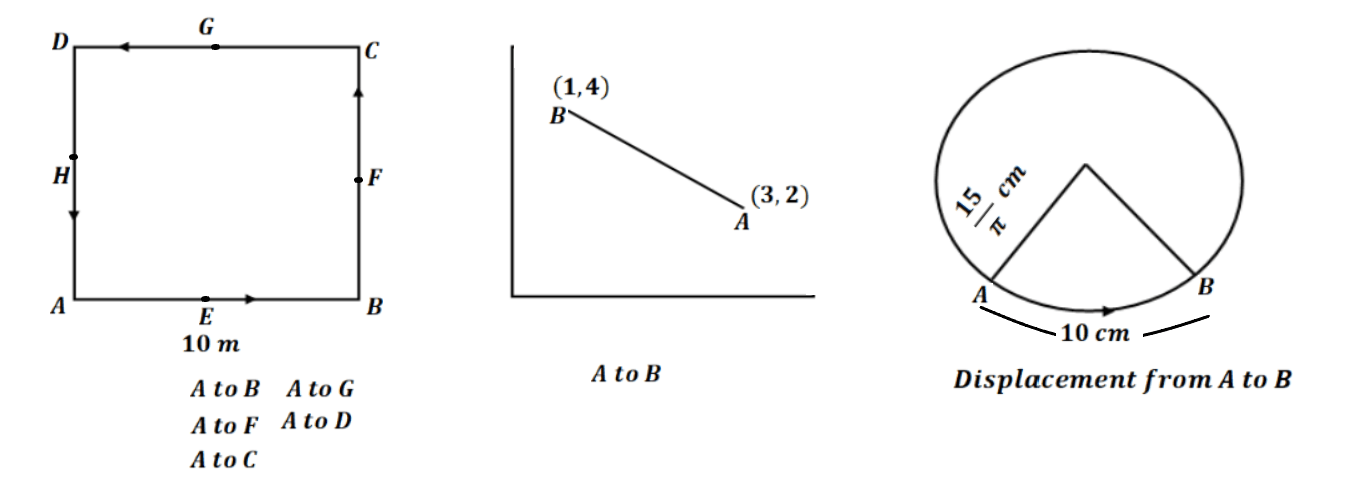निर्देश तंत्र (Frame of Reference) :-
किसी कण की स्थिति अथवा किसी घटना के स्थान को ठीक ठीक प्रदर्शित करने के लिए तीन परस्पर लंबवत अक्षों के समुच्चय को निर्देश तंत्र कहते है। किसी पिंड की स्थिति को निर्देशांक(co-ordinate) या स्थिति सदिश(position vector) द्वारा दिखाया जाता है।
निर्देश तंत्र दो प्रकार के होते है (1) जड़त्वीय निर्देश तंत्र और (2) अजड़त्वीय निर्देश तंत्र
जड़त्वीय निर्देश तंत्र(Intertial frame of reference)
वे निर्देश तंत्र जिस पर कोई नेट बाह्य बल कार्य नहीं करता है , उसे जड़त्वीय निर्देश तंत्र कहते है। इस निर्देश तंत्र में न्यूटन के गति विषयक नियम लागु होते है ।
कोई भी निर्देश तंत्र जो बिरमावस्था में हो या समरूप गति में हो अर्थात जिसमे त्वरण शुन्य हो , जड़त्वीय निर्देश तंत्र होता है।
व्यवहार में पृथ्वी से जुड़ा कोई भी निर्देश तंत्र एक जड़त्वीय निर्देश तंत्र होता है।
अजड़त्वीय निर्देश तंत्र(Non inertial frame of reference)
वे निर्देश तंत्र जिस पर कोई नेट बाह्य बल कार्य करता है , उसे अजड़त्वीय निर्देश तंत्र कहते है। इस निर्देश तंत्र में न्यूटन के गति विषयक नियम लागु नहीं होते है। यह निर्देश तंत्र हमेशा त्वरित अवस्था में होता है।
विरामावस्था (Rest):-
समय के साथ किसी निर्देश तंत्र के सापेक्ष किसी पिंड की स्थिति का नहीं बदलना पिंड का विरामावस्था कहलाती है।
गति(Motion):-
समय के साथ किसी निर्देश तंत्र के सापेक्ष किसी पिंड की स्थिति का निरंतर बदलना गति कहलाती है।
जैसे – सड़क पर चलती कार , उड़ता हुआ पंक्षी इत्यादि
स्थिति के परिवर्तन के अनुसार गति के तीन प्रकार होते है।
एक विमीय गति (One dimensional motion):- इस गति में समय के साथ केवल एक निर्देशांक बदलता है। जैसे – रेलगाड़ी का सीधी पटरी पर चलना।
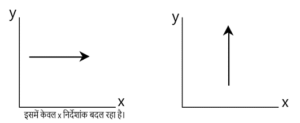
द्वि विमीय गति (Two dimensional motion) :- इस गति में समय के साथ केवल दो निर्देशांक बदलता है। जैसे – प्रक्षेप्य गति , वृतीय गति इत्यादि
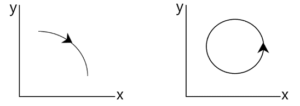
त्रि विमीय गति (Three dimensional motion) :- इस गति में समय के साथ तीनो निर्देशांक बदलता है। जैसे – आकाश में उड़ती हुई चिड़ियाँ की गति ।
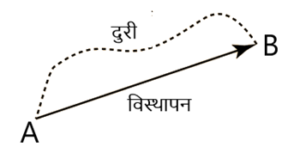
दुरी (Distance) :-
किसी वस्तु द्वारा तय किये गए मार्ग की लम्बाई को उस वस्तु द्वारा तय की गई दुरी कहते है। यह एक अदिश राशि है , तथा इसका S.I मात्रक मीटर(m) होता है।
विस्थापन (Displacement):-
किसी वस्तु की प्रारंभिक और अंतिम स्थितियों के बिच की न्यूनतम दुरी को विस्थापन कहते है। यह एक सदिश राशि है तथा इसका S.I मात्रक मीटर(m) होता है।
NOTE:-
- एक विमीय गति के लिए दुरी तथा विस्थापन का परिमाण समान होता है।
- दुरी का परिमाण कभी भी शून्य नहीं होता है लेकिन एक पूर्ण पथ ( जिसमे प्रारंभिक तथा अंतिम स्थिति एक हो ) का विस्थापन हमेशा शून्य होता है।
- दुरी हमेशा +ve होती है लेकिन विस्थापन +ve , -ve तथा शून्य हो सकता है।
- यदि किसी वस्तु का विस्थापन A से B तक हुआ है तो |
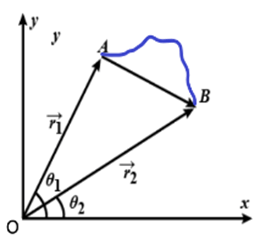
चित्र के अनुसार
(स्थिति सदिश का अंतर )
दुरी तथा विस्थापन सम्बंधित प्रश्न(1) दिए गए चित्र में वस्तु का दुरी तथा विस्थापन का मान ज्ञात करें ।
(2) निम्न दिए गए बिंदुओं का स्थिति सदिश ( परिमाण तथा दिशा ) ज्ञात करे । (3,4), (4,3), (4,4), (-3,-3), (1, √3), (√3,1), (-1,√3),(√3,-1), (-√3,-1), (-2,-2) (3) निचे दिए गए दो बिंदु युग्म का विस्थापन सदिश ( परिमाण तथा दिशा ) ज्ञात करें ।
|
चाल
किसी अनिश्चित दिशा में वस्तु के स्थिति में परिवर्तन की दर को वस्तु की चाल कहते है अर्थात वस्तु की दुरी तथा समय के अनुपात को वस्तु की चाल कहते है ।
औसत चाल (Average Speed)
किसी वस्तु द्वारा तय की गई कुल दूरी तथा उसमे लगा समय के अनुपात को उस वस्तु का औसत चाल कहते है।
अर्थात , औसत चाल = कुल दुरी / कुल समय
यह एक अदिश राशि है तथा इसका S.I मात्रक मीटर /सेकंड (m/s) होता है। इसका विमीय सूत्र [M0LT-1] है।
तात्क्षणिक /क्षणिक चाल (चाल ) (Instantaneous Speed/ Speed)
किसी दिए हुए क्षण पर किसी वस्तु की चाल को उसकी क्षणिक चाल कहते है।
अर्थात,
कार की चालमापी (speedometer) उसकी ताक्षणिक चाल को प्रदर्शित करता है।
वेग
किसी निश्चित दिशा में वस्तु के स्थिति में परिवर्तन की दर को वस्तु का वेग कहते है अर्थात वस्तु का विस्थापन तथा समय के अनुपात को वस्तु का वेग कहते है ।
औसत वेग (Average Velocity)
किसी वस्तु द्वारा तय की गई कुल विस्थापन तथा उसमे लगा समय के अनुपात को उस वस्तु का औसत वेग कहते है।
अर्थात औसत वेग = कुल विस्थापन / कुल समय
यह एक सदिश राशि है तथा इसका S.I मात्रक मीटर /सेकंड (m/s) होता है। इसका विमीय सूत्र [M0LT-1] है।
तात्क्षणिक /क्षणिक वेग (वेग ) (Instantaneous Velocity/ Velocity)
किसी दिए हुए क्षण पर किसी वस्तु की वेग को उसकी क्षणिक वेग कहते है।
अर्थात
NOTE:-
- एक विमीय गति में औसत चाल तथा औसत वेग का मान समान रहता है।
- एक पूर्ण पथ के लिए औसत वेग का मान शून्य होता है।
- किसी भी प्रकार के गति के लिए किसी क्षण वस्तु का क्षणिक चाल तथा क्षणिक वेग का परिमाण हमेशा समान रहता है।
- यदि कोई वस्तु समान चाल से चलती हुई अपनी दिशा को बदलती है तो उसके वेग में परिवर्तन होता है , क्योंकि दिशा में परिवर्तन हुआ है।
औसत चाल, क्षणिक चाल , औसत वेग तथा क्षणिक वेग सम्बंधित प्रश्न(1) एक बस देवघर से रांची 320 km सड़क मार्ग से 8 घंटे में तय करती है जबकि एक हवाईजहाज 260 km वायुमार्ग से 30 min में तय करके पहुँचती है ।बस तथा हवाईजहाज का औसत चाल तथा औसत वेग ज्ञात करें । (2) जब एक व्यक्ति अपने घर से निकलता है तो अपने कार के मीटर स्क्रीन में 12352 km देखता है लेकिन जब वह 2 घंटे में वापस अपने घर पहुँचता है तो 12416 km देखता है । कार की औसत चाल तथा औसत वेग ज्ञात करें । (3) निम्न में प्रत्येक स्थिति में वस्तु की औसत चाल तथा औसत वेग ज्ञात करे जब वह बिंदु A से बिंदु B तक 2 sec में पहुँचता है
(4) एक टेबल घडी के मिनट की सुई की लम्बाई 4 सेमी है । मिनट की सुई की नोक का 6:00 a.m तथा 6:30 a.m के बीच औसत वेग ज्ञात कीजिए। (5) एक व्यक्ति जो x- अक्ष में चल रही है 25 मीटर चल कर रुक जाती है , फिर वह 10 मीटर वापस आकर रुक जाती है , पूरी यात्रा तय करने में वह 10 सेकंड का समय लगता है व्यक्ति का औसत चाल तथा औसत वेग ज्ञात करें । (6) एक कण x- अक्ष के अनुदिश इस प्रकार चलता है कि उसका x-coordinate समय के साथ इस प्रकार बदल रही है (a) 3 सेकेंड से 5 सेकेंड के बीच कण का विस्थापन (33.6 m) (7) x-अक्ष के अनुदिश गति कर रहे किसी कण का मीटर में विस्थापन इस प्रकार दिया जाता है (8) x-अक्ष के अनुदिश गति कर रहे किसी कण का मीटर में विस्थापन इस प्रकार दिया जाता है (9) x-अक्ष के अनुदिश गति कर रहे किसी कण का मीटर में विस्थापन इस प्रकार दिया जाता है (10) एक प्रोटोन x- अक्ष के अनुदिश इस समीकरण के अनुसार चल रहा है (11) विरामावस्था से शुरू होने वाले इलेक्ट्रान का वेग समय के साथ इस प्रकार बदल रहा है v=kt, जहाँ k= 2m/s² और . पहले 3sec में इलेक्ट्रान द्वारा तय की गई दुरी क्या होगी ? (9 m) (12) सीधी सड़क पर चलती हुई कार कुल दुरी का एक तिहाई भाग 20 km/h तथा शेष 60 km/h से पूरी करती है । इसकी औसत चाल कितनी होगी । ( 36 km/h) |
एक समान गति / समरूप गति / समरूप वेग (Uniform motion):-
जब किसी गतिमान पिण्ड का विस्थापन समान समय अन्तराल में समान रहता है तो उस पिण्ड के गति को एकसमान गति कहते है।
इसमें वस्तु के वेग का मान तथा दिशा नियत(constant) रहती है। एकसमान गति में पिण्ड का औसत वेग तथा क्षणिक वेग समान रहता है।
अर्थात वेग=विस्थापन / समय
समरूप गति सम्बंधित प्रश्न(1) एक कार दो स्थानों के बीच की आधी दुरी 40 km/h तथा शेष 60 km/h की चाल से तय करती है । कार की औसत चाल क्या है ? (48 km/h) (2) एक कार कुल दुरी का 1/3 भाग 10 km/h, दूसरा 1/3 भाग 20 km/h तथा शेष भाग 60 km/h की चाल से तय करती है । कार की औसत चाल ज्ञात करें । (18 km/h) (3) एक कार सीधी सड़क पर 15 min तक 30 km/h की चाल से , अगला 15 min तक 40 km/h की चाल से तथा अंतिम 15 min तक 60 km/h की चाल से तय करती है । कार का औसत चाल कितनी होगी । (4) एक ट्रेन 100 मीटर लम्बा है तथा 45 km/h की चाल से चल रही है , 1 km लम्बे पूल को पार करने में कितना समय लगेगा । (88 सेकेण्ड) (5) एक कार सीधी सड़क पर चल रही है । वह अपने मार्ग में आधा समय 50 km/h तथा शेष आधा समय 60 km/h की चाल से तय करती है, कार का औसत चाल ज्ञात करें । (55 km/h) (6) 60 km लम्बे मार्ग में एक ट्रेन, पहला 30 km , 30 km/h की समरूप चाल से तय करती है । अगला 30 km वह किस चाल से तय करेगी की ट्रेन का कुल औसत चाल 40 km/h हो जाये । (7) निचे दिए गए टेबल में एक वस्तु की चाल अलग अलग समय अंतराल में दी गई है , वस्तु का औसत चाल ज्ञात करें । t(s) v(m/s) (8) एक लड़का अपने घर से बाज़ार तक एक सीधी सड़क पर 2 किलोमीटर दूर 4km/h की चाल से चलता है । बाजार को बंद पाकर वह तुरंत ही अपने घर की ओर 6 km/h की चाल से वापस लौटता है । गणना कीजिये (a) औसत चाल (b) औसत वेग का परिमाण (c) 0 से 30 मिनट तथा 0 से 40 मिनट के समयांतराल में लड़के की औसत वेग की गणना करें ।(4।8 km/h, 0, 4km/h, 4.5 km/h) (9) एक चोर जीप में 10 m/s के वेग से भाग रहा है । एक पुलिस की गाड़ी 12 m/s के वेग से उसका पीछा कर रही है । प्रारम्भ में पुलिस की गाड़ी जीप से 80 मीटर पीछे है । चोर को पकड़ने में पुलिस को कितना समय लगेगा ।( 40 सेकंड ) (10) एक बस 10 m/s के वेग से चल रही है । एक कार 60 सेकंड में बस से आगे निकलना चाहता है । कार का वेग कितना होना चाहिए जिससे वह बस से आगे निकल जाये । बस कार से 1 किमी आगे है । (26.67 m/s) (11) एक 80 मीटर लम्बी ट्रेन 30 m/s के वेग से एक अन्य 100 मीटर लम्बी ट्रेन से आगे निकलती है । दूसरी ट्रेन की चाल 20 m/s है । पहली ट्रेन द्वारा दूसरी ट्रेन से आगे निकलने में लगा समय ज्ञात कीजिये । ( 18 सेकंड )
|
त्वरण (Acceleration)
जब किसी गतिशील वस्तु के वेग में परिवर्तन होता है तो उसकी गति त्वरित गति (Accelerated motion) कहलाती है। वेग में परिवर्तन वेग के परिमाण में अथवा दिशा में अथवा दोनों में हो सकता है। किसी वस्तु के वेग में परिवर्तन की दर को उस वस्तु का त्वरण कहते है।
NOTE:-
(1) यदि वस्तु के वेग का परिमाण समय के साथ बढ़ रहा हो , तो वस्तु का त्वरण +ve होता है। यदि वस्तु के वेग का मान समय के साथ घट रहा हो , तो वस्तु का त्वरण -ve होता है। -ve त्वरण को मंदन (Retardation) भी कहते है।
(2) यदि वस्तु का त्वरण वेग की दिशा में होगा तो वस्तु का वेग बढ़ेगा तथा यदि त्वरण वेग की दिशा के विपरीत होगा तो वस्तु का वेग घटेगा ।
औसत त्वरण (Average acceleration)
किसी वस्तु के वेग में परिवर्तन तथा उसमे लगा समय के अनुपात को औसत त्वरण कहते है।
अर्थात औसत त्वरण = वेग में परिवर्तन / समय अंतराल
यह एक सदिश राशि है तथा इसका S.I मात्रक m/s2होता है तथा विमीय सूत्र [M0LT-2 ]होता है।
क्षणिक त्वरण/त्वरण (Instantaneous Acceleration/Acceleration)
किसी दिए हुए क्षण पर किसी वस्तु के त्वरण को उसका क्षणिक त्वरण कहते है।
अर्थात
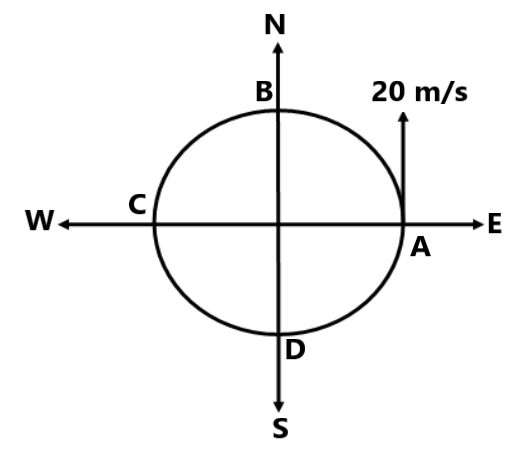
औसत त्वरण तथा क्षणिक त्वरण सम्बंधित प्रश्न(1) एक कार जो 20 m/s की चाल से सीधी सड़क पर चल रही है एक ट्रक को ओवरटेक करती है , जिसके लिए वह अपनी चाल को 2 sec में 25 m/s कर लेती है । कार का औसत त्वरण ज्ञात करें । (2) यदि एक कार उत्तर दिशा में 36 किमी/घंटा के वेग से चलती है। यह 10 सेकंड में अपनी गति बिना बदले बायीं ओर मुड़ जाती है। औसत त्वरण का परिमाण और दिशा ज्ञात कीजिए। (3) एक कार 20 मीटर/सेकेंड की नियत चाल से एक वृत्ताकार पथ पर चल रही है।औसत त्वरण ज्ञात कीजिए जब कार चलती है।
(a) A to B in 2 sec (b) A to C in 4 sec (c) A to D in 6 sec (d) A to A in 8 sec (4) x-अक्ष के अनुदिश गति कर रहे किसी कण का मीटर में विस्थापन इस प्रकार दिया जाता है x=18t+15t² (all in S.I) ज्ञात करें (a) t=2 sec पर कण का वेग (5) x-अक्ष के अनुदिश गति कर रहे किसी कण का मीटर में विस्थापन इस प्रकार है x=3+8t+7t² . t=2sec में कण का वेग तथा त्वरण ज्ञात करें । (6) किसी कण की स्थिति समय के अनुसार इस प्रकार बदल रही है x=5t³ . समय के function के रूप में कण का वेग और त्वरण ज्ञात कीजिए। (7) किसी कण का वेग समय के साथ इस प्रकार बदल रहा है v=2t²+5 ( सभी मात्रक S.I में है ) . ज्ञात करें (a) 2 sec से 4 sec समय अंतराल के दौरान कण के वेग में परिवर्तन (8) x-अक्ष के अनुदिश गति कर रहे किसी कण का मीटर में विस्थापन इस प्रकार है x=180t + 50t² , ज्ञात करें (a) कण का प्रारंभिक वेग (9) एक वस्तु जो सीधी रेखा पर चल रही है , उसका त्वरण समय के साथ इस प्रकार बदल रहा है a=3t²+2t+2. यदि वस्तु 2 m/s से चलना प्रारम्भ करती है तो 2 sec बाद वस्तु की चाल कितनी होगी। (10) कोई कण जो सीधी सड़क पर चल रही है , दिया हुआ है a=3t², यदि कण का प्रारंभिक वेग 2 m/s है तो समय के साथ वेग का समीकरण ज्ञात करें । (11) यदि |
एक समान त्वरित गति( Uniformly Accelerated Motion)
जब किसी गतिमान वस्तु के वेग में परिवर्तन समान समय अन्तराल में समान होता है तो उस वस्तु के गति को एक समान त्वरित गति कहते है। चूँकि वस्तु का त्वरण नियत होता है , अतः किसी भी क्षण पर वस्तु में त्वरण , पिण्ड के औसत त्वरण के बराबर ही होगा।
नियत त्वरण के अन्तर्गत एक विमीय गति के लिए समीकरण (equation)
जब कोई वस्तु नियत त्वरण से एक सरल रेखीय पथ पर गतिमान होती है , तब उसके विस्थापन , वेग ,त्वरण तथा समय के पारस्परिक सम्बन्धो को कुछ समीकरणों द्वारा व्यक्त किया जाता है , इन समीकरणों को गति का समीकरण कहते है।
माना की एक वस्तु u वेग से ऋजुरेखीय/ सरल रेखीय / एक विमीय पथ पर नियत त्वरण a से चलना प्रारम्भ करती है। जिसके कारण t समय बाद वस्तु का वेग v हो जाता है तथा इस समय अन्तराल में वस्तु s विस्थापित हो जाती है।
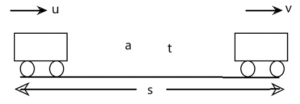
हम जानते है किसी क्षण वस्तु का त्वरण होगा
दोनों तरफ integration करने पर
यह गति का पहला समीकरण है।
उसी प्रकार किसी भी क्षण वस्तु का वेग होगा
दोनों तरफ integration करने पर
यह गति का दूसरा समीकरण है।
हम जानते है की किसी भी क्षण
दोनों तरफ integration करने पर
यह गति का तीसरा नियम है
वस्तु का nवे सेकंड में विस्थापन:-
यदि किसी वस्तु का n sec में विस्थापन Sn हो और (n-1) sec में विस्थापन Sn-1 हो तो nवे sec में विस्थापन (Sn-Sn-1) होगा |
अर्थात nवे sec में विस्थापन
गुरुत्वाकर्षण के अंतर्गत वस्तु की गति
जब किसी वस्तु को पृथ्वी के गुरुत्वाकर्षण के अधीन छोड़ा जाता है तो उसके वेग में परिवर्तन होता है । यह परिवर्तन पृथ्वी द्वारा वस्तु पर लगाए गए त्वरण ( बल ) के कारण होता है । इस त्वरण को गुरुत्वीय त्वरण कहते है, इसे g द्वारा सूचित किया जाता है ,जिसके दिशा हमेशा ऊर्ध्वाधर निचे की ओर होती है , पृथ्वी के सतह के निकट इसका मान 9.8 m/s² होता है ।
जब कोई वस्तु स्वतंत्र रूप से निचे गिरती है तो उसका वेग बढ़ता है अतः g का मान +ve होगा उसी प्रकार जब कोई वस्तु को ऊर्ध्वाधर ऊपर की ओर फेंका जाता है तो उसका वेग घटता है अतः g का मान -ve होगा ।
NOTE:-
यदि g का मान सदिश के रूप में लिया जाता है तो वह हमेशा -ve होगा ।
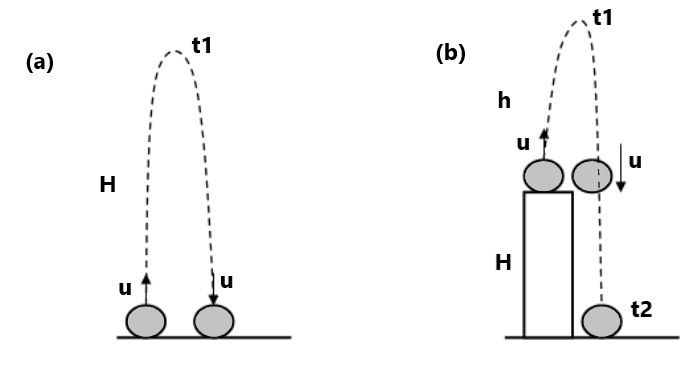
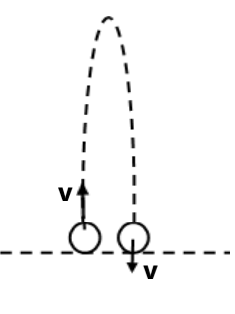
यदि किसी वस्तु को ऊर्ध्वाधर ऊपर की ओर फेंका जाता है तो जितना समय ऊपर जाने में लगेगा उतना समय निचे आने में लगेगा । ऊपर जाने में लगा समय = निचे आने में लगा समय = u/g
एक सामान त्वरित गति सम्बंधित प्रश्न(1) एक पिंड 20 m/s के वेग से चलना प्रारम्भ करता है । यदि उसका त्वरण 2 m/s2 हो तो (a) 10 सेकंड बाद पिंड का वेग (b) 5 सेकंड में पिंड द्वारा तय की दुरी ज्ञात करें । ( 40 m/s , 125 मीटर ) (2) एक पिंड विराम से चलना प्रारम्भ करती है तथा 5 सेकंड में 12 m/s का वेग प्राप्त कर लेता है । वस्तु का त्वरण तथा तय की गई दुरी ज्ञात कीजिये । ( 2.4 m/s², 30 मीटर ) (3) एक जेट विमान 3 m/s² त्वरण के साथ विराम अवस्था से चलना प्रारम्भ करती है , और उड़ने से पहले 35 सेकंड तक दौड़ता है । हवाई पट्टी की न्यूनतम लम्बाई क्या है तथा विमान को उड़ने के समय वेग क्या होगा । (1837.5 मीटर , 105 m/s ) (4) 30 m/s की चाल से गतिमान एक कार में ब्रेक लगाए जाते है । इसका वेग 5 सेकंड में 20 m/s तक कम हो जाता है । ब्रेक द्वारा उत्पन्न मंदन ज्ञात कीजिये तथा इन 5 सेकंड में तय की गई दुरी भी ज्ञात कीजिये । (- 2m/s², 125 मीटर ) (5) 40 km/h की चाल से गतिमान एक कार ब्रेक लगाने पर 2 मीटर दूर चलकर रुक जाती है । यदि यही कार 80 km/h की चाल से गतिमान हो तो ब्रेक लगाने पर कितनी दूर पर रुक जाएगी । (8 मीटर ) (6) एक बस 30 km/h के वेग से चल रही है । ब्रेक लगाने पर वह 10 मीटर चलकर रुकने में कितना समय लगेगा । (2.4 second) (7) 60 km/h की चाल से जा रहा मोटर चालक यकायक अपने से 100 मीटर आगे सड़क पर पड़े पत्थर को देखता है । वह तुरंत ब्रेक लगता है जिससे 15 m/s² का मंदन उत्पन्न होता है । मोटर रोकने में कितना समय लगेगा ? क्या वह पत्थर से टकराता है ? (10/9 सेकंड , नहीं ) (8) सीधे राजमार्ग पर एक कार 126 km/h की चाल से चल रही है । इसे ब्रेक लगाकर 200 मीटर की दुरी पर रोक दिया जाता है । यदि कार का मंदन समरूप हो तो कार को रुकने में कितना समय लगेगा । (11.44 सेकंड ) (9) एक वस्तु विरामावस्था से चलना प्रारम्भ करती है जिसका त्वरण 10 m/s² है , 5 वे सेकंड में वह कितनी दुरी तय करेगी । (10) एक वस्तु विरामावस्था से चलना प्रारम्भ करती है तथा गति के 10 वे सेकंड में 1.71 मीटर दुरी तय करती है । वस्तु का त्वरण ज्ञात करें । ( 0.18 m/s²) (11) एक पिंड विरामावस्था से चलना प्रारम्भ करके गति के आठवें सेकंड में 1.2 मीटर की दुरी तय करता है । पिंड में त्वरण का परिणाम कितना होगा । ( 0.16 m/s²) (12) एक पिंड ऊपर की ओर 100 m/s के वेग से फेंका जाता है । यह कितने समय में वापस लौट जायेगा । ( 20 सेकंड ) (13) एक गेंद 10 m/s के वेग से ऊर्ध्वाधर ऊपर की ओर फेंकी जाती है (a) गेंद कितनी ऊंचाई तक जाएगी (b) कितने समय बाद वह लौटा प्रारम्भ करेगी (c) पृथ्वी पर पहुँचने पर गेंद का वेग क्या होगा ? ( g=10 m/s²) ( 5 मीटर , 1 सेकंड , 10 m/s) (14) एक गेंद को वायु की अनुपस्थिति में 29.4 m/s के वेग से ऊपर की ओर फेंका जाता है । (a) गेंद की ऊपर की ओर गति के दौरान त्वरण की दिशा बतलाइये (b) उच्चत्तम बिंदु पर गेंद का वेग और त्वरण क्या है ? (c) गेंद कितनी ऊंचाई तक जाती है (d) गेंद को ज़मीन तक पहुँचने में कितना समय लगेगा । (44.1 मीटर , 6 सेकंड ) (15) एक लड़का नदी के पुल पर खड़ा है । वह 4.9 m/s के वेग से एक पत्थर ऊर्ध्वाधर ऊपर की ओर फेंकता है जो 3 सेकंड पश्चात् नदी के जल से टकराता है । पुल से नदी की गहराई ज्ञात कीजिये । ( 29.4 मीटर ) (16) एक पत्थर को 100 मीटर ऊंचाई वाली मीनार की चोटी से गिराया जाता है । पत्थर ज़मीन पर पड़ी बालू में 2 मीटर तक घुस जाता है । पत्थर के मंदन की गणना कीजिये । (-490 m/s²) (17) एक व्यक्ति गेंद को ऊर्ध्वाधर ऊपर की ओर फेंकता है तो यह गेंद 20 मीटर ऊंचाई तक जाती है और उसके हांथों में लौट आती है । गेंद का प्रारंभिक वेग क्या था , तथा यह वायु में कितने समय तक रही ? (g=10 m/s²) ( 20 m/s , 4 सेकंड ) (18) एक गुब्बारा जो की 12 m/s के वेग से ऊपर की ओर जा रहा है , किसी क्षण पृथ्वी से 65 मीटर की ऊंचाई पर है । ठीक इसी क्षण इससे एक पैकेट छोड़ा जाता है । पैकेट को पृथ्वी तक पहुँचने में कितना समय लगेगा ? ( 5 सेकंड ) (19) एक छातादारी सैनिक हवाई जहाज से कूदता है । जब वह मुक्त रूप से 40 मीटर गिर चुकता है, तब उसकी छतरी खुलती है । अब वह 2 m/s² के मंदन से गिरता है तथा पृथ्वी पर 3 m/s के वेग से पहुँचता है । हवाई जहाज कितनी ऊंचाई पर था? छाता दारी कितने देर वायु में रहा ? (234 मीटर , 15 सेकंड ) (20) एक गुब्बारा ऊर्ध्वाधर ऊपर चढ़ रहा है । जब यह पृथ्वी से 320 मीटर ऊपर तथा इस क्षण उसका वेग 49 m/s होता है , तो गुब्बारे से एक गेंद निचे गिरे जाती है । यदि वायु का प्रतिरोध नगण्य हो तो ज्ञात कीजिये (a) गेंद कितनी ऊंचाई तक जाएगी (b) गुब्बारे से गिरने के 5 सेकंड पश्चात् गेंद का वेग क्या होगा और कहाँ होगी ? (c) गेंद पृथ्वी पर कितने समय पश्चात् पहुंचेगी ( 442.5 मीटर , शून्य तथा पृथ्वी से 442.5 मीटर ऊपर , 14.5 सेकंड पश्चात् ) (21) एक गेंद को किसी मीनार की चोटी से 19.6 m/s की चाल से ऊर्ध्वाधर ऊपर की ओर फेंका जाता है और यह 6 सेकंड में पृथ्वी पर लौट आता है । मीनार की ऊंचाई ज्ञात कीजिये । (58.8 मीटर ) (22) कोई खिलाडी एक गेंद को ऊपर की ओर 29 m/s के वेग से फेंकता है । (a) गेंद की ऊपर की ओर गति के दौरान त्वरण की दिशा क्या होगी (b) इसकी गति के उच्चतम बिंदु पर गेंद के वेग तथा त्वरण की दिशा क्या होंगे ? (c) गेंद के उच्चतम बिंदु पर स्थान तथा समय को x=0 तथा t=0, ऊर्ध्वाधर निचे की दिशा को x- अक्ष की +ve दिशा चुनिए और गेंद की ऊपर की ओर तथा निचे की ओर गति में हेंड की स्थिति , वेग तथा त्वरण के चिन्ह बताइये । (d) गेंद किस ऊंचाई तक जाती है तथा कितने समय बाद खिलाडी के हाथों में वापस लौट आती है । (d- 3 सेकंड ) |
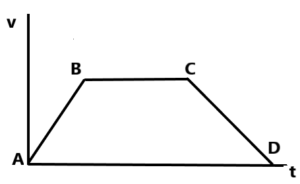
ग्राफ(Graph):-
ग्राफ को सुचना के सचित्र निरूपण के रूप में परिभाषित किया जाता है जो आश्रित(dependent variable) और स्वतंत्र चर (independent variable) के बीच संबंध को समझाने वाला एक द्वी – आयामी ( 2-Dimension) चित्र है।
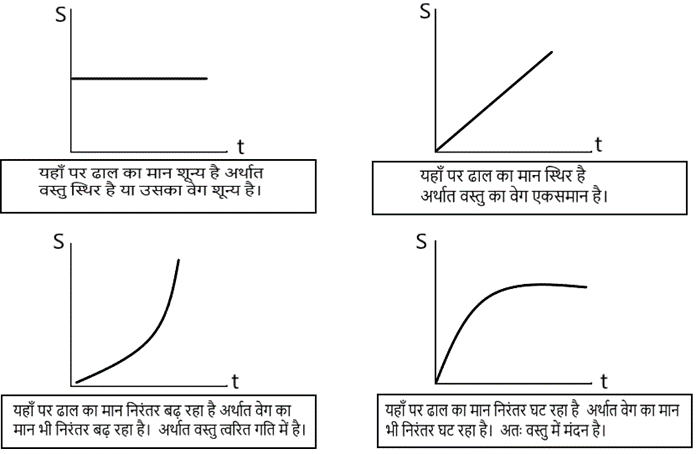
(1). विस्थापन – समय ग्राफ/ स्थिति समय ग्राफ( s-t graph)
इसमें साधारणतः विस्थापन को Y- अक्ष पर तथा समय को X- अक्ष पर दर्शाया जाता है।
हम जानते है की
अर्थात, (s-t) ग्राफ में किसी क्षण पर ढाल/slop (+ve X- अक्ष के साथ ) उस क्षण पर उस वस्तु का वेग प्रदर्शित करता है। s-t ग्राफ का ढाल जितना अधिक होगा वस्तु का वेग भी उतना अधिक होगा।
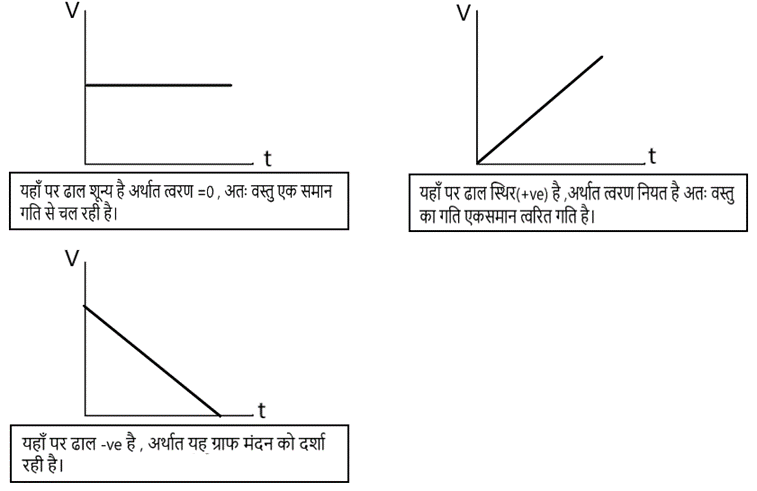
(2) वेग – समय ग्राफ (v-t graph)
इसमें साधारणतः वेग को Y- अक्ष पर तथा समय को कX- अक्ष पर दर्शाया जाता है।
हम जानते है की
अर्थात, किसी क्षण v-t ग्राफ में ढाल उस क्षण पर वस्तु का त्वरण को प्रदर्शित करता है। अर्थात v-t ग्राफ का ढाल जितना अधिक होगा वस्तु का त्वरण भी उतना ही अधिक होता है।
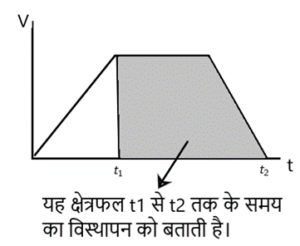
उसी प्रकार हम जानते है की
अर्थात v-t ग्राफ में , समय – अक्ष के बीच (t1 से t2 तक) घिरा हुआ क्षेत्रफल वस्तु के विस्थापन के बराबर होता है।
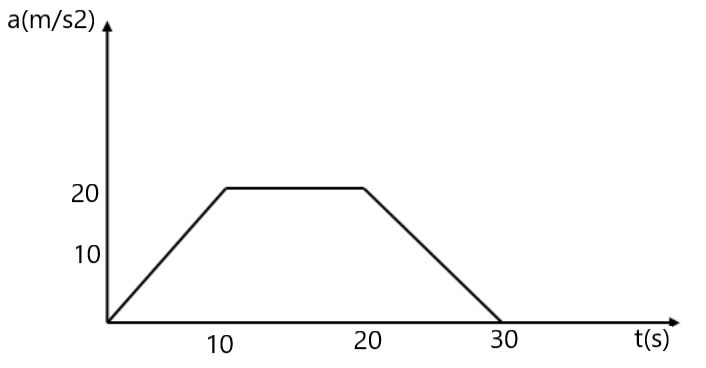
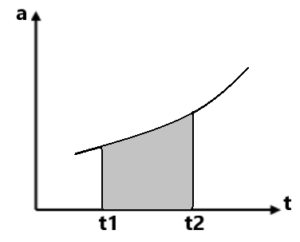
(3) त्वरण – समय ग्राफ (a-t graph)
हम जानते है की
अर्थात (a-t) ग्राफ में समय अक्ष में और
से घिरा क्षेत्रफल
और
समय में वेग के अंतर को दर्शाता है
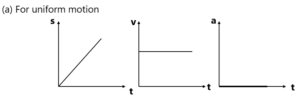
NOTE:-
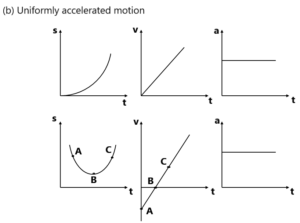
1. एक सामान गति ( समरूप गति ) के लिए
2. एक सामान त्वरित गति के लिए
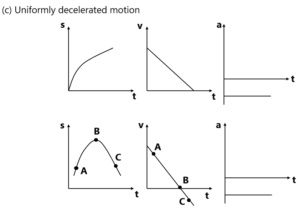
3. एकसमान मंदन गति के लिए
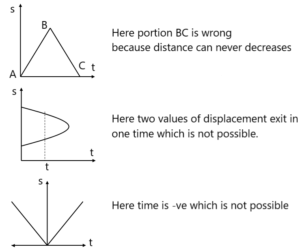
4. ऐसा ग्राफ संभव नहीं है
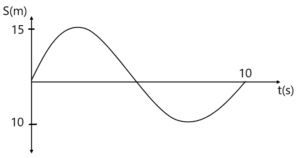
ग्राफ सम्बंधित प्रश्न1. 10 सेकंड में वस्तु द्वारा तय की गई दुरी तथा विस्थापन ज्ञात करें । ( 50 m)
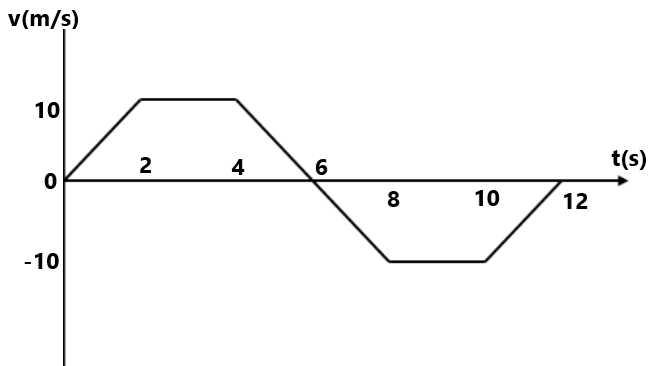
2. दिए गए ग्राफ से
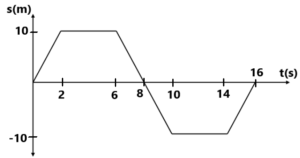
t=1 sec, 4 sec, 7 sec, 9 sec, 12 sec, 15 sec में वेग ज्ञात करें तथा दिए गए समयांतराल में औसत वेग ज्ञात करें t=o to 2 sec, t=0 to 4 sec, t=0 to 8 sec and t=0 to 16 sec. ( 5 m/s,0,-5 m/s, -5 m/s, 0, 5 m/s, 5 m/s, 2.5 m/s, -5/3 m/s 0) 3. किसी कण का s-t ग्राफ दिया हुआ है
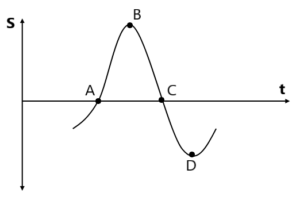
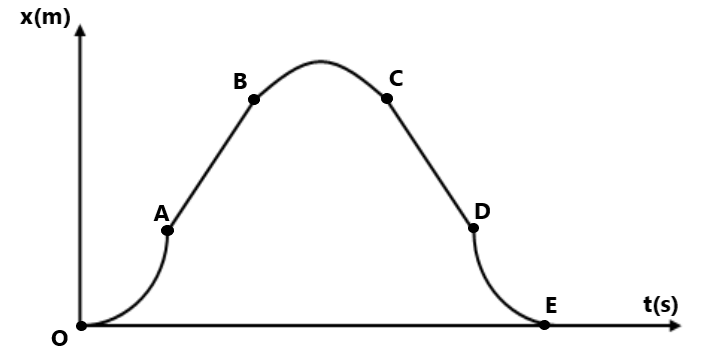
किस बिंदु पर वेग +ve, -ve तथा शून्य होगा । 4. किसी कण का x-t ग्राफ दिया हुआ है
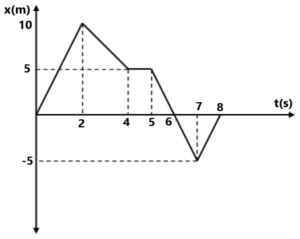
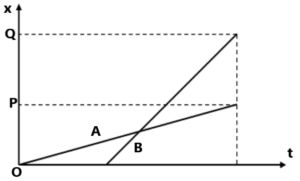
(a) समय अंतराल 0 to 2sec, 2 to 4 sec and 4 to 7 sec में कण का औसत वेग निकाले । (5 m/s, -2.5 m/s, -3.3 m/s) 5. दो बच्चे A व B अपने विद्यालय से लौटकर अपने-अपने घर मे क्रमशः P तथा Q को जा रहे हैं। उनके स्थिति-समय (x-t) ग्राफ चित्र में दिखाए गए हैं। नीचे लिखे कोष्ठकों में सही प्रविष्टियों को चुनिए
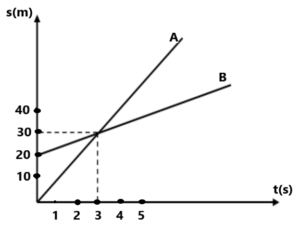
(a) B/A की तुलना में (A/B) विद्यालय से निकट रहता है। (6) दो कण का s-t ग्राफ निचे दिया गया है ।
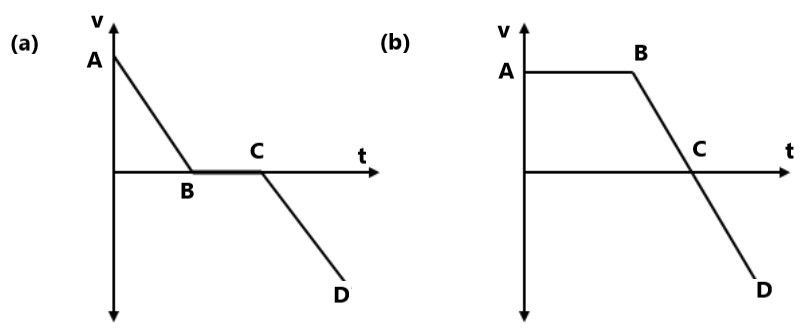
(a) प्रारंभिक में B , A से कितना आगे है । 7. दिए गए v-t ग्राफ में कण की गति का वर्णन करे ।
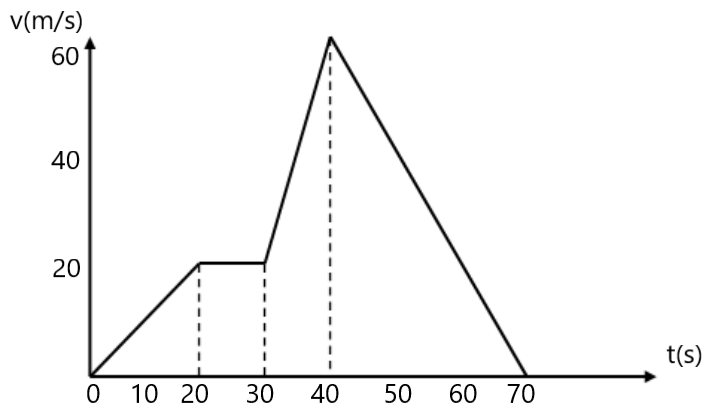
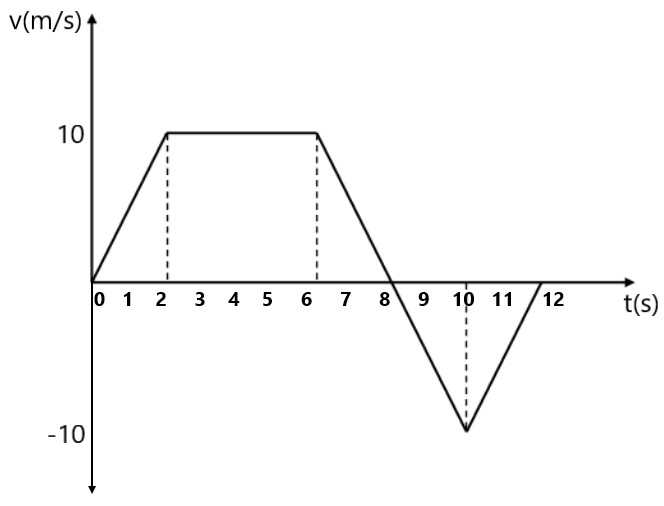
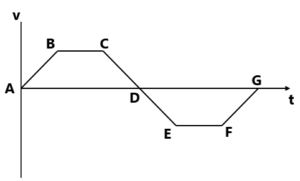
8. दिए गए ग्राफ में कण के गति का वर्णन करें , प्रत्येक समय अंतराल में कण का त्वरण ज्ञात करे , समय अंतराल 0-20 सेकंड , 0 से 30 सेकंड , 20 से 40 सेकंड तथा 30 से 70 सेकंड में औसत वेग ज्ञात करें ।
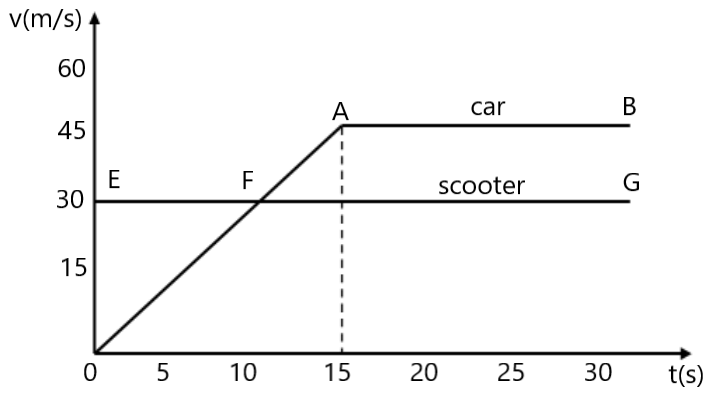
9. एक कार तथा स्कूटर एक बिंदु से चलना प्रारम्भ करती है , जिसका ग्राफ निचे दिया गया है ।
ज्ञात करें (a) 15 सेकंड में कार तथा स्कूटर द्वारा तय की गई दुरी । 10.
उपर्युक्त ग्राफ से वस्तु का औसत चाल तथा औसत वेग ज्ञात करें ।
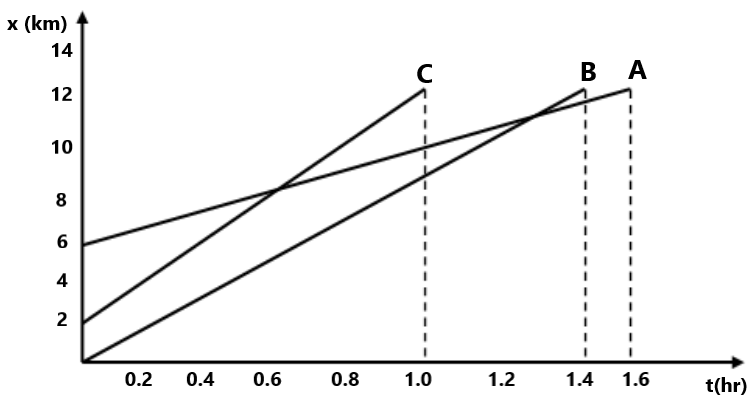
11. तीन कार A , B तथा C एक ही समय से चलना प्रारम्भ करती है जिसका x-t ग्राफ दिया हुआ है ।
(a) कौन सी कार की चाल सबसे अधिक है । (12) दो कण का x-t ग्राफ निचे दिया हुआ है
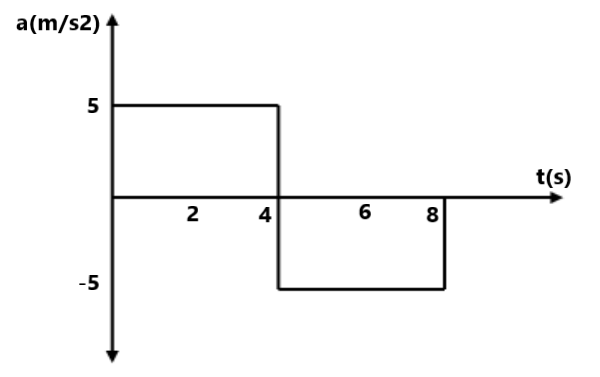
(a) किस समय दोनों कण एक ही स्थिति में होंगे ? (13). दिए गए ग्राफ में पहले 20 सेकंड में औसत त्वरण का मान ज्ञात करें ।
(14). एक वस्तु सीधी सड़क पर t=0 समय पर चलना प्रारम्भ करती है जिसका निचे (a-t) ग्राफ दिया गया है ।
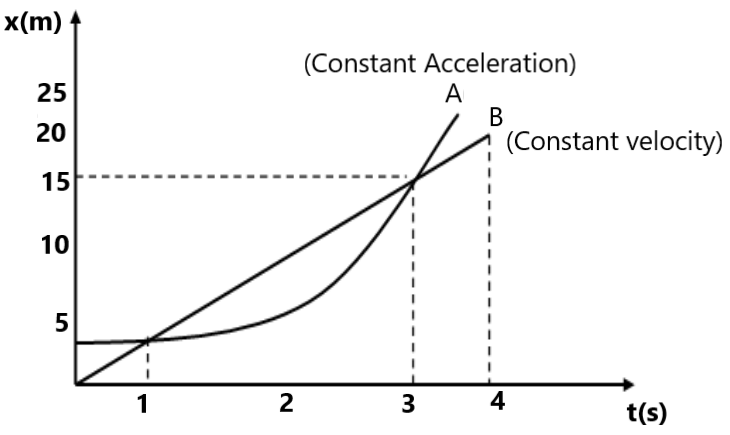
(a) (v-t) ग्राफ को खींचे । (15) दिए गए x-t ग्राफ से (v-t) तथा (a-t) ग्राफ खींचे ।
(16)
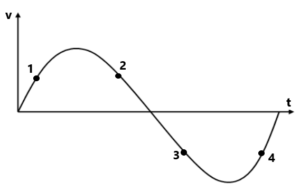
उपर्युक्त ग्राफ में प्रत्येक बिंदु पर वेग तथा त्वरण का चिन्ह बताएं । (17) दिए गए (v-t) ग्राफ से
ज्ञात करें (a) t=0 to 2 sec, t=0 to 4 sec and t=2 to 5 सेकंड में औसत त्वरण ज्ञात करें । 18. यदि u= 3m/s. तो दिए गए ग्राफ से t=4 sec में वस्तु का वेग कितना होगा ।
19. दिए गए (a-t) ग्राफ से (v-t) तथा (x-t) ग्राफ बनाइये ।
20. किसी ऊँचाई से गिराए गए किसी पिंड की गति का ग्राफ बनाइए। प्रारंभिक स्थिति मूल है और नीचे की दिशा +ve है। 21. निम्नलिखित स्थितियों के लिए (x-t), (v-t) तथा (a-t) ग्राफ बनाइये ।
|
आपेक्षिक वेग (Relative Velocity):-
हम जानते है की निरपेक्ष गति तथा निरपेक्ष विरामावस्था सम्भव नहीं है, प्रत्येक वस्तु की गति अथवा विरामावस्था किसी दूसरी वस्तु के सापेक्ष ही होती है। अर्थात एक वस्तु का वेग दूसरी वस्तु के सापेक्ष ही वस्तु का आपेक्षिक वेग कहलाती है।
B का वेग , A के सापेक्ष
अतः
हम यह लिख सकते है
जहाँ माना की G पृथ्वी को सम्बोधित कर रही है।
आपेक्षिक वेग सम्बंधित प्रश्न(1) 150 मीटर लम्बी एक ट्रेन 10 m/s की चाल से उत्तर दिशा में गतिमान है । एक तोता 5 m/s की चाल से ट्रेन के समान्तर दक्षिण दिशा में उड़ रहा है । तोते द्वारा ट्रेन को पार करने में कितना समय लगेगा । ( 10 सेकंड ) (2) दो रेलमार्ग पूर्व – पश्चिम दिशाओं में स्थित है । एक मार्ग पर एक रेलगाड़ी A 30 m/s कि चाल से पूर्व की ओर तथा दूसरे पर एक अन्य रेलगाड़ी B , 48 m/s की चाल से पश्चिम की ओर गतिमान है । ज्ञात कीजिये (a) A के सापेक्ष B की चाल (b) B के सापेक्ष जमीन की चाल ( 78 m/s, 48 m/s) (3) एक जैट हवाईजहाज 500 km/h की चाल से गतिमान है और इसमें से गैसें जहाज के सापेक्ष 1500 km/h की चाल से निकलती है । गैसों की जमीन पर खड़े दर्शक के सापेक्ष चाल ज्ञात करें । (1000 km/h) (4) 54 km/h की चाल से गतिमान ट्रेन की खिड़की के पास बैठा यात्री 36 km/h की चाल से विपरीत दिशा में गतिमान ट्रेन को देखता है । यदि ट्रेन की लम्बाई 150 मीटर हो , तो यात्री के सामने से यह ट्रेन कितने समय में गुजर जाएगी । (6 सेकंड ) |
लघु उत्तरीय प्रश्न(1) विस्थापन एवं दुरी में अंतर लिखिए । (2) चाल और वेग में अंतर लिखिए । (3) एकसमान गति से आप क्या समझते है । इसके लिए s-t तथा v-t ग्राफ खींचिए । (4) एकसमान त्वरित गति से आप क्या समझते है । इसके लिए s-t, v-t तथा a-t ग्राफ खींचिए । (5) एकसमान त्वरित गति के लिए s=ut+1/2 at² की स्थापना कीजिये । (6)क्या यह संभव है कि- (a) किसी वस्तु का औसत वेग शून्य हो, परन्तु औसत चाल शून्य न हो । क्या इसका विपरीत भी संभव है । (7) एक पिंड नियत त्वरण से विरामावस्था से चलना प्रारम्भ करके t सेकेंड में x दुरी तय करता है , अगले t सेकेंड में वह कितनी दुरी तय करेगा ? (3x) (8) एक पिंड को ऊर्ध्वाधर ऊपर कि ओर फेंका जाता है तथा वह लौट कर अपनी प्रारंभिक स्थिति में आ जाता है । इसकी गति का समय – वेग ग्राफ से प्रदर्शित कीजिये । (9) निचे दिए गए कथनों को ध्यान से पढ़िए और कारण बताते हुए एवं उद्धरण देते हुए बताइये की वे सत्य है या असत्य ? एक विमीय गति में किसी कण की : (a) किसी क्षण चाल शून्य होने पर भी उसका त्वरण अशून्य हो सकता है । (10) दिए गए ग्राफ का कौन सा भाग त्वरण , कौन सा भाग मंदन तथा कौन सा भाग एकसमान वेग को प्रदर्शित करता है ।
|
रिक्त स्थानों की पूर्ति करो(1) वेग परिवर्तन की समय दर को __________ कहते है । (2) गति के समीकरणों को वैज्ञानिक _________ ने ज्ञात किया था । (3) यदि किसी कण का विस्थापन समय के वर्ग के समानुपाती हो , तो पिंड का _________ एकसमान होगा । (4) स्वतंत्रता पूर्वक गिरती वस्तु का विस्थापन समीकरण h= ____________ होता है । (5) कोई v-t ग्राफ एक सीधी रेखा है जो समय अक्ष से कुछ कोण पर झुकी है । यह __________ गति को निरूपित करता है । (6) विरामावस्था से चलने वाले कण का एकसमान त्वरण 4 m/s² हो , तो 10 वे सेकंड में उसके द्वारा तय की गई दुरी __________ होगी । (7) किसी पिंड के वेग – समय ग्राफ में समय अक्ष के बीच गिरा क्षेत्रफल पिंड का ________ प्रदर्शित करता है । (8) किसी वस्तु का वेग , x-t ग्राफ में ________ के बराबर होता है । (9) -ve त्वरण को _________ कहते है । (10) किसी कण के s-t ग्राफ का ढाल कण का _________ प्रदर्शित करता है । (11) किसी कण का v-t ग्राफ का ढाल कण का ________ तथा समय अक्ष के बीच घिरा क्षेत्रफल कण का ________ प्रदर्शित करता है । (12) किसी कण का विस्थापन समीकरण s=3 + 5t + 10t² है । इस कण में त्वरण _________ है । (13) वेग और त्वरण में से पिंड की गति की दिशा निर्धारित करने वाली राशि __________ है । (14) दो गतिमान कणों के समय – विस्थापन ग्राफ एक ही पैमाने पर खींची गई है , जो x- अक्ष के साथ क्रमशः 30° एवं 60° का कोण बनती हुई सरल रेखाएं है । कणो के वेगों में ___________ का अनुपात है । |
दीर्घ उत्तरीय प्रश्न(1) किसी वस्तु द्वारा उसकी गति के n वें सेकेंड में चली गई दुरी के लिए व्यंजक प्राप्त करें । (2) गति के समीकरणों को समाकलन विधि से स्थापित कीजिये । |