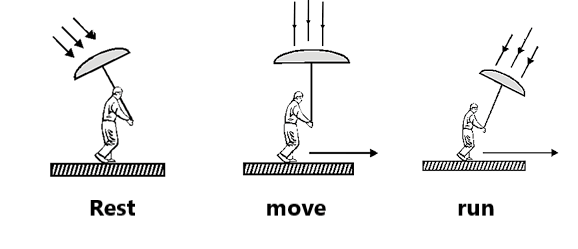
Both rest and motion are relative terms. A tree on the ground appears to be at rest for a person standing on the ground. The same tree appears to be in motion for an observer in a moving train. Two persons A and B sitting in a car at rest with each other. But both of them appear to be moving for a person at rest out the ground.
Suppose two trains are traveling in the same direction on two parallel tracks and one of them overtakes the other. The observer in the fast-moving train feels that it overtook the second one with less velocity whereas an observer on the ground feels that the velocity of the overtaking train is more than that of an observer in the train.
To understand such observation the concept of relative velocity was introduced. i.e. there is no meaning of motion without reference or observer. Generally, if a reference is not mentioned then we take the ground as a reference of motion.
i.e. we can say that relative motion is defined as the motion of an object w.r.t another observer.
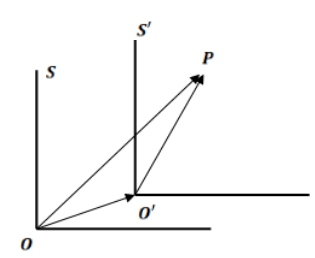
Here and
are the frame of reference
Now from fig
If we differentiate w.r.t, we get
Again if we differentiate w.r.t, we get
i.e. in general
| Relative Position
|
Relative velocity
Where |
Relative Acceleration
Where |
Equation of motion can be written as
and so on…….
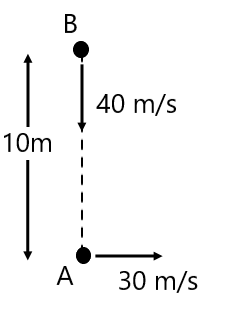
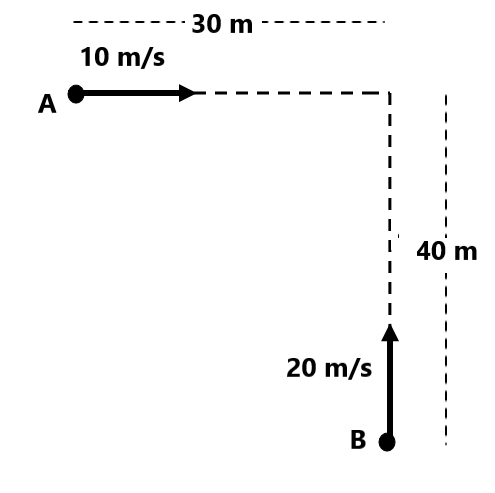
Numerical Questions for Relative Motion in 1 D(1) Find the relative velocity of B w.r.t A and find relative velocity of A w.r.t B (-5 m/s, 5 m/s)
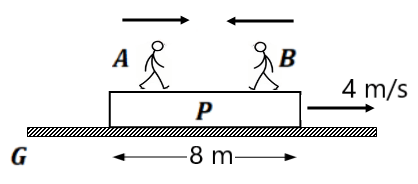
(2) Two parallel rail tracks run N-S. Train A moves north with a speed of 54 km/h and train B moves south with a speed of 90 km/h. A monkey running on the roof of train A against its motion with a velocity of 18 km/h w.r.t A. What is the velocity of the monkey (a) as observed by an observer on the ground (b) w.r.t train B (10 m/s north, 35 m/s north) (3) A police van moving on a highway with a speed of 30 km/h fires a bullet at a thief’s car speeding away in the same direction with a speed of 192 km/h. If the muzzle speed of the bullet is 150 m/s, at what speed does the bullet hit the thief’s car? ( Muzzle speed means the speed of bullet w.r.t van )(105 km/h) (4) A car travelling at 60 km/h overtake another car travelling at 42 km/h. Assuming each car to be 5 m long. Find the time taken during the overtake and the total road distance used for the overtake. ( 2 sec, 38.3 m) (5) Two men A and B are moving on a plank P which itself is moving on the ground G. The velocities of A, B, and P are given below.
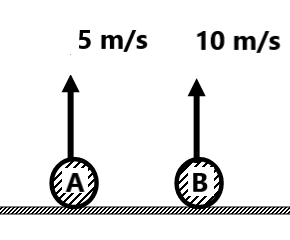
Find (a) (6) Two projectiles are thrown in the air. What will be the path of one as seen by the other? (Straight line with uniform motion) (7) Two trains 110 m and 90 m long are running in opposite directions with velocities of 36 km/h and 54 km/h. Find the time taken by the two trains to completely cross each other. (8 sec) (8) Two cars A and B are moving on straight parallel paths with speeds of 36 km/h and 72 km/h respectively starting from the same point in the same direction. After 20 min how much is behind car A from car B? ( 12 km) (9) A train 200 m long is moving with a velocity of 72 km/h. Find the time taken by the train to cross the bridge 1 km long. ( 60 sec) (10) A and B are thrown vertically upward with a velocity of 5 m/s and 10 m/s resp. (g =10 m/s²) Find the separation between them after one second. (5 meter)
(11) Two particles A and B are projected in the air. A is thrown horizontally and B is thrown vertically up. What is the separation between after 1 sec? ( both have speed 10 m/s) ( (12) Suppose you are riding a bike with a speed of 10 m/s due east relative to person A who is walking on the ground toward east. If your friend B walking on the ground due west measure your speed as 15 m/s due east. Find the relative velocity between two reference frames A and B . (5 m/s toward the east) (13) A swimmer capable of swimming with a velocity of 10 m/s relative to water jumps in a flowing river having a velocity of 5 m/s. The man swims a distance of 200 m downstream and returns back to the original position. Find out the time taken in complete motion. (160/3 sec) (14) A person walks up a stationary escalator in t second. He remains stationary on the escalator, then it can take him up in T second. If the length of the escalator is L. Then (a) Determine the speed of man w.r.t the escalator. (15) Let us consider a boat that moves with a velocity of 5 km/h relative to water. At time t=0, the boat passes through a piece of cork floating in water while moving downstream. If it turns back at 30 min. When and where does the boat meet the cork again? (1 hr) (16) A motorboat going down the stream overcame a floating body at point A. 1 hour later it turned back and after some time passed the floating body at a distance of 6 km from point A down the stream. Find the river flow velocity. Assume the effect of the engine to be constant. ( 3 km/h) (17) Two towns A and B are connected by a regular bus service with a bus leaving in either direction every T min. A man cycling with a speed of 20 km/h in direction A to B notice that a bus goes past him every 18 min in the direction of his motion, and every 6 min in the opposite direction. What is the period T of the bus service and with what speed (assume constant) do the buses ply on the road? (40 km/h, 9 min) (18) Two trains each of length are running at constant speeds on parallel tracks while moving in the same direction one overtakes the other in seconds and while moving in the opposite direction one crosses the other in seconds. find the speeds of both trains. (3.75 m/s, 1.25 m/s) |
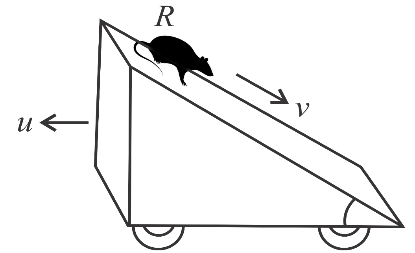
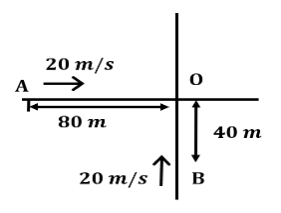
Numerical Questions for Relative Motion in 2-D(1) Particle A is moving at a speed of 30 m/s toward the east and particle B is moving at a speed of 40 m/s toward the north. Find the velocity of A relative to B and the velocity of B w.r.t A. (draw the fig) ( 30i-40j) (2) A bird is flying due east with a velocity of 4 m/s. The wind starts to blow with a velocity of 3 m/s due north. What is the magnitude of the relative velocity of a bird w.r.t wind? Find out its direction also. ( 5 m/s, 37° from east toward south) (3) A monkey is climbing a verticle tree with a velocity of 12 m/s while a dog runs towards the tree chasing the monkey with a velocity of 16 km/h. Find the magnitude of the velocity of the dog relative to the monkey. ( 20 m/s) (4) A truck is moving at a constant velocity of u=54 km/h. In what direction should a stone be projected up with a velocity of 30 m/s from the floor of the truck, so as to appear at right angles to the truck for a person standing on the ground? ( 120°) (5) A wind is blowing at a speed of 30√2 km/h in the north-east direction. If the car starts at a speed of 40 km/h towards the north. Find the direction of the flag on the car. (6) A rat is moving down the slant of a wedge of the angle of inclination θ with a velocity v as shown in the figure. If the wedge moves towards the left with velocity u. Find
(a) Velocity of that rat relative to ground. |
RIVER PROBLEM ( WHEN CROSSING)
In this section, we are going to deal with the motion of a swimmer when crossing a river which is flowing. Some terms related to river problem.
velocity of swimmer relative to river ( velocity of swimmer in still water)
velocity of the river relative to the ground ( River flow velocity)
NOTE:- velocity of floating bodies is equal to the river flow velocity.
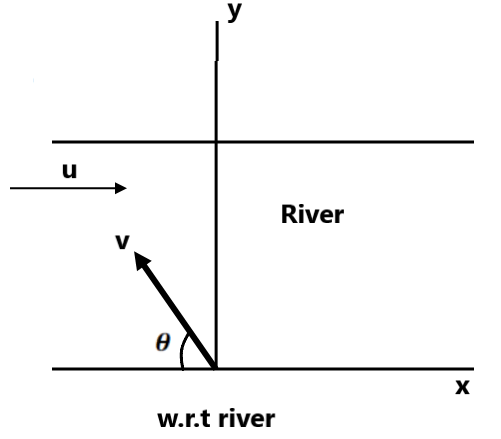
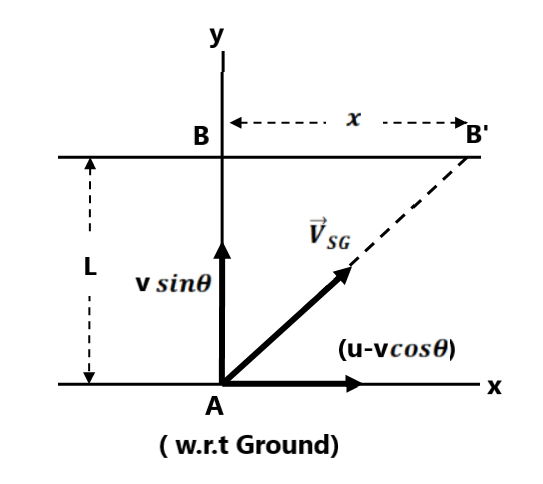
Here
(a) Time taken to cross the river,
(b) Horizontal drift
Here
can be +ve, -ve, or 0.
(c) Crossing the river along the shortest path.
For the shortest path, drift=0 i.e. velocity of swimmer w.r.t ground along x direction must be zero.
i.e.
Crossing time
Note that for the shortest path ( i.e. velocity of the swimmer relative to the river must be greater than river flow velocity)
(d) Crossing the river in the shortest possible time
Now For
to be minimum
must be maximum.
i.e.
and
In this case, horizontal drift can not be zero
(e) Minimum drift in crossing the river
For to be minimum
Solving it, we get
Putting the value of θ in equation (1) we get the minimum drift
Note that minimum drift occurs only when ( velocity of swimmer w.r.t river < river flow)
Numerical for River Problem in 2D(1) A boatman can row at a speed of 10 km/h in still water. If the river flows steadily at 5 km/h , in which direction should the boatman row in order to reach a point on the other bank directly opposite to the point from where he started? The width of the river is 2 km. ( 120° with river flow) (2) A boat that has a speed of 5 km/h in still water crosses a river of width 1 km along the shortest possible path in 15 min. Calculate the velocity of river water. (3 km/h) (3) A man can swim at a speed of 3 km/h in still water. He want to cross a 500 m wide river flowing at 2 km/h. He keeps himself always at an angle 120° with the river flow while swimming. (a) Find the time he takes to cross the river (1/3√3 hr) (4) A river 400 m wide is flowing at a rate of 2 m/s. A boat is sailing at a velocity of 10 m/s w.r.t the water in a direction perpendicular to the river. (a) Find the time taken by the boat to reach the opposite bank. ( 40 sec) (5) A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed w.r.t water is 3 km/h. (a) If he heads in a direction making an angle θ with the flow, find the time he takes to cross the river. ( 10/sinθ min) (6) A man can swim at the rate of 5 km/h in still water. A 1 km wide river flows at the rate of 3 km/h. The man wishes to swim across the river directly opposite to the starting point. (a) Along what direction must the man swim? |
Rain Problems and MiscellaneousIf the speed of man is increased along the +ve x-axis, then Rain rotates always clockwise w.r.t man
(1) A man moving with 5 m/s observes rain falling vertically at the rate of 10 m/s. Find the speed and direction of the rain w.r.t ground. ( 5√5 m/s, (2) A man standing, observes rain falling with the velocity of 20 m/s at an angle of 30° with the vertical. (a) Find out the velocity of man so that rain appears to fall vertically. (3) A man walking at a speed of 4 m/s on a horizontal road. The rain appears to him to be falling vertically. He increases his speed to 8 km/h and then the rain appears to make an angle of 30° with the vertical. Find the velocity of the rain w.r.t ground. (4) A man is walking down an incline of angle 30°. When he walks down the incline at speed 2√3 m/s he has to keep his umbrella vertical to protect from rain. If the actual speed of rain is 5 m/s. At what angle with the vertical should he hold the umbrella at rest so that he does not get drenched? (37°) (5) A bird is flying due east with a velocity of 4 m/s. The wind starts to blow with a velocity of 3 m/s due north. What is the magnitude of the relative velocity of a bird w.r.t wind? Find out its direction also. ( 5 m/s, 37° from east toward south) (6) An airplane pilot wishes to fly due west. A wind of 100 km/h is blowing towards the south. (a) If the speed of the plane w.r.t air is 300 km/h. In which direction should the pilot head? |
SPECIAL CASE:-
1. Velocity of separation and velocity of approach:-
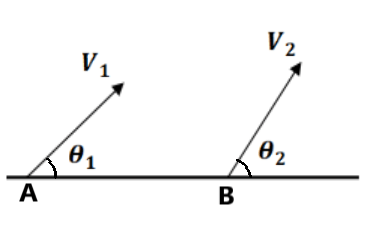
Here AB is the line joining the two particles.
If Then Velocity of Approach
If Then Velocity of Separation
i.e. instantaneous velocity of approach and separation depends only on the component velocity along the line joining them.
|
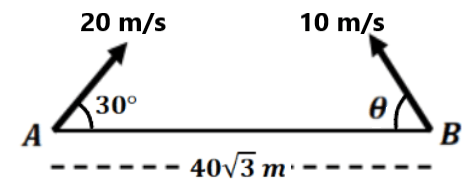
(1) Find their velocity of approach and separation before and after crossing.
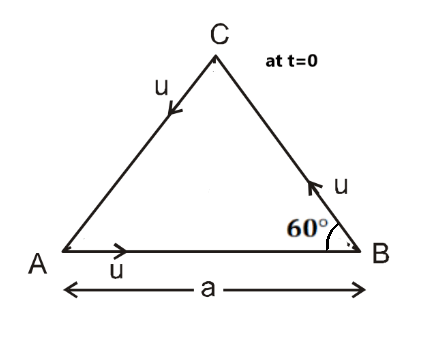
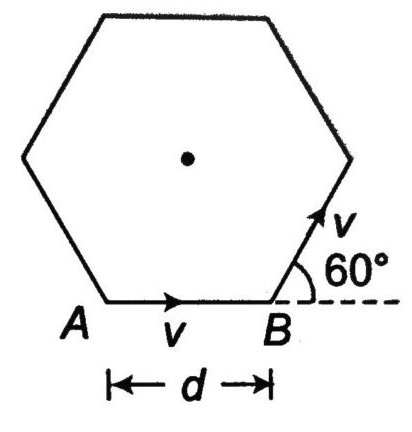
(2) A stone is dropped into the water from a bridge 44.1 m above the water. Another stone is thrown vertically downward one second later. Both strike the water simultaneously, then find the initial speed of the second stone. (12.25 m/s) (3) At what time will the all particles meet each other? At t=0 All particles are situated at the corner of the polygon. ( 2a/3u, 2d/v)
|
2. Shortest distance of approach:-
|
(1) Find the closest distance between particles A and B. (6 km, 4√5 km)
(2) A ship A steams due north at 16 km/h and ship B due west at 12 km/h. At a certain moment, the position of B is (3) Two particles A and B are moving with uniform velocities as shown in the figure given below at t=0. Find out the shortest distance between the two particles. (20√2 m)
|
3. Collision of the two bodies”-
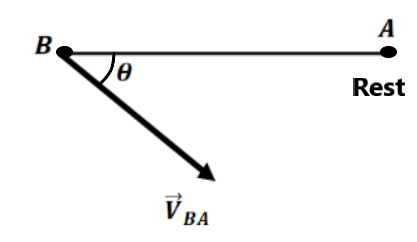
For B to collide with A, θ must be zero. i.e. Relative velocity must be along the line joining them.
Ex-
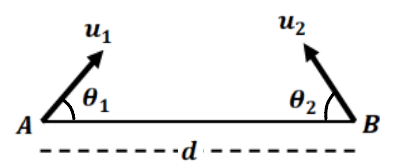
Here for collision, the velocity of A w.r.t B must be along the line joining them.
and relative velocity perpendicular to AB i.e. along Y- axis must be zero.
i.e.
The time taken to collide is
|
(1) Two cars A and B are moving with speeds of 30 m/s and 40 m/s on two different roads with are at right angles to each other. The initial separation between them is 1000m. Assuming that the cars will collide find the time after which they collide. ( 20 sec) (2) Find the value of θ for A and B to collide. Also, find the time taken to collide. ( 90°, 4 sec)
|
Questions(1) can the relative velocity of two bodies be greater than the absolute velocity of either body? (2) Even when rain is falling vertically downwards, the front screen of a moving car gets wet while the back screen remains dry. Why? (3) When an observer is standing on Earth, the trees and houses appear stationary to him. However, when he is sitting in a moving train, all these objects appear to move in a backward direction. Why? (4) Draw a position-time graph for two objects having (a) zero and (b) non-zero relative velocity. (5) When two cars A and B move towards each other with constant velocities v1 and v2, the distance between them decreases by 10 m/s. When they move in the same direction with the same speed, the distance between them increases by 5 m/s. What are their velocities? |