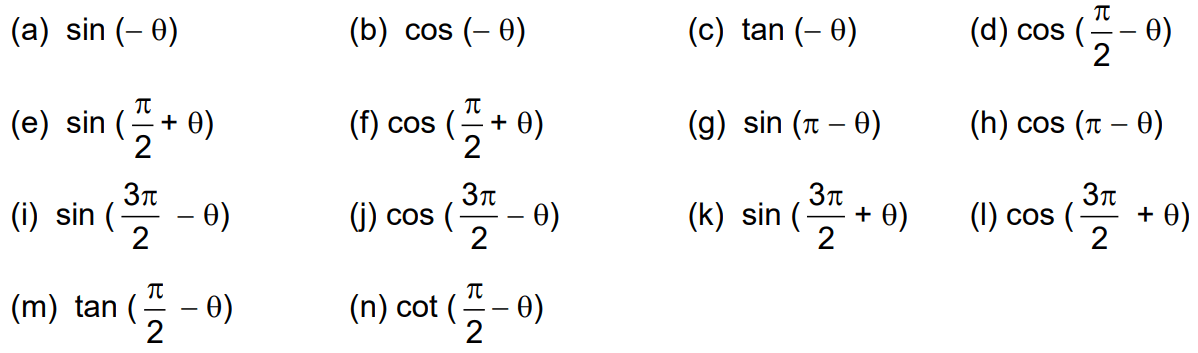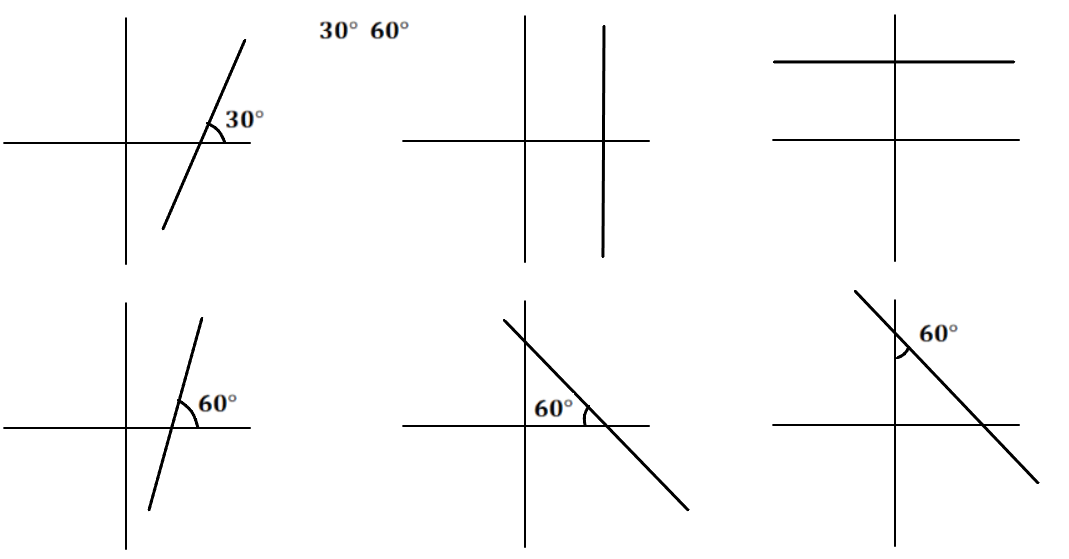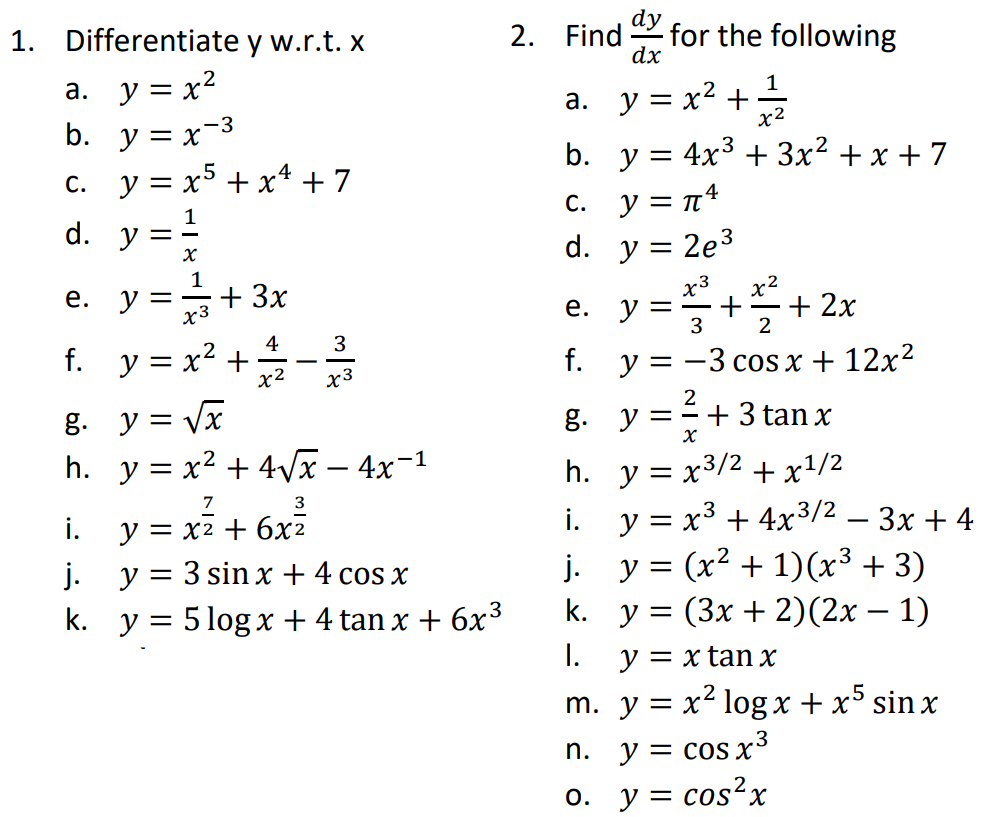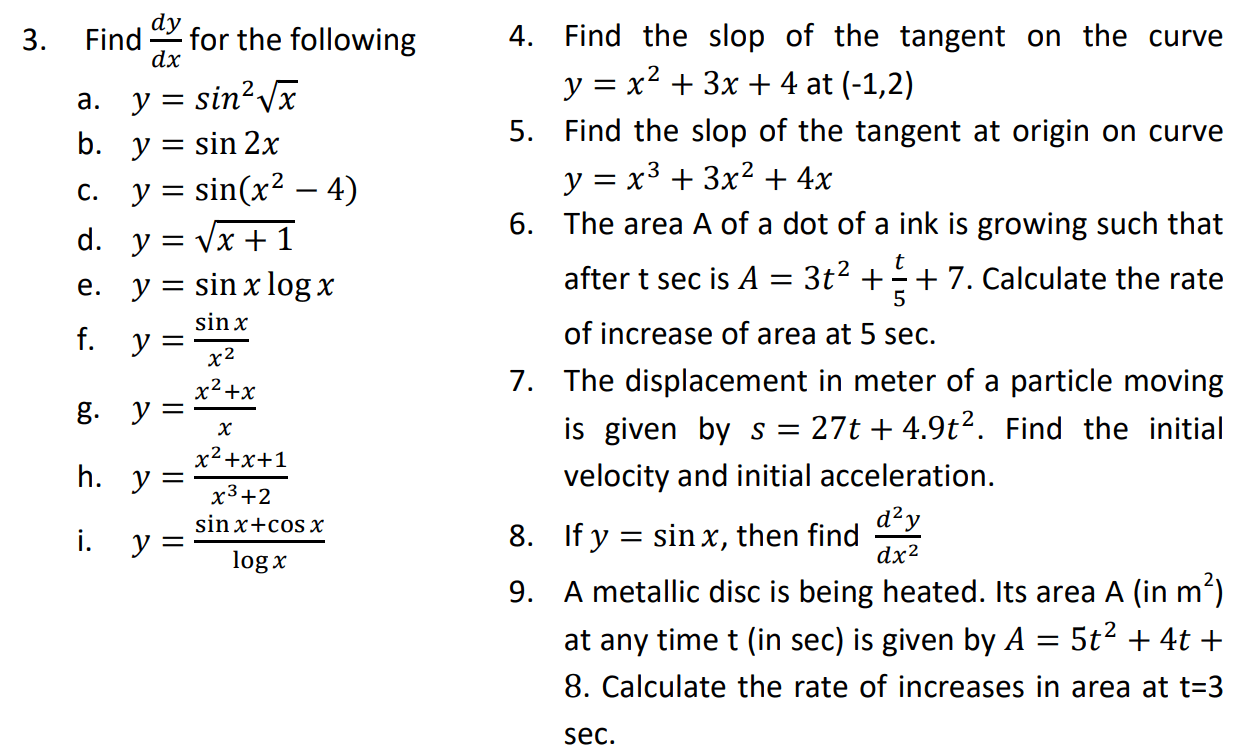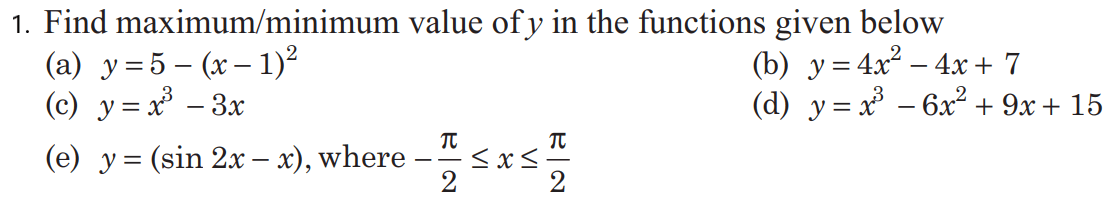MATHEMATICAL TOOLS -

Mathematics is the language of physics. It becomes easier to describe, understand, and apply the physical principles if one has a good knowledge of mathematics.

For Example, Tools are required to do physical work easily and mathematical tools are required to solve numerical problems easily

TRIGONOMETRY

[Measurement of angle and relationship between degrees and radian]

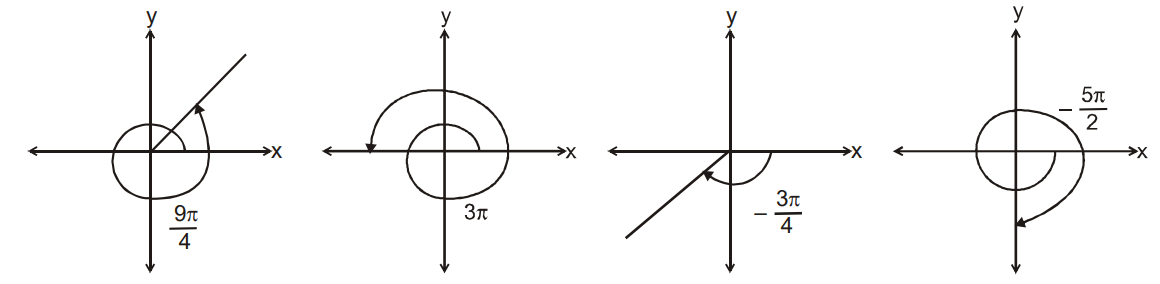
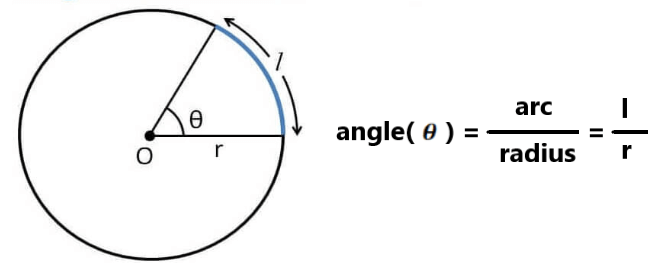
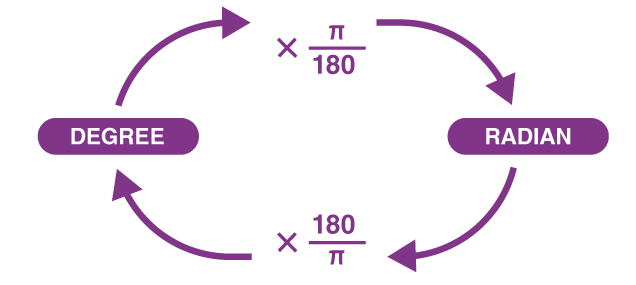
Angle is expressed in Radian or Degree.

$\dpi{120} \fn_cm \mathbf{\left [ \pi \;radian=180^{\circ} \right ]}$ In radian, value of π is 22/7 or 3.14

Q.1 Convert degree into radian

30°, 60°, 120°, 45°, 150°, 270°, 360°, 137°, 18°, 300°, 390°, 600°, 315°, 240°, 340°, 570°, 225°

Q.2 Convert radian into degree

π/3, π/2, 3π/2, 2π/3, π/6, π/4, 13π/6, 5π,3, 1.3, 3.14, 8Π/3,

In a full circle, there are 360°. Each degree is split up into 60 parts known as minutes $\fn_cm ({}')$

$\dpi{120} \fn_cm i.e.\; {1}'=\frac{1}{{60}^0}$

and each minute $\fn_cm (')$ is split up into 60 parts known as seconds $\fn_cm ('')$

$\dpi{120} \fn_cm i.e. \; 1''=\frac{1}{60'}$

Q.3 Convert 40°20’50” into degrees.

Ans. $\dpi{120} \fn_cm 40^020'50''=40+\frac{20}{60}+\frac{50}{60\times60}=40.3472^0$

Q.4 Convert $\fn_cm 40.3472^0$ into minutes and seconds.

Ans. $\dpi{120} \fn_cm 40.3472^0=40^0+(0.3472)^0=40^0+(0.3472\times60)'=40^0+(20.832)'$

$\dpi{120} \fn_cm =40^0+20'+(0.832)'+40^0+20'+(0.832\times60)''=40^0+20'+50''$

$\dpi{120} \fn_cm =40^020'50''\;\;\;\;\; ans$

Q.5 Convert

40°30′ into degrees

100′ into degrees (1.66°)

7200” into degrees (2°)

30° into minute ( 1800)

60.325° into degrees, minutes and seconds (60°19’30”)

48°28’32” into degrees (48.4756°)

52.3157° into degrees, minutes and seconds (52°19’3”)

72.4813° into degrees, minutes and seconds (72°28’53”)

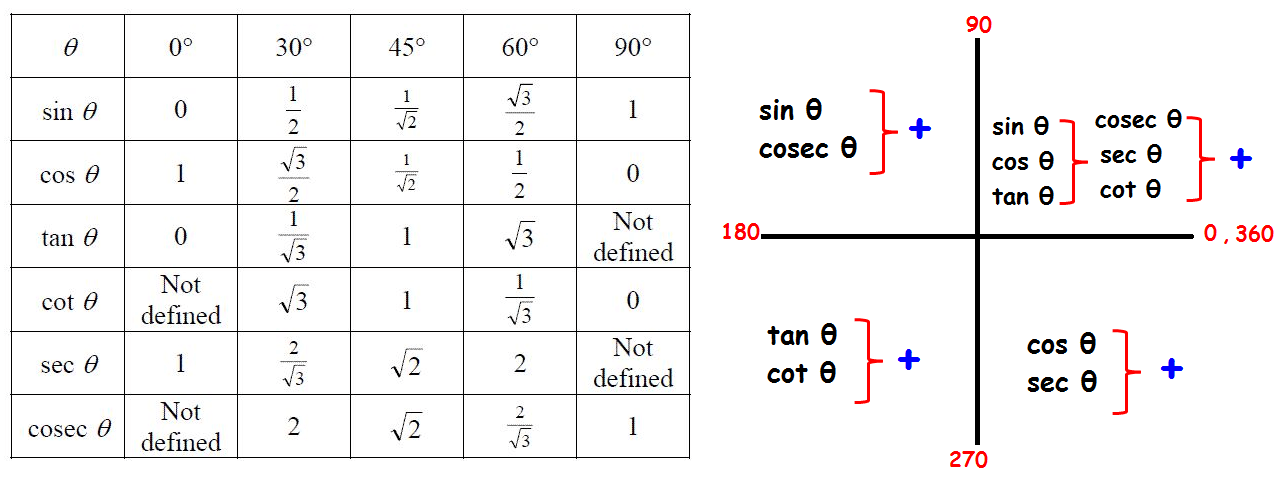
Q.6 Find the value of sin420°.

Ans: At first, write $\dpi{120} \fn_cm \sin420^0=\sin(90\times \textbf{\underline5}-30^0)$

here 5 is an odd number, so sinθ converted into cosθ. If this number is even then no conversion takes place.

$\dpi{120} \fn_cm \left ( Conversion\; is\; like\;\sin\theta\rightleftharpoons \cos\theta , \tan\theta\rightleftharpoons \cot\theta, \sec\theta\rightleftharpoons cosec\;\theta\right )$

After that, we have to check which quadrant $\dpi{120} \fn_cm (90\times5 - 30^0)$ is in. Here it lies on the 1st quadrant and sinθ is +ve in this quadrant.

so finally we can write $\dpi{120} \fn_cm \sin420^0=\sin(90\times \textbf{\underline5}-30^0)=\cos 30^0= \frac{\sqrt{3}}{2}$

Q.7 Find the value of 330°.

Ans. $\dpi{120} \fn_cm \sin330^0=\sin(90\times \textbf{\underline4}-30^0)=-\sin 30^0= -\frac{1}{2}$

Q.8 Find the value of

$\dpi{120} \fn_cm \sin405^0\;\;\;\;\;\sin300^0\;\;\;\;\;\sin37^0\cos53^0\;\;\;\;\;\tan765^0\;\;\;\;\;\tan1020^0$

$\dpi{120} \fn_cm \tan390^0\;\;\;\;\;\tan120^0\;\;\;\;\;\cot405^0\;\;\;\;\;\tan135^0\;\;\;\;\;\sin840^0$

$\dpi{120} \fn_cm \cos120^0\;\;\;\;\;\tan210^0\;\;\;\;\;\cos210^0\;\;\;\;\;\cos150^0\;\;\;\;\;\csc 120^0$

$\dpi{120} \fn_cm \sin330^0\;\;\;\;\;\tan225^0\;\;\;\;\;\tan330^0\;\;\;\;\;\sec495^0\;\;\;\;\;\cos(-30^0)\;\;\;\;\; \sin(-120^0)$

Important Formula

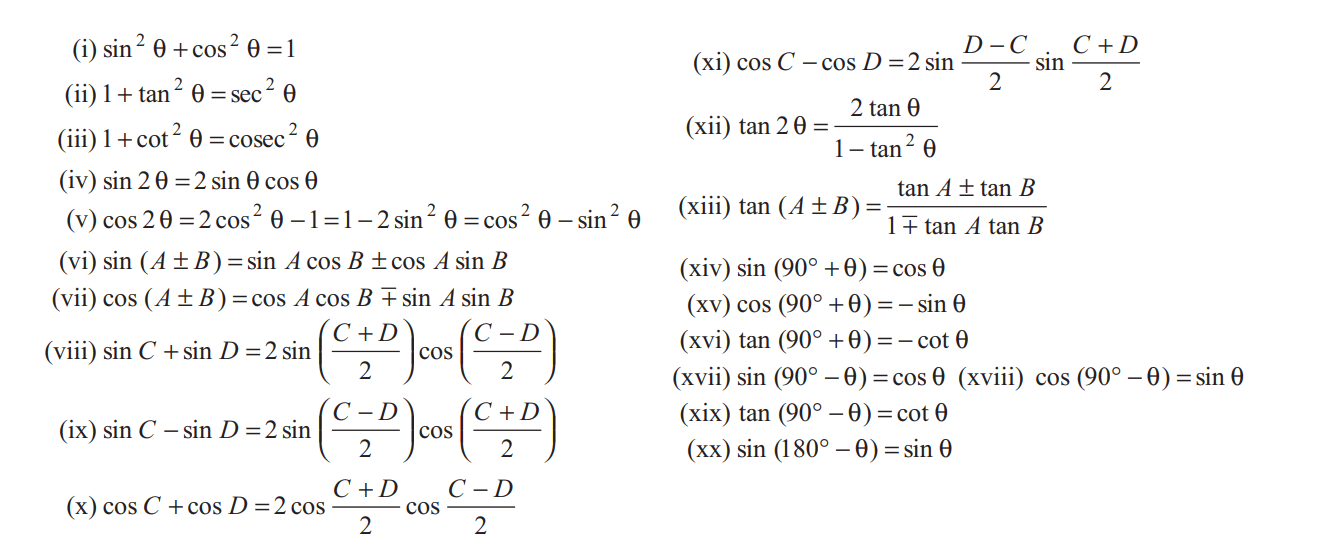
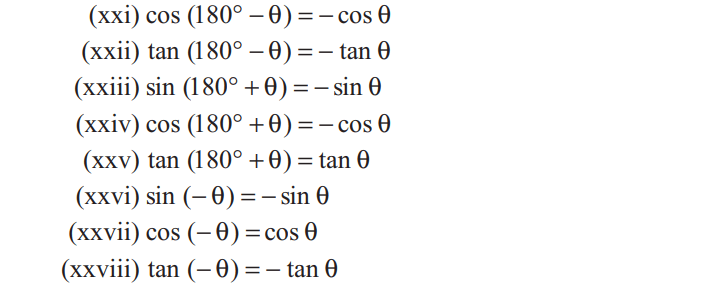
Q.9 Find the value of

Q.10 Find the value of

$\dpi{120} \fn_cm \sin15^0\;\;\;\cos15^0\;\;\;\sin75^0\;\;\;\cos75^0$

$\dpi{120} \fn_cm \sin105^0\;\;\;\cos105^0\;\;\;\cos106^0$

Hint:- sin15°=sin(45°-30°), cos106°=cos(2×53°)

Q.11 If $\dpi{120} \fn_cm \sin\theta=\frac{1}{2}$ find the value of $\dpi{120} \fn_cm \sin2\theta, \cos2\theta\;and\; \tan2\theta$ $\dpi{120} \fn_cm \left ( \frac{\sqrt3}{2}, \frac{1}{2} \right )$

Q.12 If $\dpi{120} \fn_cm \sqrt{\frac{1+\cos\theta}{1-\cos\theta}}=\frac{1}{\sqrt3}$ Then find the minimum value of $\dpi{120} \fn_cm \theta$ . $\dpi{120} \fn_cm \left ( 120^0 \right )$

Q.13 If $\dpi{120} \fn_cm \cos\theta=\frac{4}{5}$ , then find the value of other trigonometrical ratios.

Q.14 If $\dpi{120} \fn_cm \alpha+\beta=\frac{\pi}{2}\;and\; \sin\alpha=\frac{1}{2}$ , then find the value of $\dpi{120} \fn_cm \beta.$ $\dpi{120} \fn_cm \left ( \frac{\pi}{3} \right )$

Q.15 If $\dpi{120} \fn_cm \theta=60^0$ , Find the value of $\dpi{120} \fn_cm \tan2\theta$ . $\dpi{120} \fn_cm (\sqrt3)$

Q.16 Find the value of $\dpi{120} \fn_cm \tan75^0$ . $\dpi{120} \fn_cm (2+\sqrt{3})$

Q.17 Find the value of $\dpi{120} \fn_cm (\sin15^0+\sin75^0)$ $\dpi{120} \fn_cm \left ( \frac{\sqrt3}{2} \right )$

Q.18 Find the value of $\dpi{120} \fn_cm (\sin75^0-\sin15^0)\;\;and\;\;(\cos15^0+cos75^0)$

Q.19 If $\dpi{120} \fn_cm \tan\theta=\sqrt{3}$ , then Find the value of $\dpi{120} \fn_cm \tan2\theta$ . $\dpi{120} \fn_cm (-\sqrt3\;or\; \frac{1}{\sqrt3})$

Some important concept

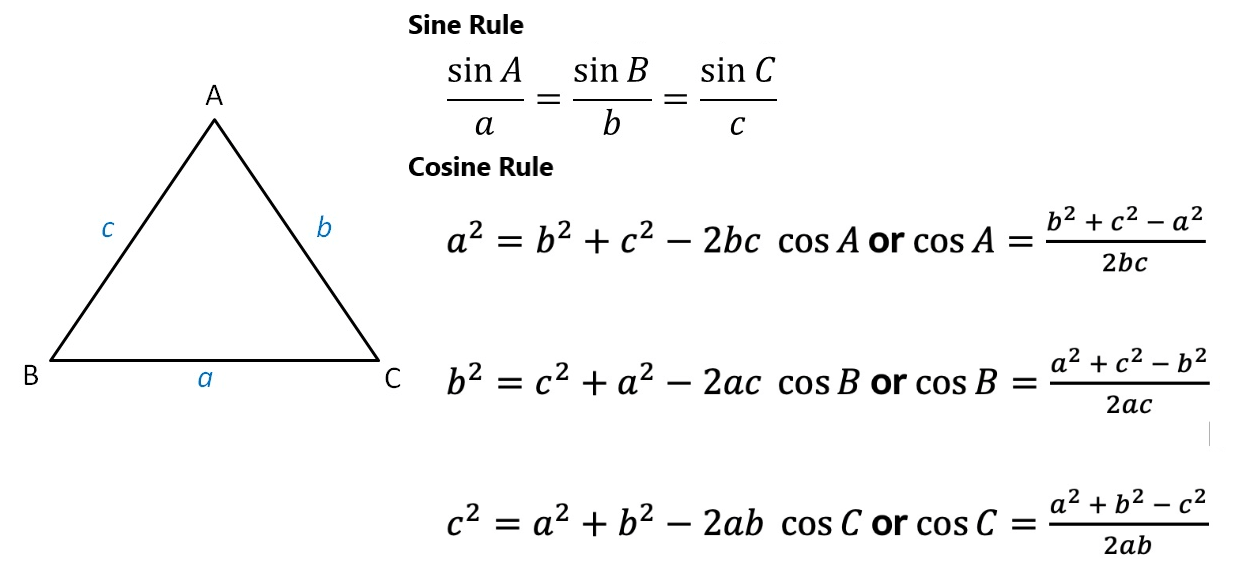
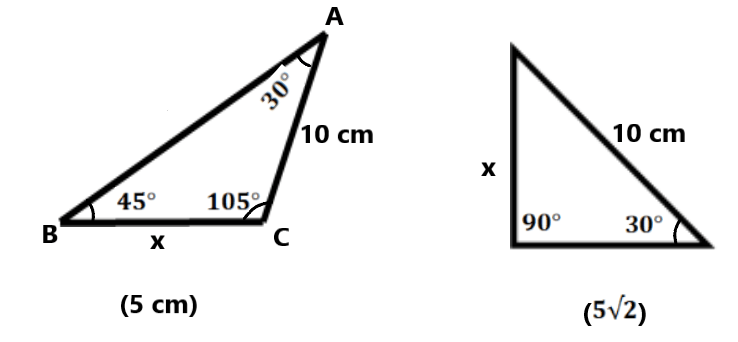
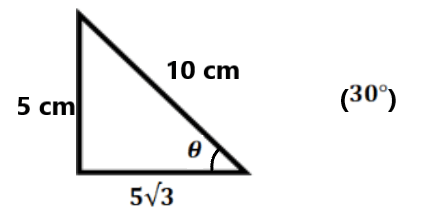
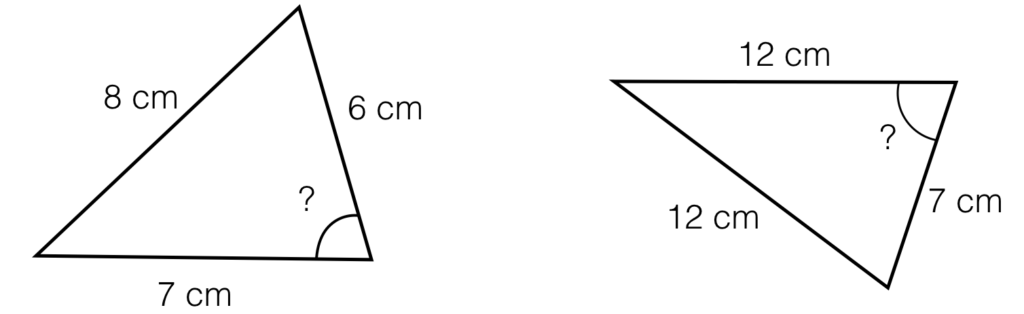
Q.20 Find x

Q.21 Find θ

CO-ORDINATE

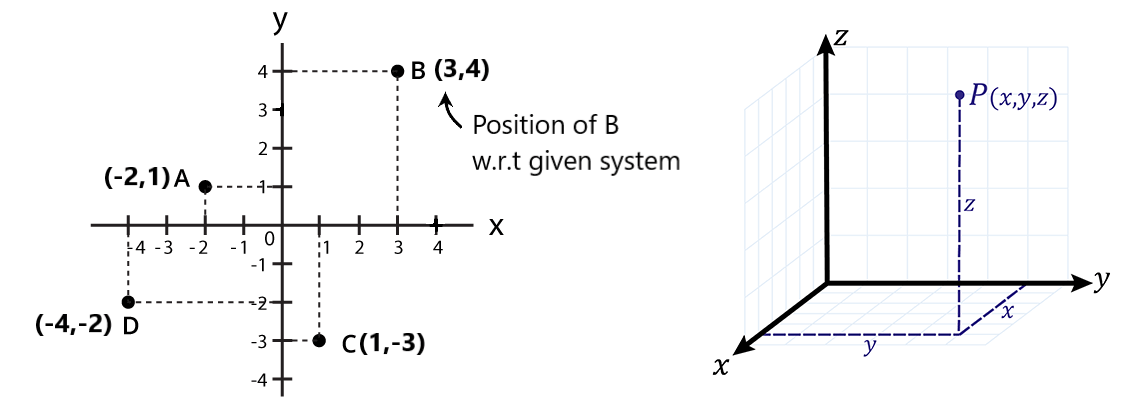
Distance Formula

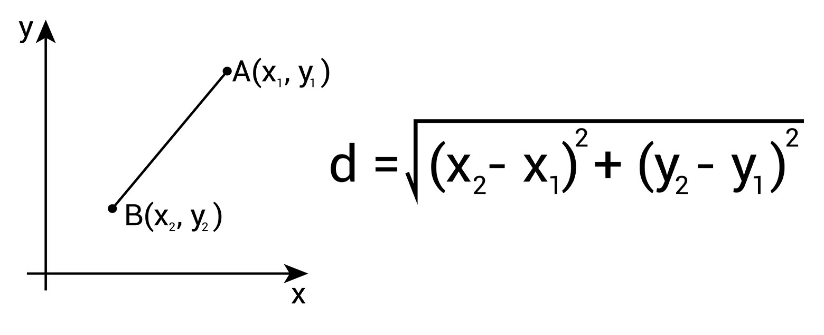
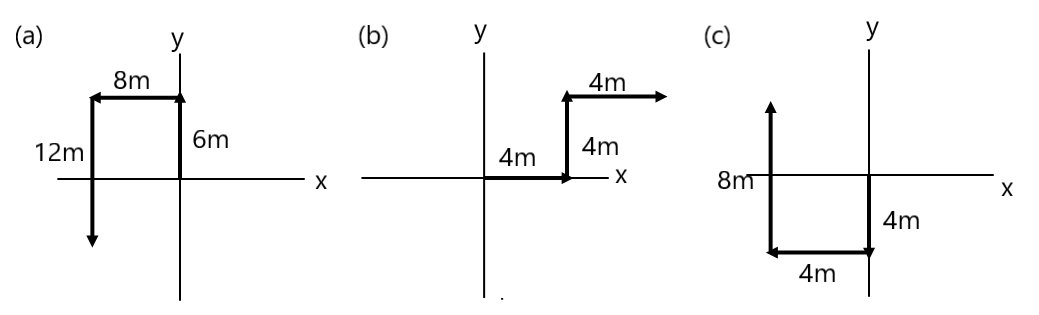
Q.1 Draw the following points in the coordinate system.

(2,2), (-5,2), (0,4), (6,3), (-3,-4), (5,0), (6,-6), (3,-2), (0,-8), (-3,0), (-3,-10)

(-8,4), (0,0), (2,3,2), (-4,-3,2), (0,4,0), (0,3,2), (-4,0,3)

Q.2 Find the distance between two given points and draw fig also.

(a) (3,2) to (2,3) (b) (0,4) to (0,-4) (c) (5,3) to (-6,-2) (d) (-3,2) to (3,-2)

(e) (0,4) to (4,0) (f) (-3,0) to (0,-8) (g) (0,0) to (3,4) (h) (-3,-4) to (3,4)

(i) (0,4,3) to (3,2,3) (j) (0,0,0) to (3,4,5) (k) (1,2,3) to (3,2,1)

Q.3 If a particle starting from its origin moves 7m along the north, it turns towards the east and moves 4m and again turns south and moves 4m. Find the final position of the particle and its displacement.

Q.4 If a particle starts from its origin, revolves a semicircular path of radius 4m on the x-y plane and reaches the x-axis. He moves 4m along the z-axis and finally, he moves 8m along the y-axis. Find the final position of the particle and its displacement.

Q.5 Find the final position of the particle and displacement from the origin.

Slope of a straight line

Slope is always for straight line

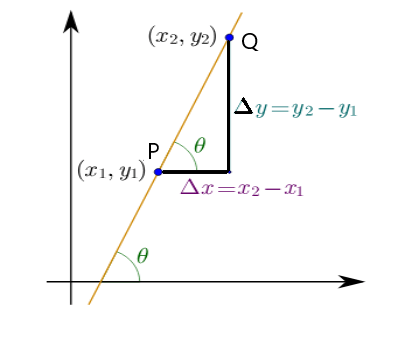
Slope (m) of a straight line PQ is tanθ where θ is the angle that the line makes with the +ve direction of the x-axis

from fig, slope of PQ is

$\dpi{120} \fn_cm m=\tan\theta=\frac{y_2-y_1}{x_2-x_1}$

$\dpi{120} \fn_cm \left [ m=\frac{\Delta y}{\Delta x} \right ]$

If PQ is very very small i.e. tends to zero ( approx point), then the slope of PQ (or say slope of approximately point) is given by

$\dpi{120} \fn_cm \left [ m=\frac{dy}{dx} \right ]\rightarrow$ differentiation of y w.r.t x.

in curve

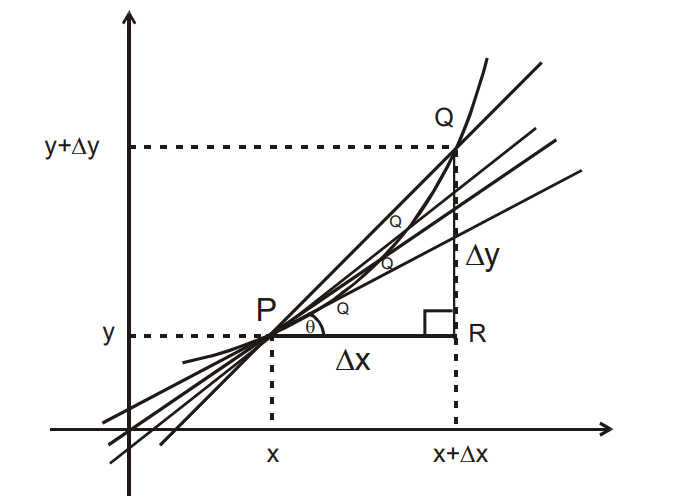
If point Q is brought closer to P gradually, then the slope of PQ is nothing but the slope of a straight line ( tangent) passing through P . That is $\dpi{120} \fn_cm \left [ m=\frac{dy}{dx} \right ]\rightarrow$ gives the slope of the tangent at a point.

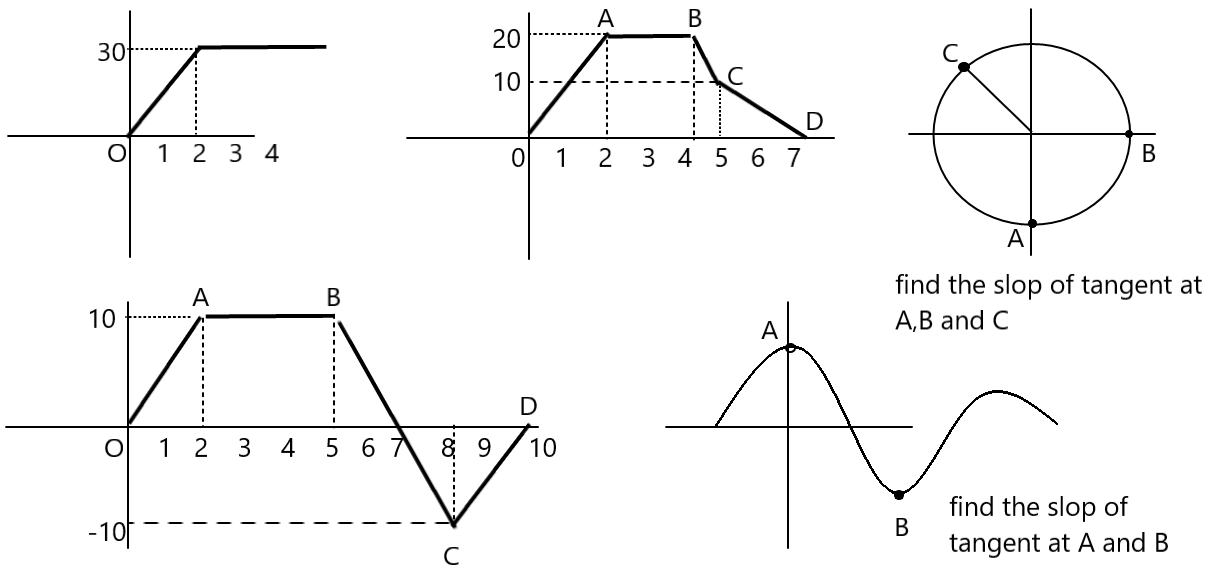
Q.6 Find the slope of the following straight line.

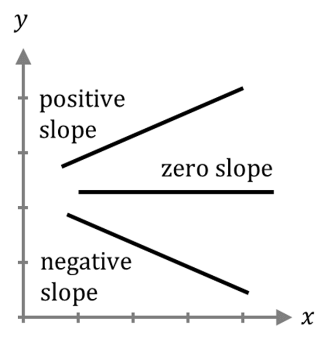NOTE:-If any line rotates anticlockwise, its slope increases. And if any straight line rotates clockwise its slope decreases.

Every curve is represented by some equation.

Straight Line

Every linear equation represents a straight line

ex- y=4x, y=4x+3, 3x-4y=6, y=3x-6 etc

♦ General equation of a straight line is Ax+By+C=0 and its slope is

$\dpi{120} \fn_cm m=\frac{co efficient\;of\;x}{coefficient\;of\;y}=-\frac{A}{B}$

♦ Equation of a straight line in slope intercept form is y=mx+c where m is the slope of straight lime and c is the intercept on the axis

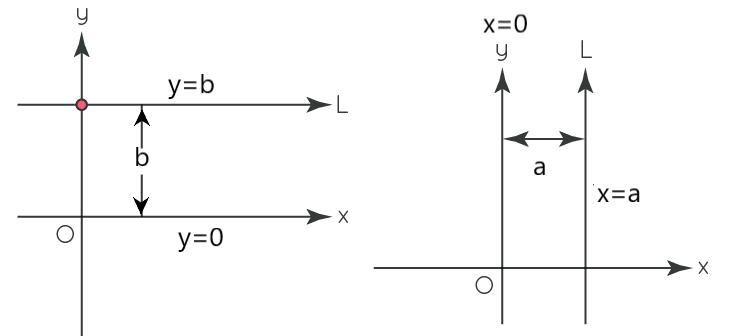
♦ The equation of x-axis is y=0 and the equation of y-axis is x=0

♦ Equation of straight line passing through (x1,y1) and (x2,y2) is

$\dpi{120} \fn_cm \left [ \frac{y-y_1}{y_2-y_1}=\frac{x-x_1}{x_2-x_1} \right ]$

Q.7 Draw straight line of the following equation and find its slope.

a. y=3x+2,
b. -3x-5y=15,
c. 2x-3y=12,
d. 3x+2y=0,
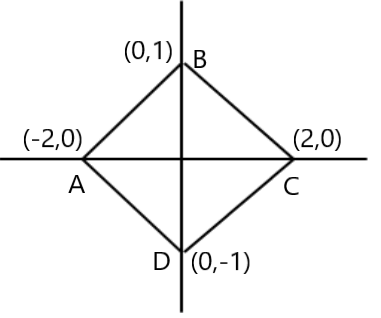
e. x-3y+6=0

Q.8 Consider two points (2,7) and (6,15). Write the straight-line equation passing through these points and find its slope.

Q.9 Consider two points (0,0) and (4,4). Write the straight-line equation passing through these points and find its slope.

Q.10 Find the equation of AB, BC, CD and DA

Parabola

Every quadratic equation represents a parabola

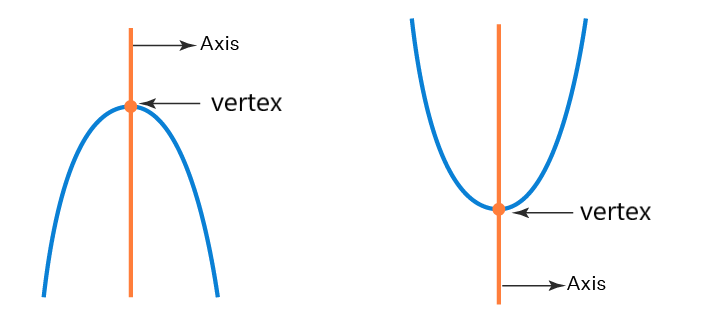
♦The general equation of a parabola is $\dpi{120} \fn_cm y=ax^2+bx+c$

Here, the x coordinate of the vertex is $\dpi{120} \fn_cm x=-\frac{b}{2a}$ and the axis of the parabola is parallel to the y-axis

if a is +ve, the graph will open up and if a is -ve, the graph will open down

♦ Simple parabola

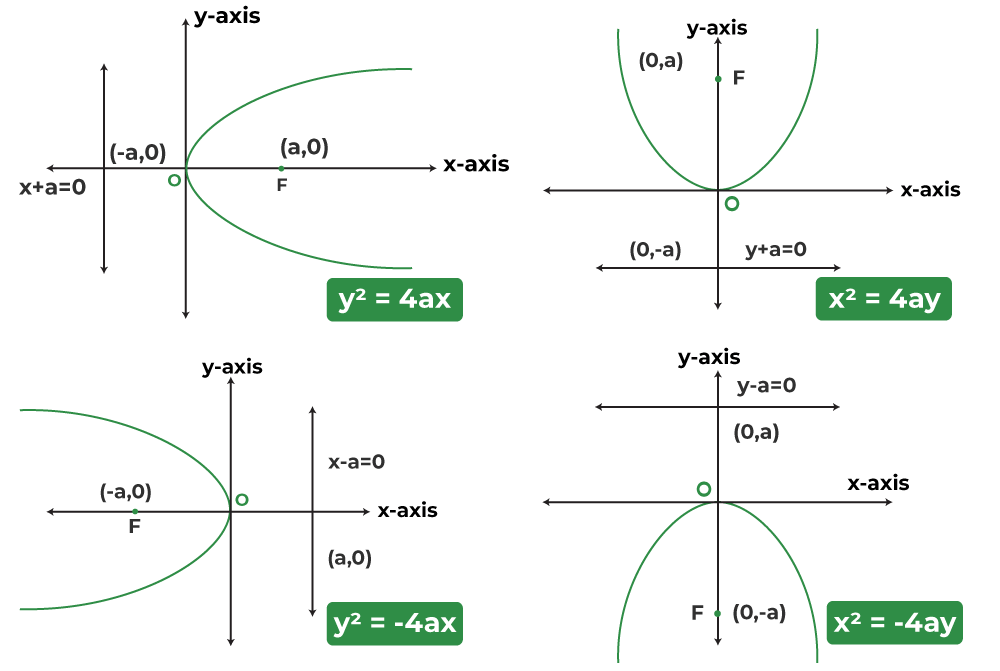
♦ $\dpi{120} \fn_cm s=ut+\frac{1}{2}at^2\rightarrow$ equation of parabola in (s-t) graph

Q.11 Draw the parabola and find its vertex

a. y²=2x
b. x²=2y+6
c. y=-x²+4x-1
d. y=-2x²+3
e. y=x²-4x
f. y=x²-8x
g. y=x²-6x+4
h. x²+2x_3=0

Other Conic Section

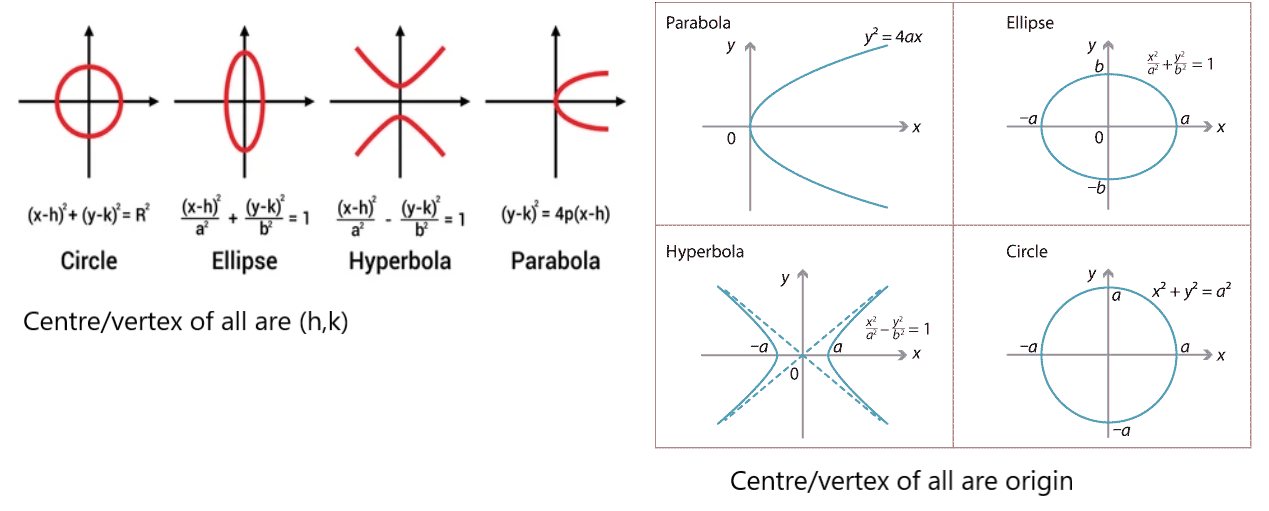
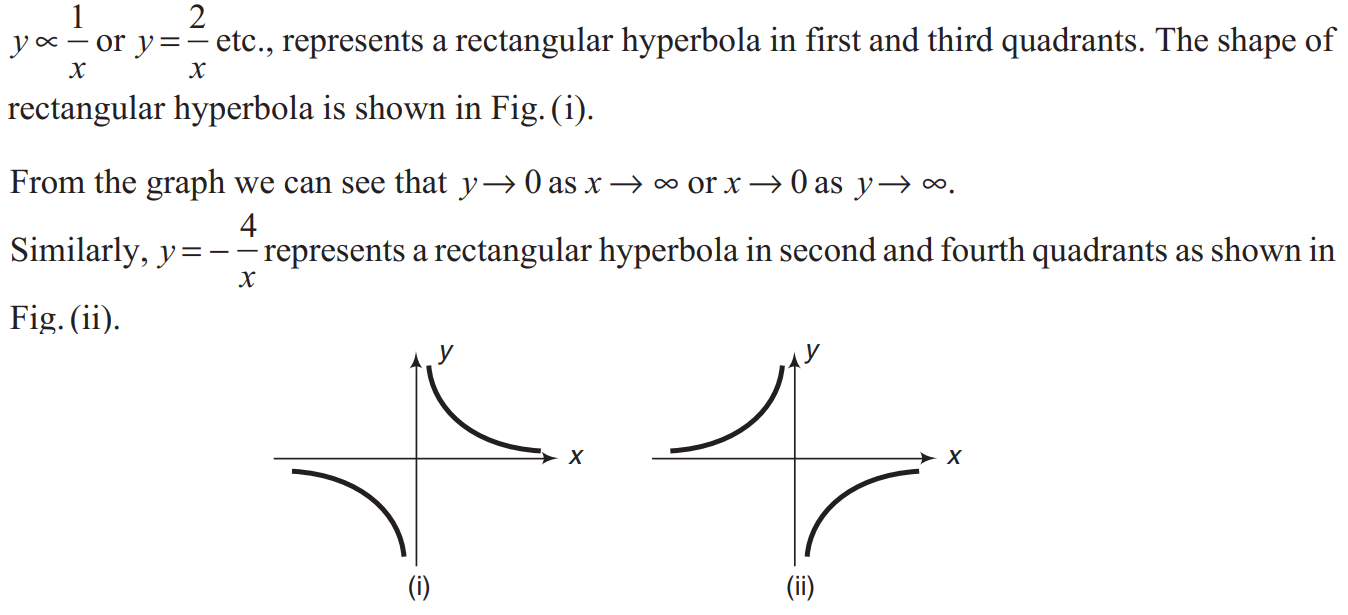
NOTE:

DIFFERENTIATION

[The purpose is to study of nature where some quantities vary ( increases or decreases)]

Constant:- whose value does not change

Variable:- Whose value changes.

For example, in relation $\dpi{120} \fn_cm y=2x+5$

2 and 5 are constant, $\dpi{120} \fn_cm x$ is variable known as independent variable, and $\dpi{120} \fn_cm y$ is a variable known as a dependent variable because their value depends upon $\dpi{120} \fn_cm x$

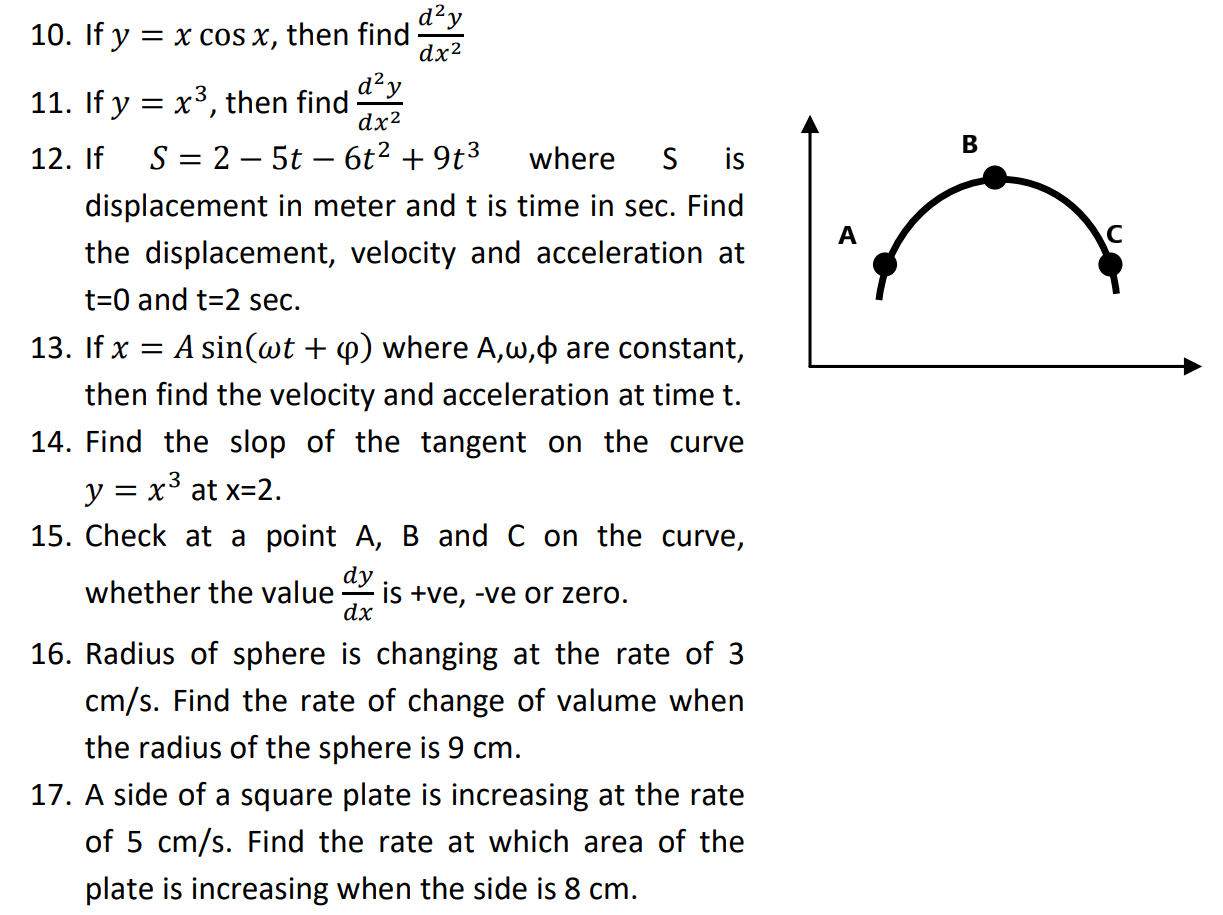
$\dpi{120} \fn_cm \frac{\mathrm{d} y}{\mathrm{d} x}\rightarrow$ differentiation of y w.r.t. x

or, Rate of change of y w.r.t. x

or a slope of tangent on the curve at a point.

Formula

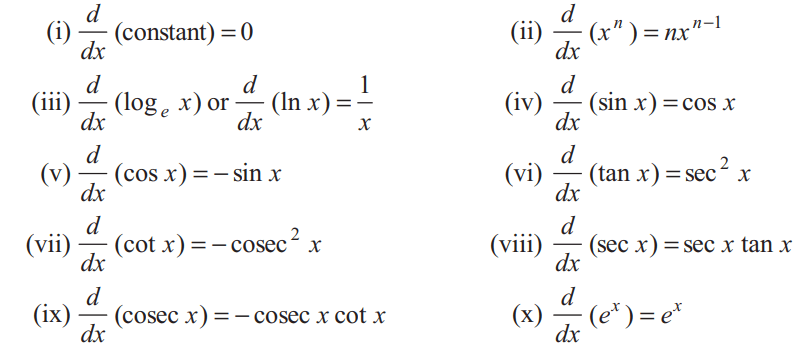
Rule

$\dpi{120} \fn_cm (i)\; \frac{d(cu)}{dx}=c\frac{du}{dx}\; where \;c\;is\;constant\;\;\;\;\;\;\;\;\;\;(ii)\;\frac{d(u\pm v)}{dx}=\frac{du}{dx}\pm \frac{dv}{dx}$

$\dpi{120} \fn_cm (iii)\; \frac{d(uv)}{dx}=u\frac{dv}{dx}+v\frac{du}{dx}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (iv)\frac{d\left ( \frac{u}{v} \right )}{dx}=\frac{v.\frac{du}{dx}-u\frac{dv}{dx}}{v^2}$

Exercise

MAXIMA & MINIMA

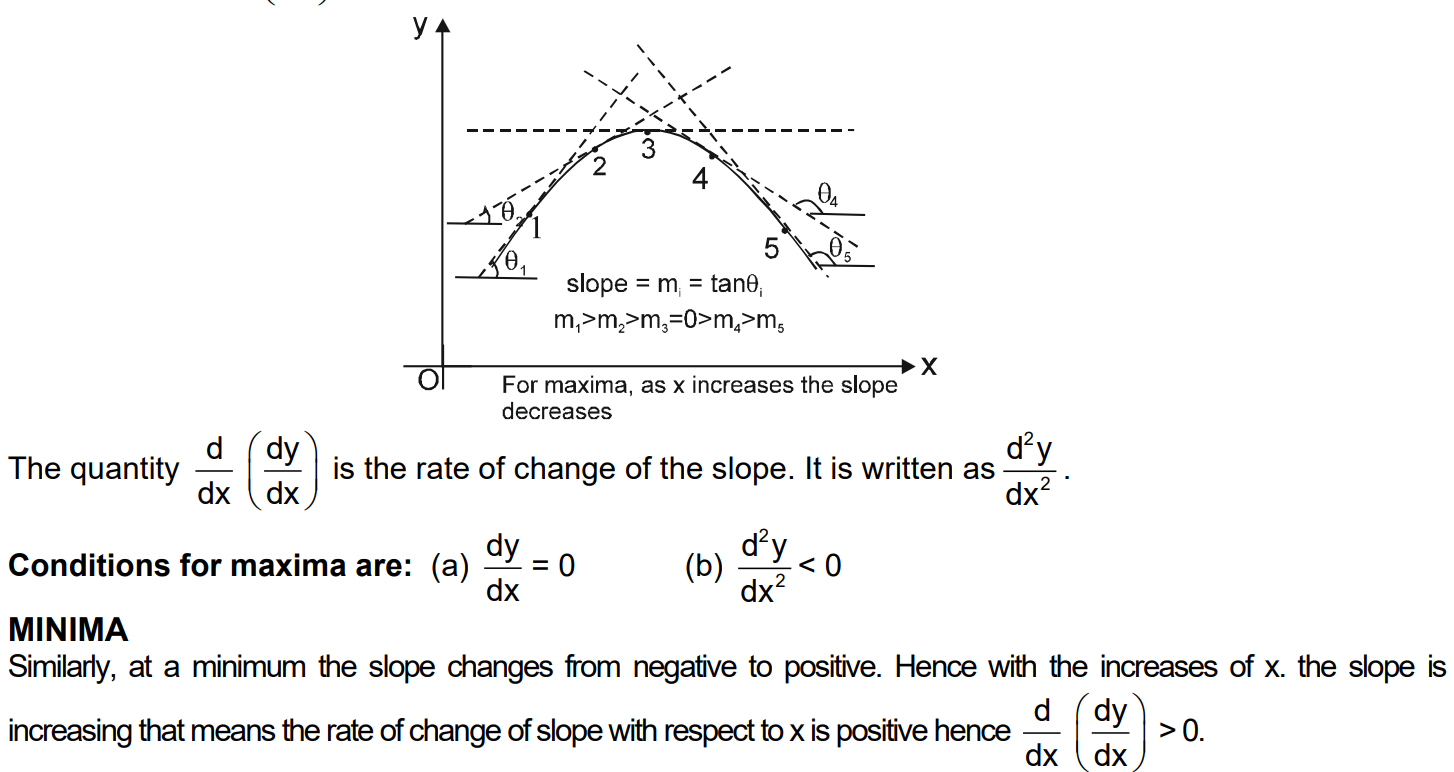
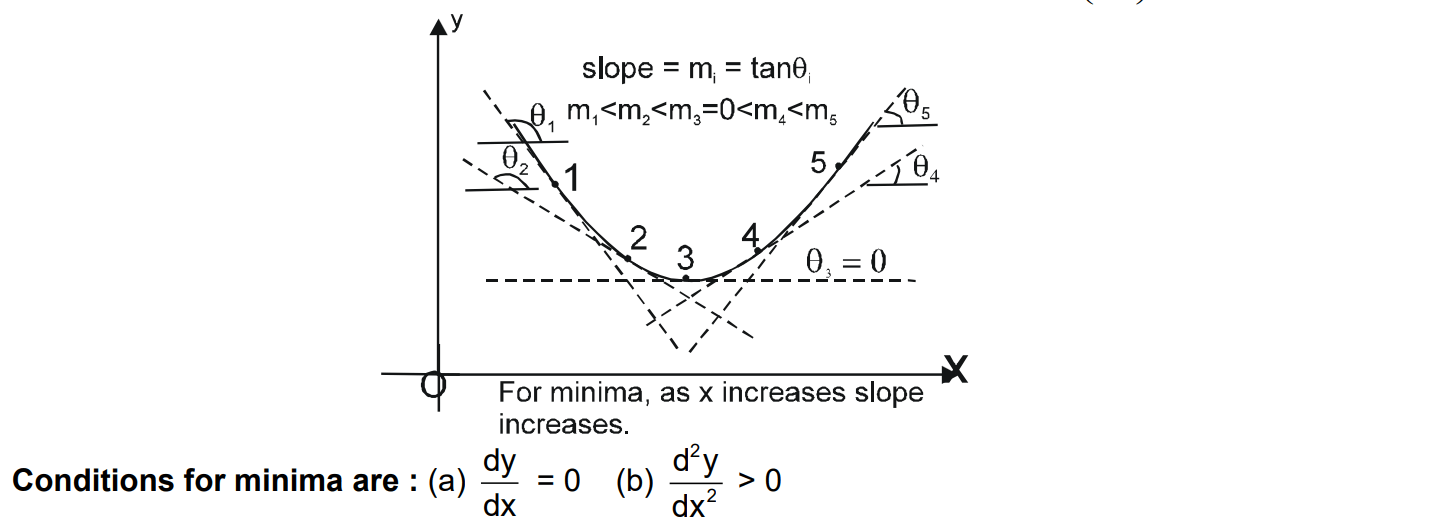
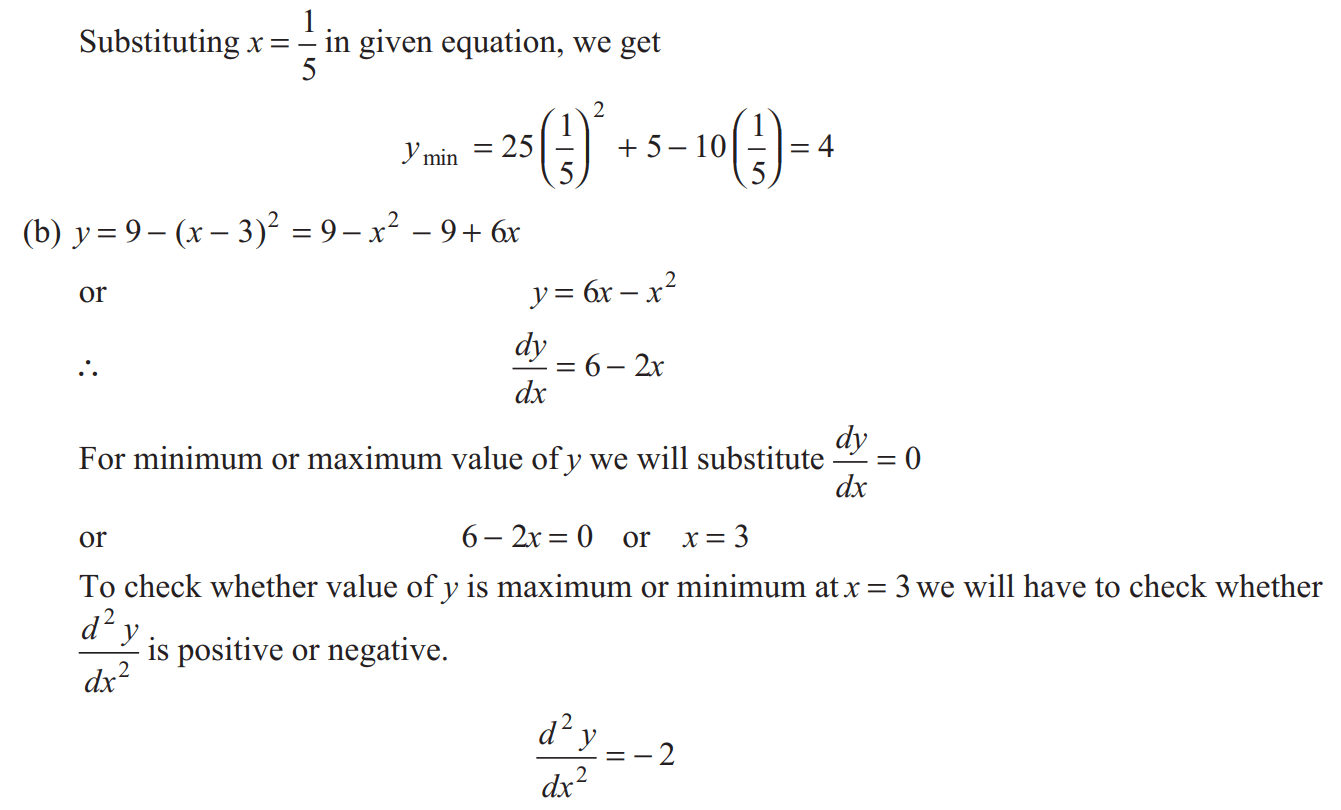
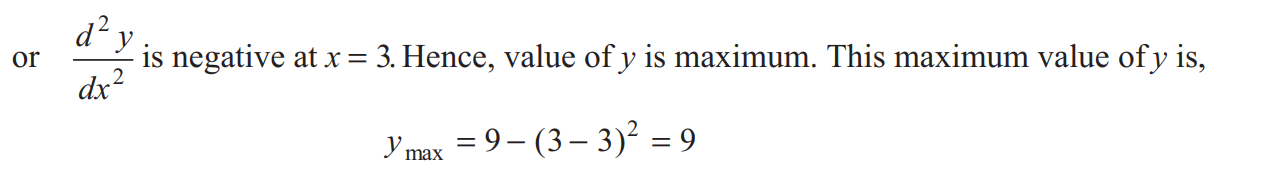
Exercise

Ans:-

Q. Find the minimum and maximum values of the function $\dpi{120} \fn_cm y=x^3-3x^2+6$ . And also find the value of $\dpi{120} \fn_cm x$ for which $\dpi{120} \fn_cm y$ is maximum and minimum. ( x=0,2/6,2)

INTEGRATION

Integration is called the inverse process of differentiation. integration is a method of adding or summing up very small parts ( tends to zero) to find the whole.

The integral calculus is of the two forms, namely

(i) Indefinite Integral:- In an indefinite integral, the range of the function is not defined, thus the value of the function obtain is followed by a constant value ‘c.’ ( denoted by $\dpi{120} \fn_cm \int$ )

(ii) Definite Integral:- Whereas in a definite integral, the range of the function is well defined, thus it gives a well-defined function. (denoted by $\dpi{120} \fn_cm \int_{a}^{b}$ )

Formula

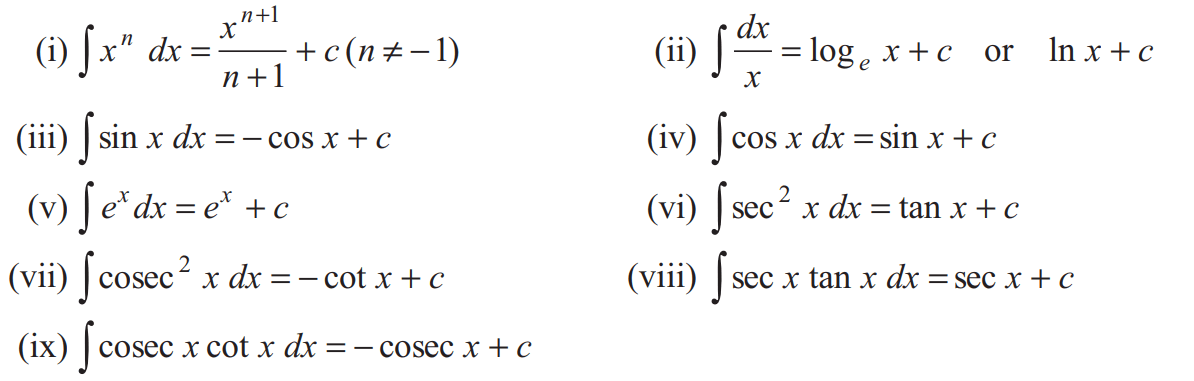
Rule

$\dpi{120} \fn_cm 1. \int c.f(x)dx=c\int f(x)dx$

$\dpi{120} \fn_cm 2. \int \left ( f(x)\pm g(x) \right )dx=\int f(x)dx + \int g(x)dx$

Rule for Definite Integration

$\dpi{120} \fn_cm I=\int_{a}^{b}f(x)dx=\left [ F(x) \right ]_a^b =F(a)-F(b)$

The integration gives an area in the graph

If $\dpi{120} \fn_cm A=\int_{x_1}^{x_2}ydx$

Here area in the (x-y) graph under the x-axis from $\dpi{120} \fn_cm x_1$ to $\dpi{120} \fn_cm x_2$ gives the value of A.

Q. Find Integration

1. $\dpi{120} \fn_cm I=\int x^3 dx$ 2. $\dpi{120} \fn_cm I=\int 5x^{-3}dx$ 3. $\dpi{120} \fn_cm I=\int (6x^2+2x)dx$ $\dpi{120} \fn_cm 4. \int (\sin x+3x^2)dx$

$\dpi{120} \fn_cm 5. I=\int (x^6-3x^{-6})dx\;\;\;\;\;6. I=\int 8x^3 dx\;\;\;\;\;7. I=\int (x^6+x^{-6})dx$

$\dpi{120} \fn_cm 8. I=\int (4x^3-3x^{-2}-2x+x-3)dx\;\;\;\;\;9. I=\int \frac{1}{x^6} dx\;\;\;\;\;10. I=\int x^{\frac{3}{2}}dx$

$\dpi{120} \fn_cm 11. I=\int \left ( x^{\frac{3}{2}}dx+x^{\frac{1}{2}}dx+5 \right )dx\;\;\;\;\; 12. I=\int (3x^{-7}-x^{-1}dx)$

$\dpi{120} \fn_cm 13. I=\int \frac{1}{x^2}dx\;\;\;\;\;14. I=\int (8+x)dx\;\;\;\;\;15 I=\int \sqrt{x}dx$

$\dpi{120} \fn_cm 16. I=\int \left ( x^4+\frac{1}{x}-1 \right )dx\;\;\;\;\;17. I=\int \left ( e^x-\frac{1}{x}-sec^2x \right )dx$ $\dpi{120} \fn_cm 18. I=\int(4x^2+3x+4)dx$

$\dpi{120} \fn_cm 19. I=\int (\sin x+\cos x)dx$ $\dpi{120} \fn_cm 20. I=\int x^{-7}dx$ $\dpi{120} \fn_cm 21. I=\int \left ( x+\frac{1}{x} \right )dx$ $\dpi{120} \fn_cm 22. I=\int 2x^{-2}dx$

$\dpi{120} \fn_cm 23. I=\int \left ( \sqrt{x}- \frac{1}{\sqrt{x}} \right )dx$ $\dpi{120} \fn_cm 24. I=\int tan^2x dx$ $\dpi{120} \fn_cm 25. I=\int (4x^3-3)dx$

$\dpi{120} \fn_cm 26. I=\int (sin x+x^{-2})dx$ $\dpi{120} \fn_cm 27. I=\int cos^2 x dx$ $\dpi{120} \fn_cm 28. I=\int \left ( x^{\frac{2}{3}}-x^{\frac{1}{2}}+5x \right )dx$

$\dpi{120} \fn_cm 29. I=\int \left ( e^{2x}+5 \right )dx$ $\dpi{120} \fn_cm 30. I=\int \sin(3x+4)dx$

Q. Find integration

$\dpi{120} \fn_cm 1. I=\int_{3}^{5}x^2dx\;\;\;\;\;\;\;\;\;\; 2.I=\int_{1}^{2}(4t+3t^2)dt\;\;\;\;\;\;\;\;\;\; 3. I=\int_{0}^{9}\frac{1}{\sqrt x}dx$

$\dpi{120} \fn_cm 4. I=\int_{0}^{\pi/4}\sin xdx\;\;\;\;\;\;\;\;\;\; 5.I=\int_{-\pi/2}^{\pi/2}\cos x dx\;\;\;\;\;\;\;\;\;\; 6. I=\int_{u}^{v}mvdv$

$\dpi{120} \fn_cm 7. I=\int_{0}^{9}x^{-1/2}dx\;\;\;\;\;\;\;\;\;\; 8.I=\int_{2}^{3}3t^2dt\;\;\;\;\;\;\;\;\;\; 9. I=\int_{1}^{2}(2+3t^2)dt$

$\dpi{120} \fn_cm 10. I=\int_{2}^{16}\frac{1}{x}dx\;\;\;\;\;\;\;\;\;\;11.I=\int_{r_1}^{r_2}\frac{Q_1Q_2}{r^2}dr\;\;\;\;\;\;\;\;\;\; 12. I=\int_{0}^{\pi/2}\sin \theta d\theta$

$\dpi{120} \fn_cm 13. I=\int_{\infty}^{R}\frac{GmM}{x^2}dx\;\;\;\;\;\;\;\;\;\; 14.I=\int_{3}^{6}(u+3t)dt\;\;\;\;\;\;\;\;\;\; 15. I=\int_{2}^{16}\frac{1}{x^2}dx$

$\dpi{120} \fn_cm 16. I=\int_{0}^{\pi}\sin^2xdx\;\;\;\;\;\;\;\;\;\; 17.I=\int_{0}^{\pi/4}\cos 2xdx$

Q. Find the area under the curve $\dpi{120} \fn_cm y=4x$ from $\dpi{120} \fn_cm x_1=0\;to\; x_2=2$

Q. Find the area under the curve $\dpi{120} \fn_cm y=3x^2$ from $\dpi{120} \fn_cm x_1=0\;to\; x_2=2$