Electric Potentital Energy -

Electric Potential Energy

Simply P.E. of a system is the energy possessed due to its configuration or position.

When a charged particle moves in an electric field, the field exerts a force that can do work on the particle. Since electrostatic forces are conservative in nature i.e. this work can always be expressed in terms of electric potential energy.

We know that the work done by force can always be expressed in terms of a P.E. as

$\fn_cm \Delta U=W_{i\rightarrow f}$ by external force or

$\fn_cm \Delta U=-W_{i\rightarrow f}$ by internal electric force

NOTE:-

(1) External force at every point of the path is to be equal and opposite to the electric force on the test charge at that point.

(2) Potential energy is always expressed in a change in P.E. i.e. $\fn_cm \Delta U=U_f-U_i$

(3) If the initial position is not specified, then choose initial position is at infinity. Because at infinity, electric P.E. is zero( Here no force exists)

i.e. $\fn_cm \left [ U_p=U_p-U_{\infty} \right ]$

” The electric potential energy of a system of point charges is the work done needed to bring the charges from an infinite separation to their final position.”

Electric potential energy of a system of two-point charges due to the mutual interaction

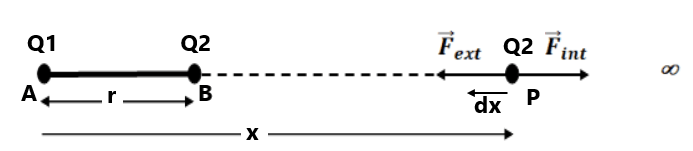
Consider two point charges Q1 and Q2 placed at points A and B which are separated by distance r. From the definition, P.E. is the work done, when point charge Q2 is taken from ∞ to point B by any path. By simplicity, we take a straight path.

Let a point P between ∞ and B which is distance x from point A on line joining AB. The electric force on Q2 at P due to Q1 is

$\fn_cm \vec{F}_{int}=\frac{kQ_1Q_2}{x^2}$ along A to B

∴ $\fn_cm \vec{F}_{ext}=\frac{kQ_1Q_2}{x^2}$ along B to A

∴ work done by this force due to small displacement dx is

$\fn_cm dw=\vec{F}_{ext}.d\vec{x}=-F_{ext}dx\cos0^0$

( here -ve sign is taken because $\fn_cm \vec{x}$ and $\fn_cm d\vec{x}$ are opposite to each other.

∴ Total work done by an external force when charge Q2 is taken from ∞ to B is

$\fn_cm w=-kQ_1 Q_2 \int_{\infty}^{r}\frac{1}{x^2}dx$

$\fn_cm =-kQ_1 Q_2 \left [ -\frac{1}{x} \right ]_{\infty}^{r}$

$\fn_cm =-kQ_1 Q_2 \left [ -\frac{1}{r}+ \frac{1}{\infty} \right ]$

$\fn_cm \left \langle w=\frac{kQ_1Q_2}{r} \right \rangle$

This work done is stored in the form of P.E of the system

$\fn_cm i.e.\;\;\;\;\mathbf{\left \langle U=\frac{kQ_1Q_2}{r} \right \rangle}$

NOTE:-

(1) P.E. is a scalar quantity, so a sign of charges must be taken. Its S.I unit is joule.

(2) P.E. of a system of charges is independent of the order of assembling of charges.

(3) P.E. of a system of point charges = Sum of P.E. of all pairs of charges in the system.

Ex- 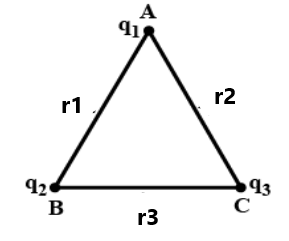$\fn_cm U=\frac{kq_1 q_2}{r_1}+\frac{kq_1 q_3}{r_2}+\frac{kq_2 q_3}{r_3}$

(4) For n charges in the system, the number of pairs = n(n-1)/2.

(5) +ve potential energy implied that work can be obtained by releasing the charges. While -ve P.E. indicates that an external agent will have to do work to separate the charge an infinite distance apart.

(6) For an attractive system U is always -ve, For a repulsive system U is always +ve, For a stable system U is minimum.

i.e. $\fn_cm U=-\frac{dU}{dx}=0$ ( for a stable system)