CIRCULAR MOTION -

When an object moves in a circular path, it is said to have circular motion.

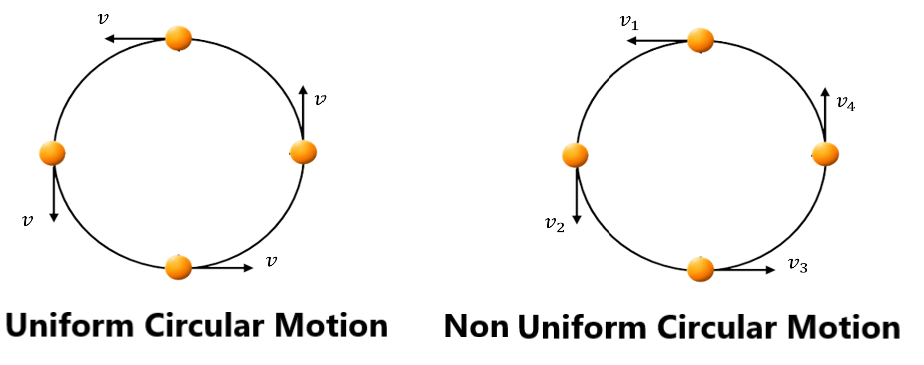
Uniform Circular Motion

Speed is constant but velocity is changed due to changes only in its direction, not magnitude. Acceleration is produced due to a change in its velocity ( direction only) known as centripetal acceleration

Non Uniform Circular Motion

Velocity changes due to changes its magnitude and direction. Acceleration is produced due to a change in velocity ( magnitude + direction). Tangential acceleration is due to a change in magnitude and centripetal acceleration is due to a change in its direction.

Important Term Related to Circular Motion

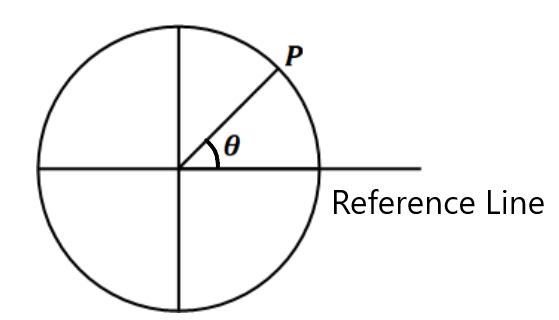
a. Angular Position(θ):- The angle made by the radius vector with a given line ( Reference Line) is called angular position. It is denoted by θ and measured in radians. ( π radian= 180°)

b. Angular Displacement(Δθ):- It is defined as the angle swept out by its radius vector in the given time interval.

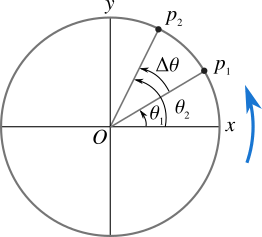
From fig angular displacement = $\dpi{120} \fn_cm \Delta\theta=\theta_2-\theta_1$

We know that $\dpi{120} \fn_cm angle=\frac{arc}{radius}$

i.e. $\dpi{120} \fn_cm \left [ \Delta\theta=\frac{\Delta s}{r} \right ]$

It is a dimensionless quantity and its S.I unit is radian (Rad)

NOTE:-

1 revolution=360°=2π radian
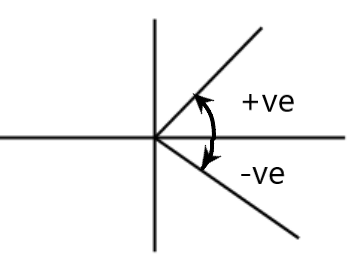
If we calculate angular displacement Δθ in an anticlockwise sense, we consider it +ve and vice versa.
In 3D finite angular displacement is a scalar quantity because it does follow the commutative law of vector addition but very small angular displacement is a vector quantity (axial vector)
But when the particle moves in a plane, the finite angle may also be treated as a vector.
Its direction is decided by the right-hand thumb rule.

Exercise 1

1. convert 30°,60°,45°,90°,120°,240° in radian.

2. What is the angle covered by the minute hand in a watch in 5 minutes in radian? Also, find the angle by second and hour hand in that time.

3. If a particle moves in a circle of radius 14 cm. Find the angle covered by the particle when it moves 11 cm in its circumference in radians. (45°)

4. Kiran goes around a circular track that has a diameter of 7 m. If she runs around the entire track for a distance of 50 m, what is her angular displacement? (14.28 rad)

5. A boy runs about 175 meters around a circular track. 35 meters is the radius of the track. What will be the angular displacement?

c. Angular Velocity(ω):- It is the rate of change of angular displacement. It is denoted by ω.

i.e. $\dpi{120} \fn_cm \left [ \omega=\frac{\Delta \theta}{\Delta t} \right ]\Rightarrow \left [ \omega=\frac{\theta_2 - \theta_1}{t_2 -t_1} \right ]$ ( Average angular velocity)

For instantaneous $\dpi{120} \fn_cm \left [ \omega=\frac{d\theta}{dt} \right ]$

It is a vector quantity ( axial vector) and its direction is the same as angular displacement. Its S.I. unit is rad/sec.

d. Time Period(T):- The time taken by a particle to complete one revolution along a circular path is called time period. It is denoted by T.

We can write $\dpi{120} \fn_cm \left [ \omega=\frac{2\pi}{T} \right ]$

e. Frequency(ν or f):- It is defined as the number of revolutions completed per unit of time. It is denoted by f or ν.

angular frequency is defined as $\dpi{120} \fn_cm f=\frac{1}{T}$

we can write also

$\dpi{120} \fn_cm \left [ \omega=2\pi f \right ]$ ( Angular frequency)

Relation between linear velocity and angular velocity

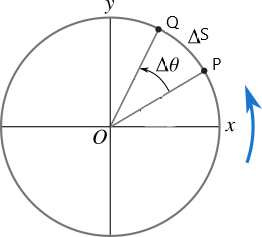
Let the particle travel from P to Q in $\fn_cm \Delta t$ time and at that time let the distance of the particle is $\fn_cm \Delta s$ .

We know that angular displacement is given by

$\fn_cm \Delta \theta=\frac{\Delta s}{r}$

divide $\fn_cm \Delta t$ both sides we get

$\fn_cm \frac{\Delta \theta}{\Delta t}=\frac{1}{r}\frac{\Delta s}{\Delta t}$

Take limits on both sides we get

$\fn_cm \lim_{\Delta t\rightarrow 0}\left ( \frac{\Delta \theta}{\Delta t} \right )=\frac{1}{r}\lim_{\Delta t\rightarrow 0}\left ( \frac{\Delta s}{\Delta t} \right )$

$\dpi{120} \fn_cm \frac{d \theta}{d t}=\frac{1}{r}.\frac{ds}{dt}$

$\dpi{120} \fn_cm \omega=\frac{v}{r}$

$\dpi{120} \fn_cm \large \therefore \;\left [ v=r\omega \right ]$

Its direction is along tangent at any point ( perpendicular to the radius vector)

NOTE:-

In vector notation $\dpi{120} \fn_cm \large \vec{v}=\vec{\omega}\times \vec{r}$
If a body makes n rotation in t seconds, then we can write $\dpi{120} \fn_cm \large \left [ \omega=\frac{2\pi n}{t} \right ]$

Exercise

1. Calculate the angular speed of a flywheel making 120 rpm. If the radius of flywheel is 7 cm. Then find the linear velocity of the tip of the flywhhel. ( 4π rad/sec, 0.88 m/s)

2. The earth makes one revolution in 24 hrs. Calculate

a. Angular speed of earth
b. The tangential speed of an object at the equator is due to the rotation of the earth.

3. A particle moves in a circle of radius 20 cm with a linear speed of 10 m/s. Find the angular velocity. (50 rad/sec)

4. Find the angular velocity of the minute and hour’s hand in a watch. (π/1800 rad/s, π/21600 rad/s)

4. If the length of the second hand of a watch is 4 cm. Then find the angular speed and linear speed if tip if second hand.( π/30 rad/s, 2π/15 rad/s)

4. If angular displacement of a particle is given by $\fn_cm \theta=a-bt+ct^2$ . Then find its angular velocity. ( -b+2ct)

5. An insect moving in a circle travels N1 revolution in an anticlockwise sense for a time T1 and N2 revolution in a clockwise sense for a time T2. Find the averaged angular speed over the time T1+T2. ( $\fn_cm \omega_{avg}=\frac{2\pi}{T_1 +T_2}\left ( \left | N_1 -N_2 \right | \right )$ )

6. A particle moves from point 1 to 2 during a time 1/2 sec. Find the average speed of the particle over 1/2 sec. ( π rad/s, 3π rad/s)

a. In anticlockwise sense

b. In clockwise sense

7. Find the average angular velocity of the particle. Time taken to one rotation is 2 sec.(0)

8. A particle is moving with constant speed in a circle as shown in fig. Find the angular velocity of the particle A w.r.t fixed point B and C if angular velocity w.r.t o is ω. (ω/2,ω/3)

9. Find the angular velocity of the particle A w.r.t B if the angular velocity of particle A w.r.t. o is ω. (ω)

10. Find the angular velocity of A w.r.t. o at the instant shown in fig. (v/2d)