Electric Potential
We know that electric field intensity is the force per unit test charge, similarly electric potential is defined as the potential energy per unit test charge.
i.e. potential at a point is defined as
Hence ” Electric potential at a point in an electric field is the amount of work done in moving a unit +ve charge slowly from infinity to that point against electric force.”
Electric Potential is a scalar quantity and its S.I unit is J/C or Volt.
NOTE:-
(1) Electric field strength can be described in terms of either vector or scalar V
(2) The potential energy of charge at a point where the potential is
is given by
(3) Electric potential difference: The potential difference between two points is an electric field is the amount of work done in bringing a unit +ve charge from one point to another.
i.e.
(4) A common unit of P.E. in atomic physics is eV. . It is the amount of work done when an electron is moved through a p.d. of 1 volt.
(5) if then
i.e. B is at a higher potential and A is at a lower potential (L→H)
if then
if then
i.e. A is at a higher potential and B is at a lower potential (H→L)
(6) +ve charge always flows from higher potential to lower potential.
Electric potential at a point due to a single-point charge
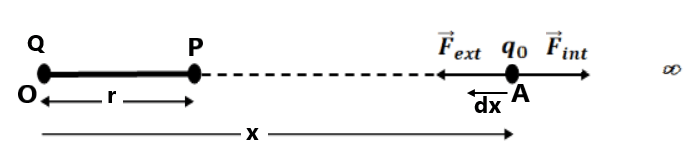
Consider a point charge Q placed at point O. We have to calculate electric potential at point P which is distance r from O. Consider a point A intermediate between ∞ and P.
The electric field on at A due to Q is
∴ external force is the same as but in the opposite direction.
i.e.
∴ work done by this force due to small displacement dx is
(here -ve sign is taken because dx is measured along the -ve direction of x)
∴ Total work done in moving the charge from ∞ to the point P will be
∴ The electric potential at point P is defined as
Note:-
1. If a medium is introduced, the potential at a point is defined as
where dielectric constant
2. at
i.e. at infinite, electric potential is zero
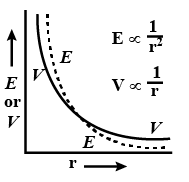
3. For a point charge therefore, the electric field intensity
decreases more rapidly than potential
with increasing distance
.
4. Potential at a point due to a group of point charges
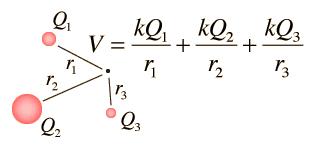
5. The potential near the +ve charge is more than the potential near the -ve charge.
6. Potential due to +ve charge decreases with increasing distance and potential due to -ve charge increases with increasing distance and vice versa.
7. Potential at a point due to continuous charge distribution. ( Use Integration technique)
8. Potential in vector form.
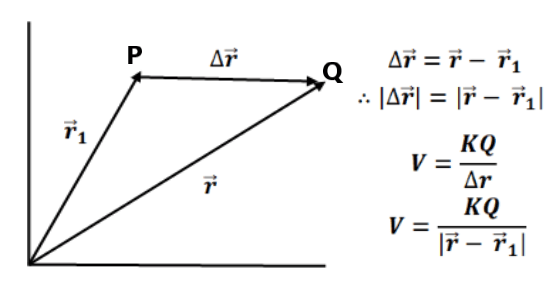
Potential of charges in an external electric field
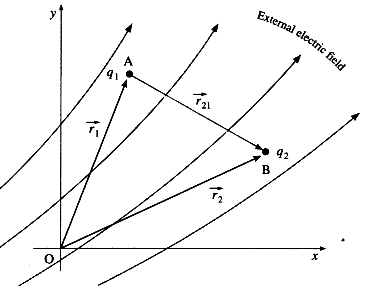
Let us consider two point charges and
placed at points A and B in an external electric field. They are at a distance of
and
from the origin. Let the potential at A is
and potential at B is
respectively.
i.e. work done in bringing a charge from
to point A inside the external electric field is
This is the P.E of charge in the external electric field
i.e.
Similarly, the P.E of charge in an external electric field is
Total P.E of system = Workdone is assembling the two charges
Electric potential due to an electric dipole
Case 1: On the axial line
at P
Case 2: On the equatorial line
at P
Case 3: At any point
Consider a small dipole AB consisting of two charges -q and +q- separated by a small distance 2d. We have to calculate electric potential at any point P which is distance r from center of dipole O.
Let
from the figure, suppose
Draw
Now potential at P due to dipole is
Special Case
(a) When point P lies on the axial line i.e. θ=0° or 180°
(b) When point P lies on the equatorial line i.e. θ=90°
NOTE:-
The electric potential due to point charge is
while for dipole
. Thus the electric potential due to dipole decreases quickly with an increase in distance compared to the potential due to a point charge.
The potential due to a dipole is axially symmetric. If we rotate the observation point P about the dipole axis (keeping r and θ fixed), the potential doesn’t change. However potential due to a point charge is spherically symmetric.
Relation between electric field and electric potential
Suppose, the electric field at a point due to a charge distribution is and the electric potential at the same point is V.
Let a point charge is placed at that point. Force on charge
is
Suppose, due to this force, the charge is displaced slightly
. The work done by electric force (internal force) during this displacement is
By definition, a change in potential energy is given by
we know that
This is the relation between V and E.
Here we can also write
where θ is the angle between
and
Now, Gives the component of the electric field in the direction of
.
Potential gradiant, it is the rate of change of potential with r. -ve sign indicate, V is decreasing in the direction of E.
if ,
i.e., the electric field is along the direction in which the potential decreases at the maximum rate.
From the above relation S.I. unit of an electric field is V/m.
If work done is on the cartesian system, then
and we can write
if y and z are constant, then
if z and x are constant, the
if x and y are constant, then
otherwise
* In uniform electric field
Case 1:-
i.e. Potential drop is
Case 2:-
Finding electric field, if potential is given
We know that
if x co-ordinate is changed from x to x+dx keeping y and z co-ordinate unchanged i.e. dy=dz=0
Similarly,
and
and we can write
Finding potential if electric field is given
Here we can use only
Equipotential surface
Any surface which has the same potential at every point is called an equipotential surface.
Properties of equipotential surface:-
1. The potential difference between any two points of any equipotential surface is zero
2. No work is done in moving a test charge over an equipotential surface.
3. Electric field is always perpendicular to the equipotential surface.
4. Two equipotential surface can never intersect because at the point of intersection there are two values of potential which is impossible.
5. The spacing between equipotential surface enables us to identify region of strong and weak fields.
Electric field due to continuous charge distribution
Self Energy
Earting of a conductor
Behaviour of conductor in electric field
