Work:-
In physics, work has a special meaning. Work is only done by force when the force acting on an object produces displacement in it in the direction of force.
Necessary conditions for work done :
(1) Force on an object (2) The object must be displaced (3) Component of force must be along displacement.
E.x- (1) Pushing the wall by hand but the wall does not move, then w=0
(2) A man holding a bucket of water is walking on a horizontal road, then w=0
Work done by constant force:-
The work done on an object by the constant force is defined as the scalar product ( dot product) of the force and the displacement produced.
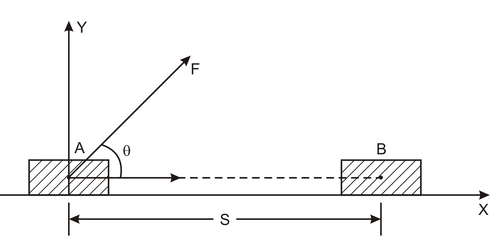
where
is the angle between
It is a scalar quantity and its S.I unit is N-m or Joule. Its CGS unit is Dyne-cm or ergs
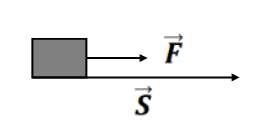
Special Case:
a. if
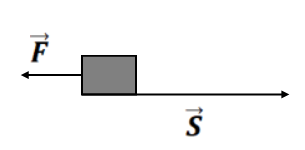
b. if
c.
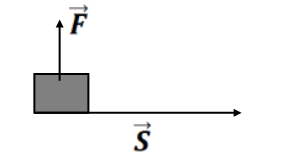
NOTE:-
(a) Between work is +ve and between
work is -ve and at
work is zero
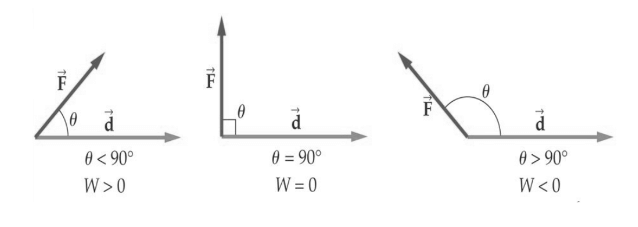
(b) Total work done is equal to the sum of work done by individual forces on body/ system.
(c) Weight of body=50 kgf that means m=50 kg.
(d) -ve work means velocity decreases and +ve work means velocity increases.
(e) If a force is always tangential to the path and its magnitude is constant then work is given by W=±FS where S is the path length (distance)
Ex- 
Exercise 11. How much work is done in pulling a box 2m across a tabletop with a horizontal force of 35N? (70 J) 2. A woman pushes a lawn roller with a force of 180N at an angle of 37° downward from the horizontal. How much work does she do as she pushes the roller a horizontal distance of 50m? 3. A worker does 300 J of work against a frictional retarding force of 15N in pushing a box across a floor in 3 sec. If the box moves with a constant speed, how fast is it going? (6.7 m/s) 4. Find the work done in moving a 50 kg block through a horizontal distance of 10m by applying a force of 100N which makes an angle of 60° with the horizontal. (500 J) 5. A coin of mass m slides a distance D along a tabletop. If the coefficient of friction between the coin and the table is μ, Find the work done on the coin by friction. ( -μmgD) 6. The coefficient of kinetic friction between a 20 kg box and the floor is 0.4. How much work does a pulling force do on the box in pulling it 8m across the floor at a constant speed? The pulling force is directed 37° above the horizontal. (482 J) 7. A 52 kg box rests on the floor. How much work is required to move it at constant speed (a) 12 m along the floor against a frictional force of 150N and (b) 12 m vertically upward? (1.8×10³ J, 6.9×10³ J) 8. How much work is needed to push a 1250 kg car 10 m up a 37 incline at constant velocity? (a) Ignore friction (b) assume the coefficient of kinetic friction is 0.09. 9. A particle moves from position 10. A man cycles up a hill whose slope is 1 in 20. If the mass of the man and bicycle is 150 kg and the man covers a distance of 100m along the incline, calculate the work done by man. (7350 J) 11. A particle moves 4m along z-axis. Find the workdone by the force
|
Exerciseएक्साम्प्ले |
