| Content:- Frictional Force, Spring Force, Impulse, Conservation of Linear Momentum |
Frictional Force
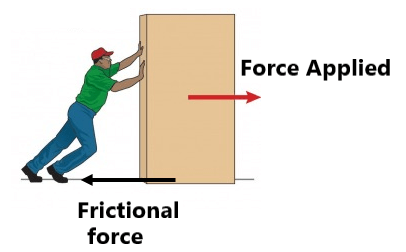
Friction is an opposing force that comes into play when one body moves or attempts to move over the surface of another body. Its direction is always parallel to the surfaces in contact.
According to the modern view, friction is due to the atomic and molecular forces of attraction between the two surfaces at the point of their actual contact.
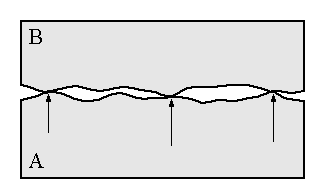
On a microscopic level, even the most polished surface is far from plane i.e. every surface has roughness. Therefore, when two surfaces are put together, the actual area of contact is much less than the actual area of the surface. The pressure at the contact points is very high and the molecules are pushed into such close proximity that the attractive forces between them weld the surfaces together at contact points.
When we try to move one body over another body, these tiny welds oppose motion. This gives rise to the opposing force of friction.
There are three types of sliding friction
- Static friction
- Limiting Friction
- Kinetic Friction
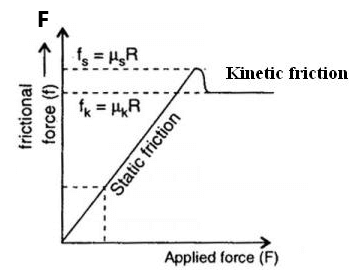
(a) Before the body begins to move, the static friction plays the role; The static friction increases as the applied force increases up to the value of limiting friction ( i.e. maximum static friction)
Static friction is a self-adjustable force with applied external force.
The formula for limiting friction is given by
where coefficient of limiting friction ( or static friction) [ its value depends upon the nature of both surfaces.
Normal force
(b) Once limiting friction is overcome by the applied force, the role of static friction is over. Now smaller friction force ( Kinetic Friction ) opposes the motion.
The formula of kinetic friction is given by
where coefficient of kinetic friction and its value depends upon the nature of both surfaces
(c) Both limiting friction ( ) and kinetic friction (
) are important. The limiting friction must be overcome to start the body moving and then a smaller frictional force opposes the motion.
NOTE
if only is mentioned, it implies
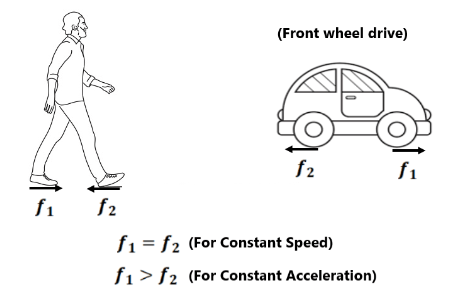
Friction always opposes relative motion. It does not mean friction always opposes motion. In many situations friction gives motion.

Here friction force between A and B gives the motion of A.
The frictional force is proportional to the magnitude of the normal force. i.e.
The frictional force is independent of the size of the contact area between both surfaces.
The frictional force is independent of the velocity of the object. ( speed < 10 m/s )
The frictional force is one component (which is along the surface) of the Contact force.
Example:-
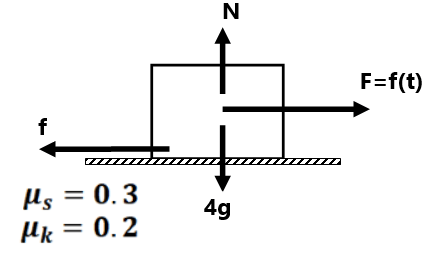
Here
| Applied Force | Frictional Force | Acceleration of Block |
| 0 | 0 | 0 |
| 4N | 4N | 0 |
| 10N | 10N | 0 |
| 12N | 12N | 0 |
| 14N | 8N | 1.5 m/s² |
| 20N | 8N | 3 m/s |
Exercise 1(1) A block of mass 10 kg lying on a horizontal surface just begins to move when a horizontal force of 25 N acts on it. Find (2) Determine the magnitude of frictional force and acceleration of the block in each case.
(3) Find the frictional force. ( mg sinθ)
(4) What maximum force is applied so that the book remains in equilibrium? (25N)
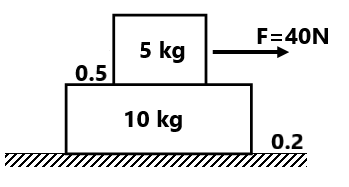
(5) Find the frictional force on the blocks, normal force between the blocks, and acceleration of the block for the following value of applied force F. (a) F= 5N, (b) F=12N, and (c) F=18N ( 5N, 0N, 0N, 0 m/s²)(9N, 3N, 3N, 0 m/s²)(9N, 4N, 6N, 1 m/s²)
(6) Find the tension in the string and acceleration of the block for the following value of m. (a) m= 0.5 kg, (b) 1 kg (c) 2 kg ( 5N, 0 m/s²)(10N, 0 m/s²)( 120/7 N, 10/7 m/s²)
(7) If force is gradually increased from zero. Draw the graph between F and tension T in the string.
(8) Calculate the tension in the string connecting the wall and block if. (a) F= 20N and (b) F=60 N ( 0, 30N)
(9) If the breaking strength of the string in the previous problem is 50N. What maximum force is applied to the body to stay? If we increase force a little bit. What is the acceleration of the block? ( 5.5. m/s²) (10)
(a) What is the maximum value of m, such that it remains in equilibrium? ( 3 kg) (11)
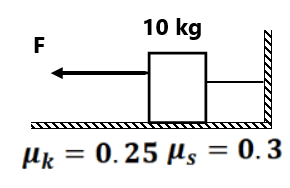
(a) Find the least pulling force that will slide a body on a rough horizontal surface. (12) Force F is gradually increased from zero. Determine whether the block will first slide or lift up. ( begin to slide before lifting)
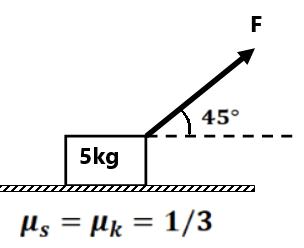
(13) Find the magnitude and direction of friction force. ( 25N, 37°)
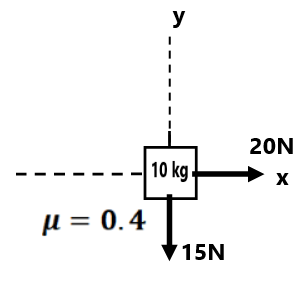
(14) Determine the magnitude of frictional force and acceleration of the block in each of the following cases. ( 30N, 4 m/s²)(50N, 0m/s²)(120N, 5m/s² up)
(15) For what range of values of F, the block remain in static equilibrium.
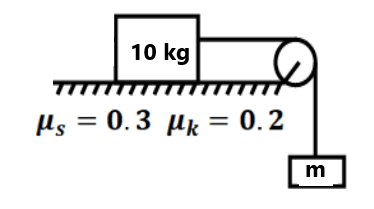
(16) Find the force F to slide B at constant speed in each case. ( 4N, 50N)
|
NOTE
Pulling is easier than pushing on a rough surface:-
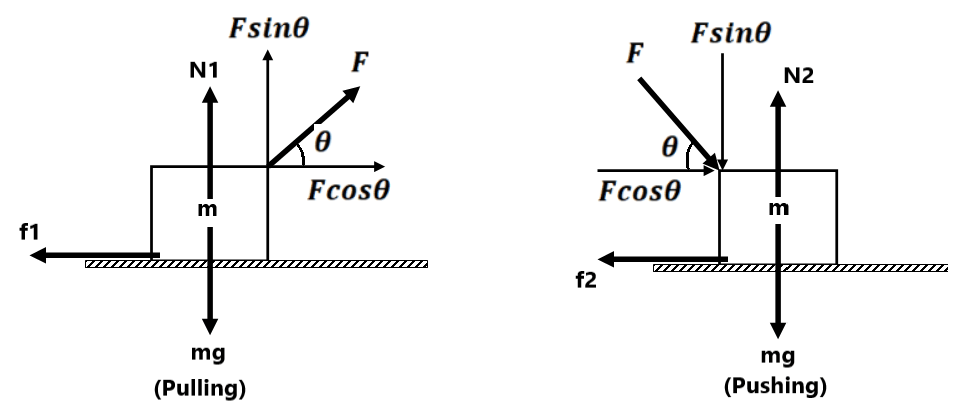
In case of pulling
In case of pushing
In a pulling situation, normal force decreases, therefore frictional force decreases.
Contact Force:-
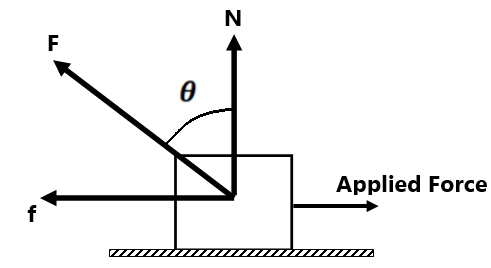
From, Fig F is a contact force.
The component of contact force parallel to the surface is frictional force and perpendicular to the surface is normal force.
Now, and
In the case of limiting friction, θ is called the ” angle of friction “
(a) If the block is kept on a rough horizontal surface, i.e. in this case
so contact force
(b) If the block is moving on a rough horizontal surface, i.e. in this case
so contact force
Body on a rough inclined plane
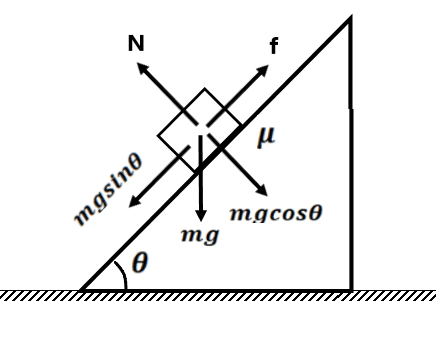
From fig
(a) If
then frictional force is and the block stays in equilibrium
(b) If the angle is increased, then at some value of block just tends to slide but the block stays in equilibrium
is called the ” angle of repose.”
(c) if
Then the block is in accelerated motion.
Now,
Here acceleration is independent of mass, it depends on . Lesser the value of
, more is the acceleration.
Minimum Force required to move a body:-
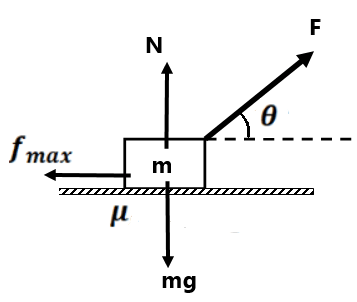
From fig,
also
For the minimum value of
Solving it, we get
which is the same as the angle of friction
i.e. if we pull the block at an angle equal to the angle of friction then the applied force is minimum and
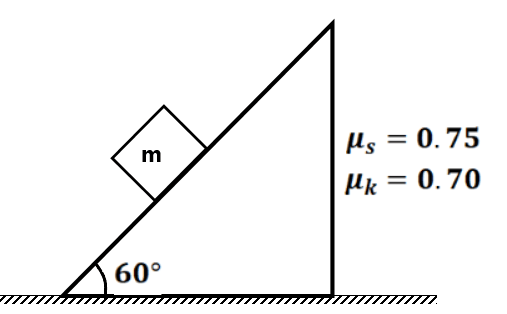
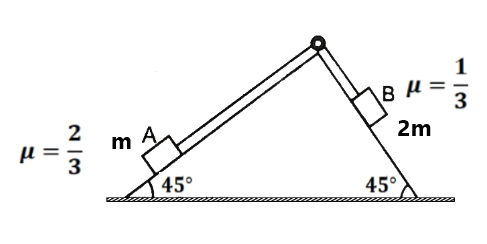
Exercise 2(1) A block of mass is placed on a rough inclined plane. The block will slide or not. (slide)
(2) Find the range of mass of block B so that the system stays in equilibrium. ( 2 kg≤m≤4 kg )
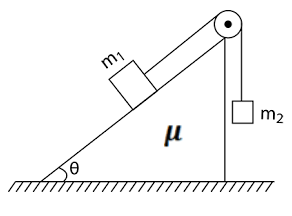
(3) Find the mass ratio (m2/m1) at which the body m2
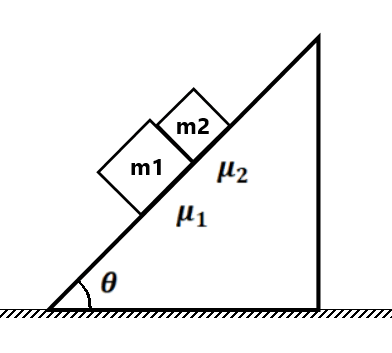
(a) Starts coming down (4) Find the acceleration of the block of mass m1 and m2. if (a) μ1>μ2 (b) μ1<μ2
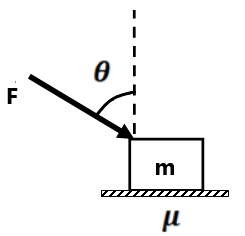
(5) A block placed on a rough horizontal surface is being pushed by a force F making an angle θ with the vertical. If the friction coefficient is μ, how much force is needed to get the block just started? Discuss the situation when tanθ<μ
(6)
(a) What maximum horizontal force F can be applied without disturbing the equilibrium of the system? (7)
(a) Find the acceleration of A if the system is released from rest. (0)
|
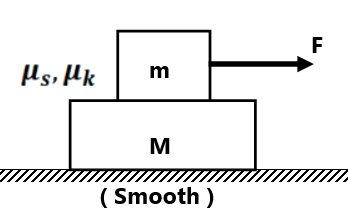
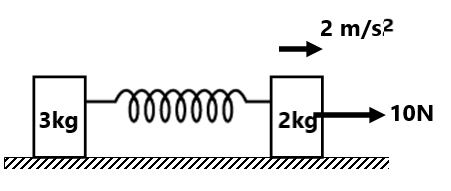
Two and Three blocks system
Exercise(1) Find the acceleration of the blocks and frictional force between them for the following values of force F (g=10 m/s²) (a) F=5N (b) F=10N (c) F=15N (d) F=20N ( 2N,1 m/s², 4N, 2 m/s², 4N, 3 m/s², 6N, 3m/s²,14/3m/s²)
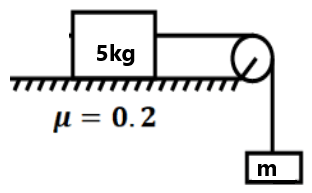
(2) Find the acceleration of the block if μ=0.5 is the same for any surface. (a=0, a= 2.5 m/s²)
(3) Find the acceleration of blocks if F is (a) F=2N (b) F=4N (c) 6N (d) 8N
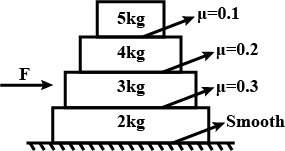
(4) Find the acceleration of the two-block system and frictional force between all contact surfaces.
(5) Find the acceleration of blocks, if F=40N ( 3 m/s², 0 m/s²)
(6)
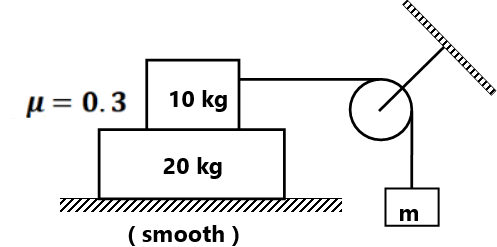
(a) What is the maximum possible value of F so that the system moves together? (7)Find the maximum value of m so that there is no relative motion between 10 kg and 20 kg. ( 90/17 kg)
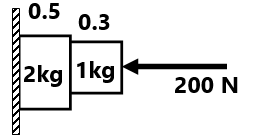
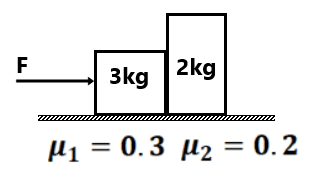
(8) Find the frictional force acting between the wall and the 2kg block.
(9) Find the acceleration of blocks and frictional forces acting on the blocks for the following cases. (a) F=5N, (b) F= 10N, (c) F=15N, (d) F=18N, (e) F=25N
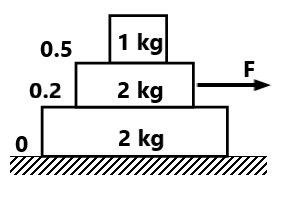
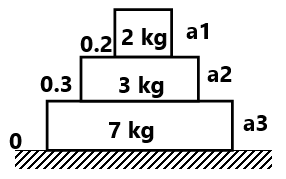
(10) Find the acceleration a1,a2 and a3 of the three blocks shown in fig. If horizontal force 10N is applied on (a) 2kg block (b) 3 kg block and (c) 7 kg block take g=10m/s². ( 3 m/s² 0.4m/s² 0.4 m/s², 5/6 m/s² 5/6m/s², 5/6 m/s², 5/6 m/s²)
(11) In the figure friction coefficients and masses are given. We applied a force on block. What is the maximum force we can apply for common acceleration? (14N)
|
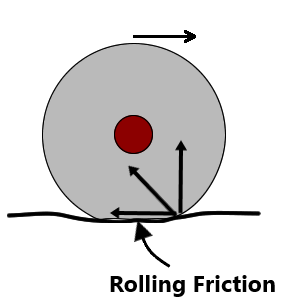
Rolling Friction:
When one body rolls over another, the resistance offered to motion is called rolling friction. In rolling, at every instant, there is just one point of contact between the body and the plane and this point has no motion relative to the plane. In this ideal situation, kinetic or static friction is zero and the body should continue to roll with constant velocity.
But in practice, this will not happen and some resistance to motion does occur, this resistance force is known as rolling friction. i.e. to keep the body rolling, some applied force is needed. Its magnitude is very much smaller than sliding friction.
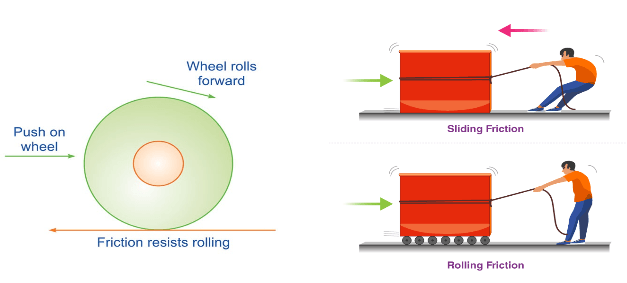
Cause:- During rolling, the surfaces in contact get momentarily deformed a little, and this results in a finite area ( not a point) of the body being in contact with the surface. The net effect is that the component of the normal force parallel to the surface opposes motion.
Advantages and Disadvantages of friction
Advantages:-
- It is due to friction between the ground and the feet that we are able to walk.
- The breaks of friction vehicle cannot work without friction.
- Pulleys are able to rotate because of friction between the belt and the pulley.
- The tires of the vehicle are made rough to increase friction.
- In the absence of friction, it will not be possible to write on paper with a pen or pencil.
- Due to friction, we are able to hold the body.
- Due to friction, nails are fixed inside the wood.
Disadvantages:-
- Wear and tear of the machinery is due to friction.
- A large amount of power is wasted in overcoming friction and the efficiency of the machine decreases considerably.
- Excessive friction between rotating parts of a machine produces enough heat and causes damage to the machinery.
Methods of reducing and increasing friction
We can reduce friction by
- Polishing
- Lubrication:- It is a substance ( solid, liquid, or gas) that forms a thin layer between two surfaces in contact. (oil, grease, etc)
- Stream Lining:- Friction is reduced due to air, and water by streamlining the shape of the body.
- Using ball- bearing:- ( sliding friction is converted into rolling friction)
We can increase friction by
- The treading of tyres is done to increase friction between the road and the tyres.
- Sand is thrown on tracks covered with snow or clay.
SPRING FORCE
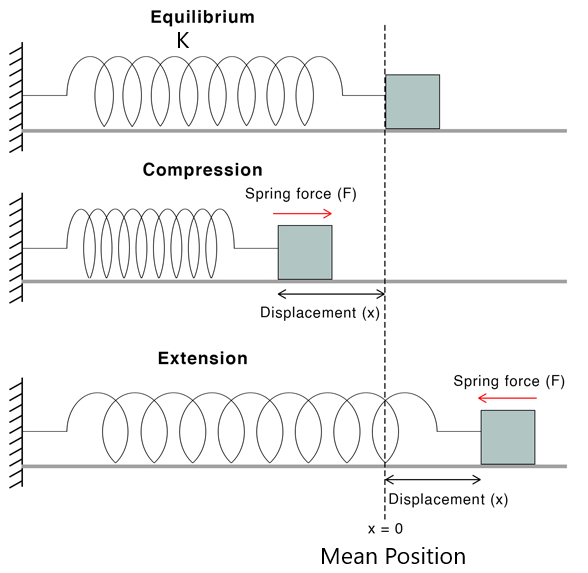
It obeys Hooke’s law within the elastic limit. The restoring force produced in the spring is proportional to deformation produced in the spring.
i.e
(
is elongation or compression on spring)
where k is the constant known as force constant or spring constant or stiffness of spring, and its value depends upon the nature of the material and its geometrical construction.
-ve signs indicate are opposite to each other.
NOTE
- For massless spring force in different parts will be the same.
- If a massless spring is attached to a massless string, then the tension and spring force on the spring are taken same.
- The force of spring doesn’t change instantaneously.
- The force constant of spring is inversely proportional to its natural length. i.e.
Ex- An ideal spring is cut into three different parts in a ratio of 1:2:3. If the spring constant of the original spring is k. What is the spring constant of the three parts?
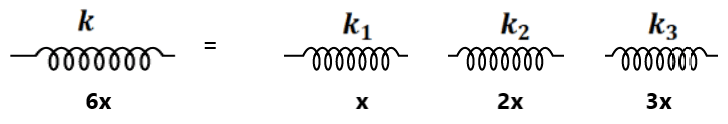
We know that
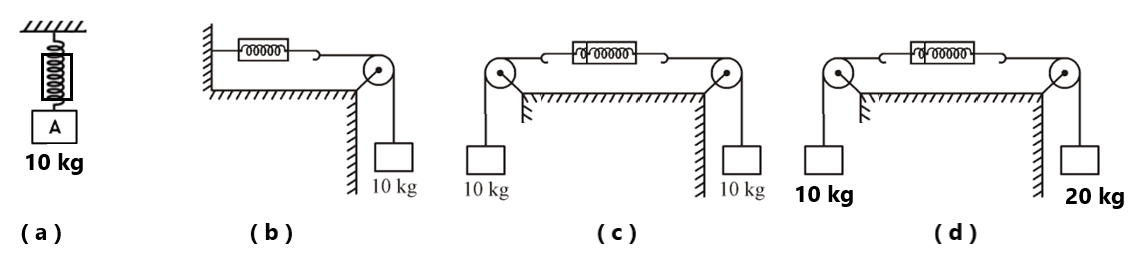
Exercise(1) What is the reading of the spring balance in the following situations? ( in three cases reading= 10kg, 40/3 kg)
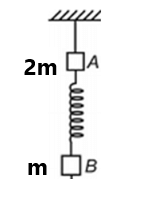
(2) Two blocks are connected by a spring. The combination is suspended, at rest, from a string attached to the ceiling as shown. The string breaks suddenly. Immediately after the string breaks, what is the initial downward acceleration of the upper block of mass 2m? (3g/2)
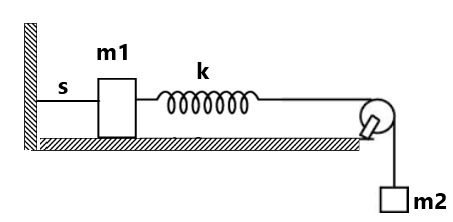
(3) In the following fig. The right end of each spring is pulled by a force that is increased gradually from zero to F. Extension in these springs are
(4) A smooth block of mass m is connected with a spring of stiffness k (=20 N/m) and natural length l’=0.25 m. If the block is pulled such that the new length of the spring becomes l=0.3 m, find the acceleration of the block at the moment when it is released from the given position. (1 m/s²) (5) Find the acceleration of blocks A and B just after the string is cut. (2g downward, 0)
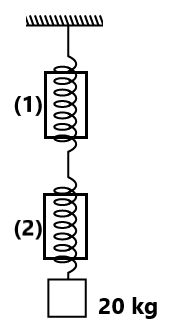
(6) Calculate the reading of spring balance (1) and spring balance (2) (20 kg)
(7) Find the acceleration of the blocks A, B, and C, all of equal mass m at the instant when
(a) The spring between ceiling and A is cut. ( 15 m/s², 15 m/s²,0) also find the tension in the string in the above three cases.( mg/2, 0, 3mg/2) (8) Two blocks are connected by a spring of a natural length of 2m. The force constant of spring is 200 N/m.
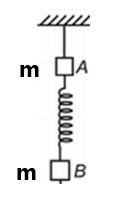
Find the spring force in the following situations: (a) A is kept at rest and B is displaced by 1m in the right direction. (200N) (9) Find the acceleration of blocks A and B just after the string is cut. ( g up, g down)
(10) Find the acceleration of 3 kg mass when the acceleration of 2 kg mass is 2 m/s² as shown in Fig ( 2 m/s²)
(11) Find the reading of spring balance as shown in Fig Assume that mass M is in equilibrium. ( all surfaces are smooth) (12N)
(12) Find the acceleration of the bodies just after the string S is cut. ( all surfaces are frictionless)
(13) An ideal spring of constant k is cut into n identical parts. What is the spring constant of each part? ( nk) |
IMPULSE
When two bodies collide, they exert force on each other while in contact. The momentum of each body is changed due to the force on it exerted by the other. On an ordinary scale, the time duration of this contact is very small, and yet the change in momentum is sizeable.
This means that the magnitude of the force must be large. Such large forces acting for a short duration are called impulsive forces. The force may not be uniform while the contact lasts.
The change in momentum produced by such an impulsive force is
On the right side of the expression i.e. which is the area under (F-t) curve in 1D motion is known as an impulse of the force
during the time interval
to
.
Impulse is not a property of a particle, rather, it is a measure of the degree to which an external force changes the particle’s momentum.
Impulsive Force
The force which acts on bodies for a short time is called impulsive force. Ex- A bat hitting the ball, Collision of two billiard balls, The firing of a gun, etc
The impulsive force is not constant but varies with time. Therefore, it is not easy to measure the impulsive force. In such cases, we measure the total effect of the impulsive force called impulse.
An impulse of a force is the product of the average force during the impact and the time for which the impact lasts. i.e.
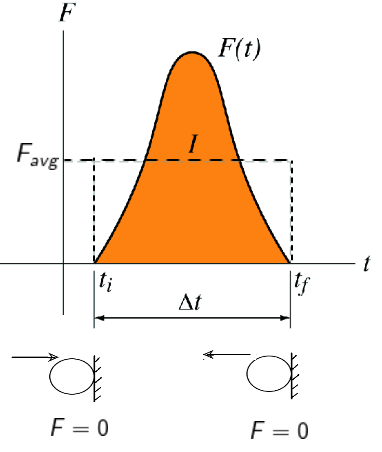
Impulse is a vector quantity and its direction is the same as where momentum is changed. Its S.I unit is N-s of Kg-m/s
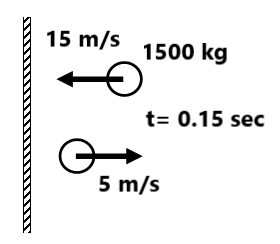
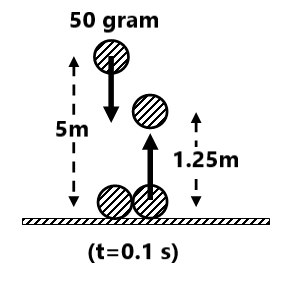
Exercise 1(1) A body of mass 0.25kg moving with a velocity of 12 m/s is stopped by applying a force of 0.6N. Calculate the time taken to stop the body. Also, calculate the impulse of this force. ( 5 sec, -3.0 N-s) (2) A ball of mass 10 grams hits a hard surface vertically with a speed of 5 m/s and rebounds with the same speed. The ball remains in contact with the surface for 0.01 seconds. Find the average force exerted by the surface on the ball. ( 10N) (3) Find the impulse caused by the collision and the average force exerted on the block.
(4) Find the impulse and the average force between the ball and the ground. (0.75 j Ns, 7.5 N)
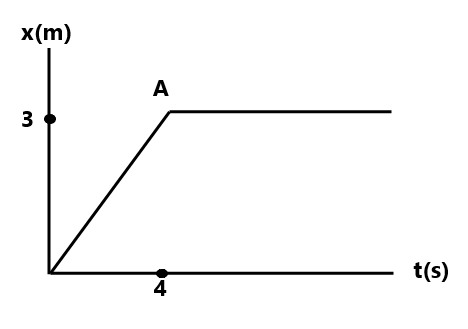
(5) Fig shows the position-time graph for the 1D motion of a particle of mass 4 kg.
What is the (a) Force on the particle for t<0, t>4 sec, 0<t<4 sec ( 0 in all cases) |
CONSERVATION OF LINEAR MOMENTUM
We know that from Newton’s 2nd law
For an isolated system,
i.e.
It means ” If no external forces act on a system, the linear momentum of the system will remain constant. This is known as the principle of conservation of linear momentum”
Practical Application:
- When a bullet is fired from a gun, the gun recoils backward.
- When a man jumps from a boat to the shore, the boat slightly moves away from the shore.
- A rocket works on the principle of conservation of linear momentum.
- If an astronaut in open space, away from a spaceship, wants to return to his space, he can do so by throwing something in a direction opposite to that in which the spaceship is moving.
Exercise(1) What is the recoil velocity of a 2kg gun if it shoots a 7-gram bullet out of the muzzle at a speed of 500 m/s? ( -1.75 m/s²) (2) A 30 kg shell is flying at 48 m/s. When it explodes, its one part of 18 kg stops while the remaining part flies on. What is the velocity of the latter? (120 m/s) (3) A neutron having a mass (4) A bomb at rest explodes into three fragments of equal masses. Two fragments fly off at right angles to each other with velocity 9 m/s and 12 m/s respectively. Calculate the speed of the third fragment. ( 15 m/s) (5) A machine gun of mass 10 kg fires 20-gram bullets at the rate of 10 bullets per second with a speed of 500 m/s. What force is required to hold the gun in position? ( 100N) (6) A hunter has a machine gun that can fire 50-gram bullets with a velocity of 150 m/s. A 60 kg tiger springs at him with a velocity of 10 m/s. How many bullets must the hunter fire into the tiger in order to stop him on track? ( 80) (7) A hunter fires a bullet of mass 10 grams with a velocity of 400 m/s from a gun of mass 5 kg. What will be the recoil velocity of the gun? If the hunter is standing on ice, then what velocity he ( along with the gun) will acquire? mass of the hunter is 75 kg. ( 0.8 m/s, 0.05 m/s) |
Rocket Propulsion ( Example of Variable mass)
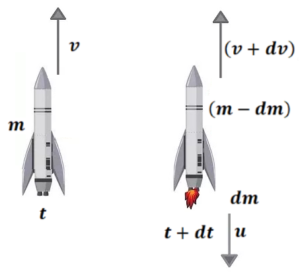
Let at any time t
Mass of Rocket=m
Speed of Rocket=v
After time dt, dm mass of gas is ejected with speed u ( w.r.t. earth)
Then mass of rocket = (m-dm)
Mass of rocket = (v+dv)
Here speed of gas w.r.t. rocket is constant which is the property of the engine of the rocket. Let this speed is
We know that
From the conservation of linear momentum
Thrust on the Rocket:- It is the force with which the rocket moves Forward.
From equation (1)
divide both sides by , we get
Here F is the thrust of the rocket at time t.
i.e. we can say that “Thrust on the rocket at any instant is equal to the product of the exhaust speed of the burnt gases and the rate of consumption of fuel at that instant.”
Velocity of the Rocket at any time :-




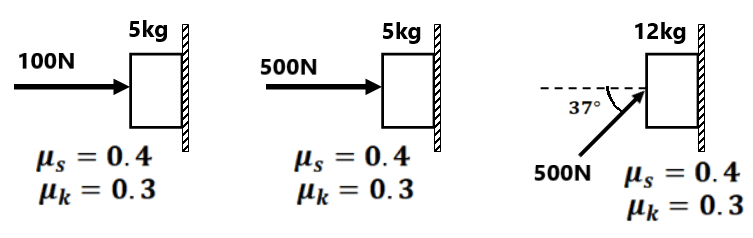
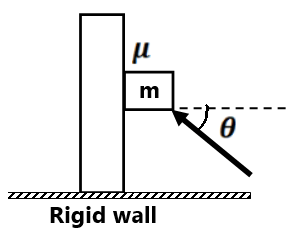




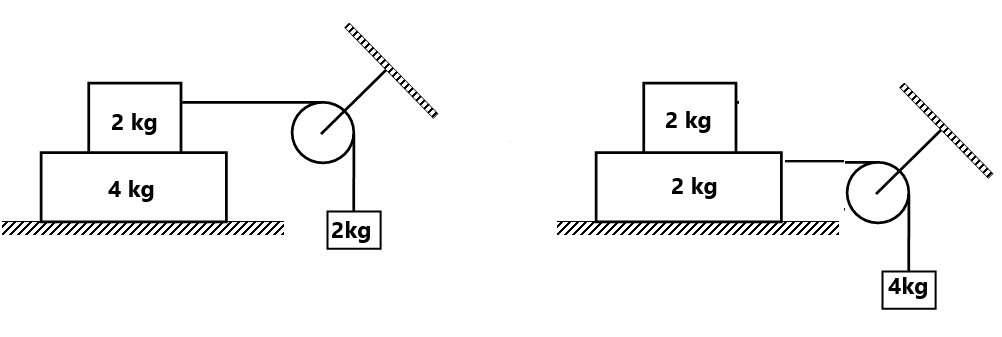
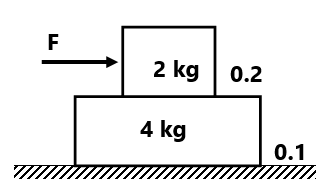 ( 0 m/s², 0 m/s²)(0 m/s², 0 m/s²)(1 m/s², 0 m/s²)
( 0 m/s², 0 m/s²)(0 m/s², 0 m/s²)(1 m/s², 0 m/s²)