हाइगेन्स के अनुसार
- प्रकाश एक यांत्रिक तरंगें ( Mechanical wave) है जिसे संचरण के लिए माध्यम की आवश्यकता होती है । हाइगेन्स ने एक काल्पनिक माध्यम ‘ ईथर ‘ की कल्पना की जिसका घनत्व बहुत कम तथा प्रत्यास्था बहुत अधिक होती है , जो सभी जगह समान रूप से व्याप्त है ।
- प्रकाश एक अनुदैर्घ्य तरंग ( Longitudinal wave ) है जिसमे माध्यम के कण का कम्पन , तरंग के संचरण की दिशा की और होती है ।
मैक्सवेल के अनुसार
- प्रकाश एक विधुत चुम्बकीय तरंगें ( Electro Magnetic Wave) है जिसे संचरण करने के लिए किसी माध्यम की आवश्यकता नहीं होती है ।
- प्रकाश एक अनुप्रस्थ तरंग ( Transverse Wave) है जिसमे विधुत क्षेत्र के घटक तथा चुम्बकीय क्षेत्र के घटक एक दूसरे के लम्बवत होती है, जो ज्या वक्रीय ( Sine Curve) में दोलन करते है तथा यह दोलन तरंग के संचरण की दिशा के भी लम्बवत होती है ।
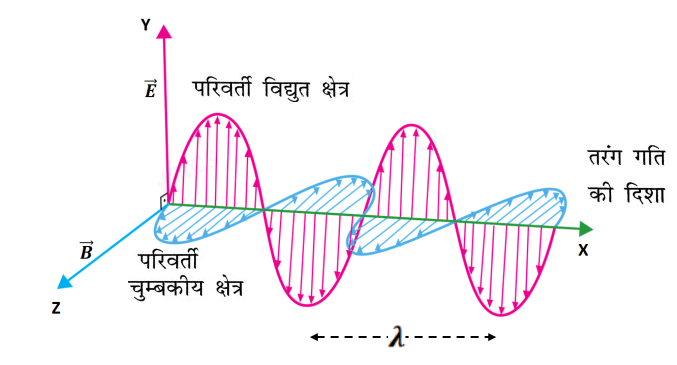
NOTE:- प्रयोग से यह पाया गया की प्रकाश के संचरण के लिए मुख्यतः विधुत क्षेत्र के घटक ही उत्तरदायी है । अर्थात प्रकाश के कम्पन का अर्थ , विधुत क्षेत्र के घटक का कम्पन है ।
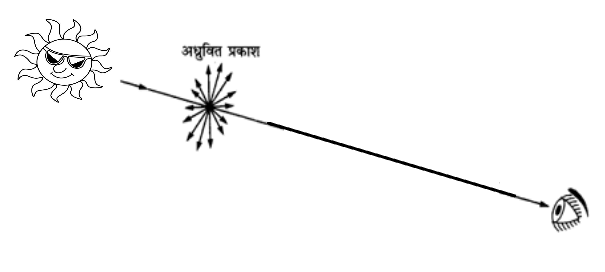
अध्रुवित प्रकाश (Unpolarised Light) :-
साधारण प्रकाश अध्रुवित प्रकाश होती है । अध्रुवित प्रकाश में विधुत क्षेत्र के घटक, प्रकाश के संचरण की दिशा के लम्बवत सभी दिशाओं में समान रूप से कम्पन करती है ।
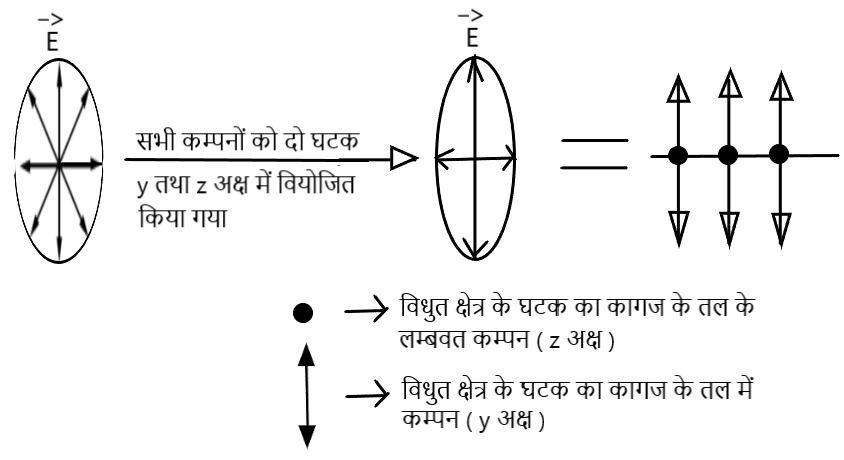
ध्रुवण (Polarisation)
यदि किसी प्रक्रिया द्वारा प्रकश स्रोत से निकलने वाले विधुत क्षेत्र के घटक के कम्पनों को तरंग संचरण की दिशा के लम्बवत एक निश्चित दिशा या तल में सीमित कर दिया जाये तो इस घटना को प्रकाश का ध्रुवण कहते है ।
तथा ध्रुवण के बाद प्राप्त प्रकाश को ध्रुवित प्रकाश कहते है । अर्थात अध्रुवित प्रकाश को ध्रुवित प्रकाश में बदलना प्रकाश का ध्रुवण कहलाता है ।
अध्रुवित प्रकाश को पोलराइड के सहायता से ध्रुवित प्रकाश में बदला जाता है ।
पोलराइड / पोलराइजर / टूरमैलीन क्रिस्टल :-
यह एक ऐसा उपकरण है जिसका उपयोग समतल ध्रुवित प्रकाश उत्पन्न करने में होता है । इसके अणुओं की एक दीर्घश्रृंखला होती है जो एक विशेष दिशा में संरेखित होती है ।
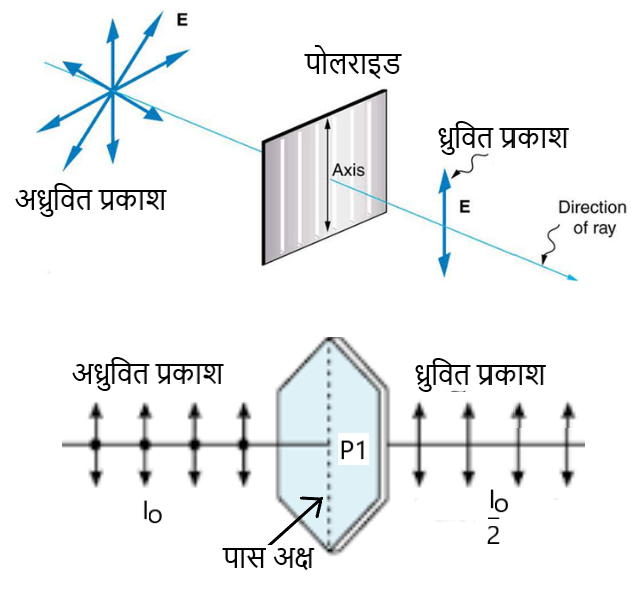
यहाँ पर प्रकाश के विधुत क्षेत्र के वो घटक जो पास अक्ष के अनुदिश हो पोलराइड में प्रवेश कर जाते है ।
प्रकाश के अनुप्रस्थ प्रकृति का सत्यापन
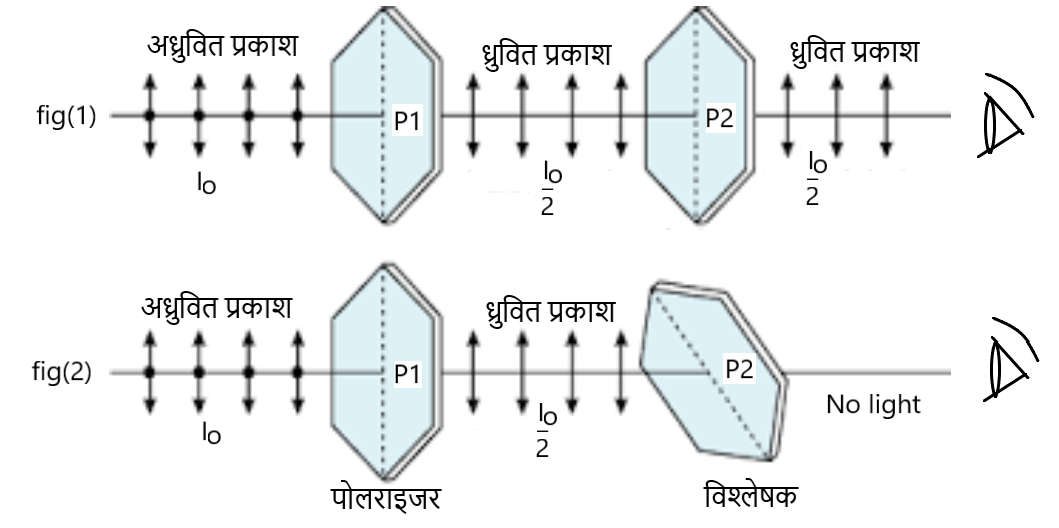
चित्र के अनुसार एक पोलेराइड P1 तथा एक विश्लेषक P2 को एक दूसरे के सामने रखा जाता है ।
चित्र(1) में इन क्रिस्टलों को इस प्रकार रखा जाता है की इन दोनों का पास अक्ष एक दूसरे के समांतर हो । जब अध्रुवित प्रकाश जिसकी तीव्रता है , को P1 तथा P2se पास कराया जाता है तो हमें विश्लेषक P2 द्वारा एक ध्रुवित प्रकाश मिलता है जिसकी तीव्रता वास्तविक प्रकाश की आधी
होती है ।
लेकिन चित्र (2) के अनुसार यदि P1 तथा P2 का पास अक्ष एक दूसरे के लंबवत हो तो हमें P2 द्वारा किसी भी प्रकार का प्रकाश नहीं मिलता है अर्थात तीव्रता शून्य होता है ।
इस प्रयोग से यह निष्कर्ष निकलता है की यदि प्रकाश अनुदैर्घ्य तरंग होती तो दोनों स्थितियों में P2 द्वारा प्राप्त प्रकाश की तीव्रता में कोई परिवर्तन नहीं होता है । प्रकाश के अनुप्रस्थ प्रकृति के कारण ही जब P2 को घुमाया जाता है तो हमें प्रकाश की तीव्रता में परिवर्तन देखने को मिलता है ।
अतः प्रकाश तरंग एक अनुप्रस्थ तरंग है ।
मेलस का नियम
इस नियम के अनुसार जब पूर्ण ध्रुवित प्रकाश को किसी विश्लेषक पर डाला जाता है , तो विश्लेषक से बाहर निकलने वाले प्रकाश की का मान के समानुपाती होता है , जहाँ
विश्लेषक और पोलराइड के पास अक्ष के बीच का कोण है । अर्थात
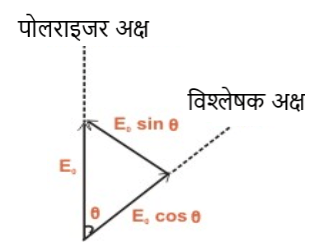
चित्र से साफ़ पता चलता है की केवल घटक ही विश्लेषक द्वारा पार हो रही है । अतः विश्लेषक द्वारा प्राप्त प्राकाः की तीव्रता होगी
समीकरण (1) तथा (2) से
जब तब
( महत्तम )
जब तब
( न्यूनतम )
प्रकीर्णन द्वारा प्रकाश का ध्रुवण
जब अध्रुवित प्रकाश ऐसे माध्यम में संचरण करती है , जिसके कणों का आकर प्रकाश की तरंगदैर्घ्य की अपेक्षा बहुत ही कम होता है । तब प्रकाश इन कणों के द्वारा अवशोषित हो जाते है तथा यह सभी दिशाओं में विकिरित कर दिए जाते है । यह घटना प्रकाश का प्रकीर्णन कहलाता है ।
कुछ प्रकीर्णित प्रकाश का आंशिक ध्रुवीकरण , कुछ का पूर्ण समतल ध्रुवीकरण तथा कुछ का अध्रुवीकरण होता है । यह इस बात पर निर्भर करता है की प्रकाश का प्रकीर्णन किस दिशा में हुआ है ।
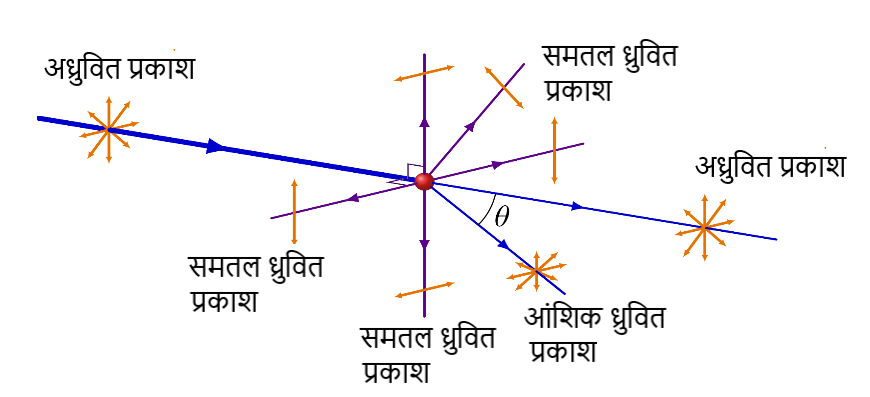
यहाँ पर माना की अध्रुवित प्रकाश x अक्ष की ओर गमन कर रही है । x दिशा में प्रकीर्णित प्राकाः का ध्रुवीकरण नहीं होता है । प्रकाश की दिशा के लम्बवत प्रकीर्णित प्रकाश का पूर्ण समतल ध्रुवीकरण होता है। अन्य सभी दिशाओं में प्राप्त प्रकाश का आंशिक ध्रुवीकरण होता है ।
परावर्तन द्वारा प्रकाश का ध्रुवण तथा ब्रूस्टर का नियम
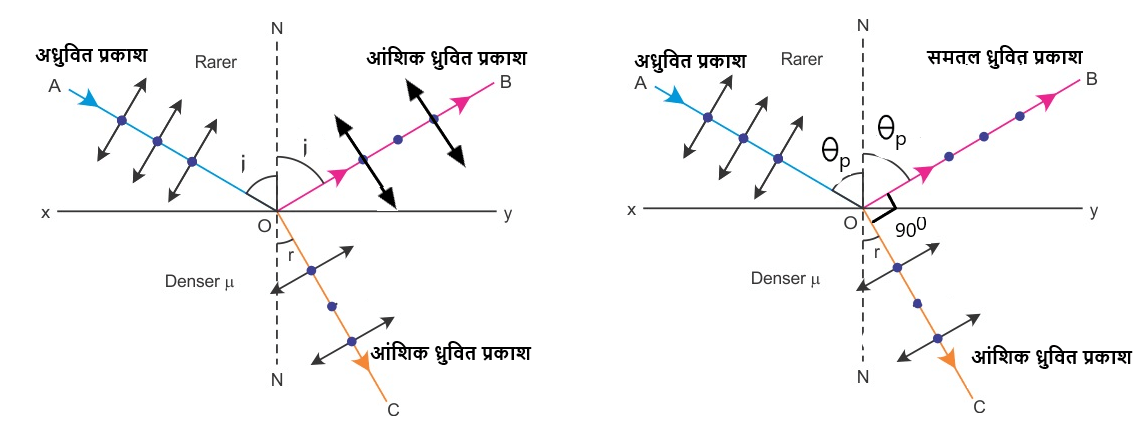
जब अध्रुवित प्रकाश किसी कांच के टुकड़े पर तिरछा आपतित होता है तब यहाँ आंशिक रूप से परावर्तन तथा अपवर्तन होता है । यहाँ पर दोनों, परावर्तित तथा अपवर्तित प्रकाश का आंशिक रूप से ध्रुवण हो जाता है ( चित्र 1)। लेकिन परावर्तित प्रकाश का आंशिक ध्रुवीकरण , पूर्ण समतल ध्रुवीकरण या पूर्ण अध्रुवीकरण होना इस बात पर निर्भर करता है की आपतन कोण कितना है ।
यदि आपतन कोण 0° या 90° हो तो परावर्तित प्रकाश का किसी भी प्रकार का ध्रुवण नहीं होता है । यदि आपतन कोण 0° और 90° के बीच हो , तो हमें अलग अलग मान के ध्रुवित परावर्तित प्रकाश प्राप्त होंगे ।
एक विशेष आपतन कोण पर परावर्तित प्रकाश पूर्णतः समतल ध्रुवित हो जाता है । इस कोण को ध्रुवण कोण या ब्रूस्टर कोण कहते है । तथा इस अवस्था में परावर्तित किरण तथा अपवर्तित किरण एक दूसरे पर लंबवत होती है ( चित्र 2)
ब्रूस्टर का नियम :- इस नियम के अनुसार यदि प्रकाश ब्रूस्टर कोण से किसी सतह पर आपतित होती है तो उस माध्यम का अपवर्तनांक संख्यात्मक रूप से उसके ध्रुवण कोण
के tangent के समानुपाती होती है , अर्थात
चित्र के अनुसार ,
स्नेल के अनुसार
