| Content:- Newton’s Law of Motion, Fundamental forces in nature, Free Body Diagram, Constraints Relation, Pseudo Force |
Simply we know that force means PUSH or PULL
A force can (a) cause linear motion (b) cause rotation (c) deform bodies
From common experience for a body
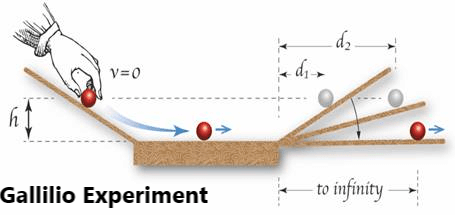
Initially, people knew that all these situations whether it is rest, uniform motion, or accelerated motion are different.
But Gallilio corrected it on the basis of his simple theory and experiment.
The first question that came to people’s minds was
Q > Is an external force required to keep a body in uniform motion?
Ans > According to Aristotle, yes! Aristotle made observations from practical experiences and came to the conclusion that an external force is required to keep a body in uniform motion. This is known as Aristotle’s Fallacy.
But actually, to keep a body in uniform motion, no net external force is required. But the question is still, why does a toy car require an external force to keep it going?
The correct answer to this question given by Galileo in the seventeenth century, was the foundation of Newtonian Mechanics (Inertia Concept). According to him, opposing forces such as friction and viscous force are always present in the natural world. This explains why forces by external agencies are necessary to overcome these opposing forces to keep bodies in uniform motion.
|
|
Aristotle said this misconception was because he argued by looking at everyday events.
Now, on the basis of Gallilio’s theory and experiment, it was revealed that both rest and uniform motion are in the same state, which does not require any external force to maintain it.
i.e. according to Gallilio, the body itself can not change the state of motion of rest or uniform motion. This is called the “Property of Inertia”

” i.e. to change the velocity, force must be required “
◊ INERTIA (Resistance to Change)
It is the property of a body. the tendency of a body to maintain its state of rest or uniform motion in a straight line is called the Inertia of the body. i.e. ” due to Inertia body has resistance to change its state.”
In other words, objects do not change their state of rest or uniform motion unless acted upon by some net external force.
Types of inertia
a. Inertia at rest:- It is the inability of a body to change itself to the state of rest.
b. Inertia at motion:- It is the inability of a body to change itself to a state of uniform motion.
c. Inertia of direction:- is the inability of a body to change by itself the direction of motion.
Example of the law of inertia
- When a train suddenly starts, the passengers tend to fall back.
- When a moving bus is suddenly stopped, the passengers’ tend to fall forward.
- When we beat a carpet with a stick, dust particles are removed.
- When we shake a mango tree, the mangoes fall down.
- An athlete runs some distance before executing a long jump.
- The mud from the wheels of a moving vehicle flies of tangentially.
◊ NEWTON’S FIRST LAW (LAW OF INERTIA)
Every body continues in its state of rest or uniform motion in a straight line, unless it is compelled, by some external force to change that state. i.e. if no net force acts on a body, then the acceleration of a body is zero.
This law is also known as the “law of inertia”. According to this law, a state of rest and a state of constant velocity are equivalent.
Linear Momentum
This is also known as the Effect of force on motion.
Momentum will tell us, how much of an impact (Force) he will make on anyone. The linear momentum of a body is the product of mass m and its velocity v. It is denoted by P.
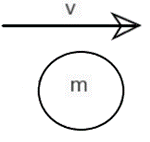
i.e.
It is a vector quantity and its S.I unit is kg m/s.
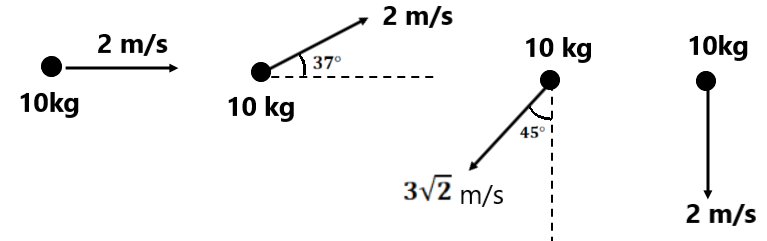
Exercise 1(1) Find the linear momentum of the following in vector form.
(2) Find the change in linear momentum in each case (Magnitude+direction)
|
NOTE (Before starting Newton’s 2nd law)
About Mass
About Velocity ( Only magnitude)
About Velocity ( Only Direction)
About time
The first three are the concept of change in momentum to produce force. These qualitative observations lead to the second law of motion expressed by Newton as follows |
Newton’s Second Law
According to this law, the rate of change of linear momentum of a body is directly proportional to the external force applied on the body and this change takes place always in the direction of the force applied.

i.e. from Newton’s 2nd law
where k is proportionality constant and its value depends on the choice of unit for the force. In S.I unit
Force is a vector quantity and its S.I unit is kgm/s² or Newton(N). Its C.G.S unit is Dyne
Another unit of force that is widely used is Kgf (Kilogram-force). It is a Gravitational unit of force ( 1kgf=9.8N)
Kgf:- The force with which the earth attracts a 1 kg body towards its center is called kilogram force.
i.e. 1 Kgf=mg=1×9.8=9.8N
NOTE:-
The first law gives only the definition of force but does not explain its value. It is 2nd law
The force depends on the time rate of change in momentum, not on momentum.
for instantaneous
if m is constant
The original form of Newton’s 2nd law is
1 Newtons is that force which produces an acceleration of 1 m/s² in a mass of 1 kg.
From Newton’s 2nd law (F=ma) if F=0, then a=0. which is the same as Newton’s 1st law. Therefore, 2nd law is consistent with the first law.
as
i.e. the slop at a point on momentum vs. time graph gives force at that point
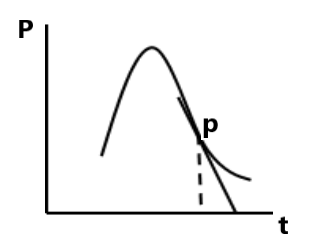
i.e. in (F-t) graph, the area under the time axis gives the change in momentum
The net force will change only that component of the velocity which is in the direction of force.
This law applied to point masses and Centre of mass ( for extended bodies) only.
Forces → (a) Contact force: (Normal force, frictional force, tension force, buoyancy force, etc.)
→ (b) Non-contact force: (Gravitational force, magnetic force, electric force, etc.)
Force ( for system)
→ (a) Internal force: Forces between internal bodies of the system. The sum of all internal forces is always zero.
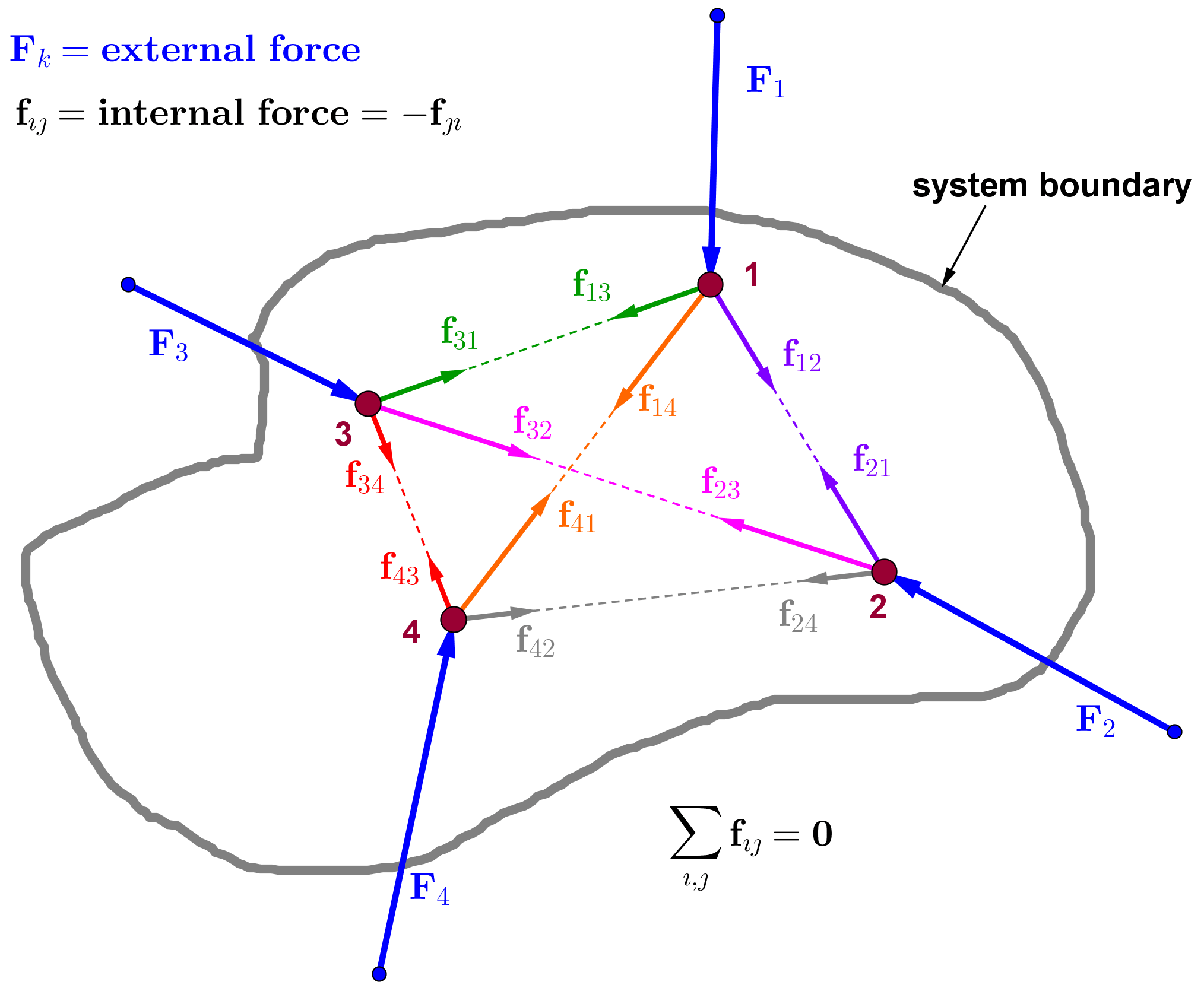
→ (b) External force: Forces on a system by an external agent (If no external force acts on a system, the system is known as an “isolated system”)
From Newton’s 2nd law
Here F is the total forces acting on a system
i.e.
means total external force on a system
i.e. we can write
We know that
Here force does not depend only on change in momentum, but force also depends on how fast/ slow this momentum changes.
- A seasoned cricketer draws in his hand during a catch, allowing greater time for the ball to stop and hence requires a smaller force.
- To avoid jerks in vehicles, a spring is placed in the wheel.
- Jumping from a height onto a concrete floor is more likely to cause injury while jumping on the sand doesn’t hurt much.
Exercise 2(1) What is the acceleration of an astronaut when he is outside the spaceship? (2) Find the average resistance force exerted by the block on the bullet. (270 N)
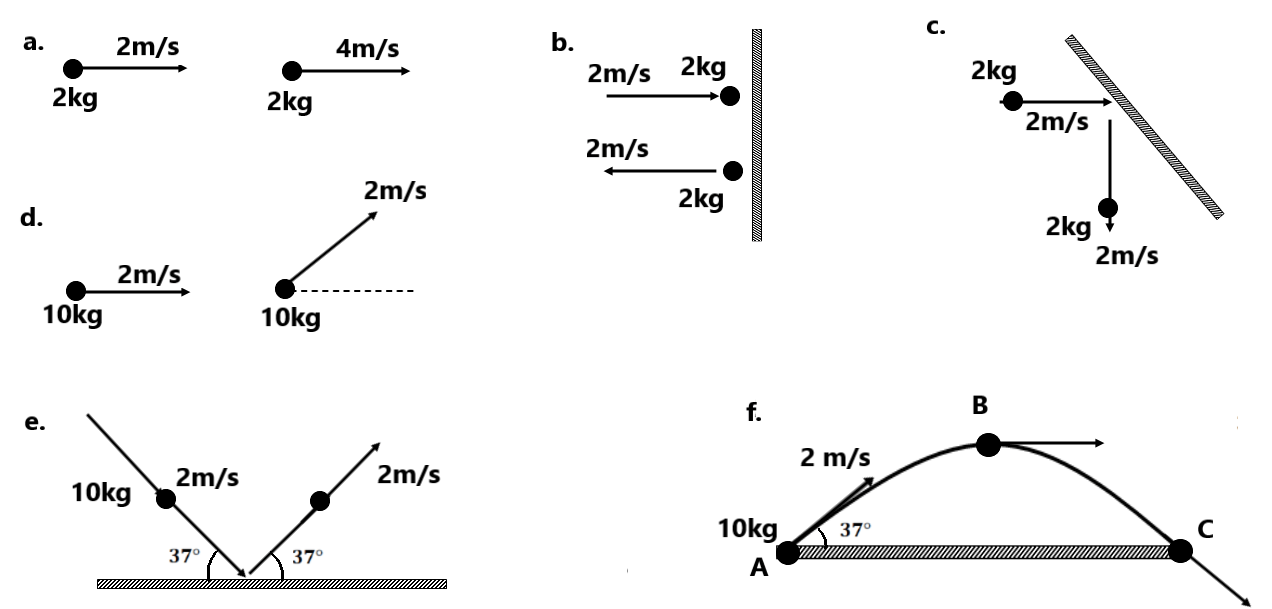
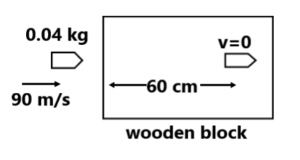
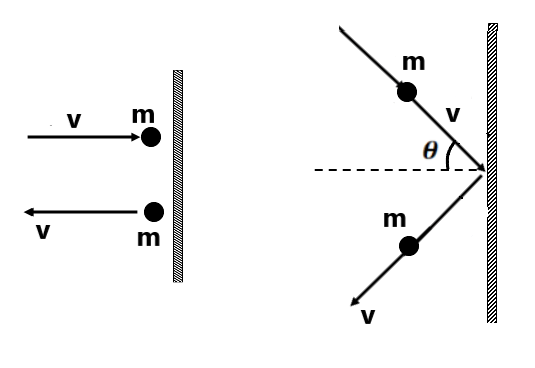
(3) The motion of a particle of mass m is described by (4) A constant force acts for 10 sec on a stationary body of mass 10kg. After which the force ceases to act. The body moves a distance of 50m with uniform speed in the next 5 sec. Find the magnitude of force. (10N) (5) A ship of mass (6) A 100 kg man jumps into a swimming pool from a height of 5m. It takes 0.4 sec for the water to reduce its velocity to zero. What is the average force exerted by the water on the man (g=10 m/s²) (2500N) (7) A girl pulls a box of mass 10.4 kg with a force of 25N inclined to the horizontal at an angle of 37°. As a result, the box accelerates horizontally. What is the magnitude of acceleration? (1.95 m/s²) (8) Sand drops vertically at the rate of 100 grams/sec on the horizontal belt conveyor moving at a steady velocity of 5 cm/sec. What is the force required to keep the belt moving? (9) A body of mass m=1kg falls from a height h=20m from the ground level. (a) What is the magnitude of the total change in momentum of the body before it strikes the ground? (10) An iron ball of mass m=50 gram falls from a height of h1=5m and rises up to h2=3.2m after colliding with the horizontal surface. If the time of contact of the iron ball is Δt=0.02 sec. Find the average force exerted on the ball by the horizontal surface. (45 j N) (11) Determine the magnitude and direction of force exerted by the ball on the wall in each case. Determine the direction of the force exerted by the wall on the ball in each case.
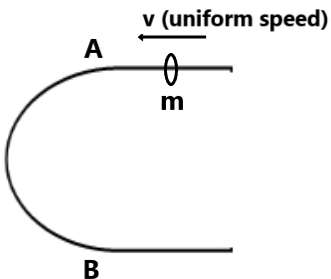
(12) Find the average force exerted by the beed on the circular part AB of the wire.(4mv²/πd)
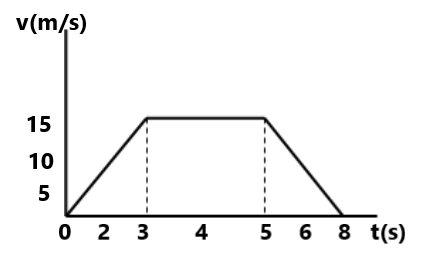
(13) A particle of mass 50 grams moves on a straight line. The (v-t) graph is given. Find the force acting on the particle at t=2 sec, 4 sec, and 6 sec.
(14) A body of mass 8kg is moved by a force F=3x N. where x is the distance covered. The initial position is x=2m and the final position is x=10m. If initially the body is at rest, find the final speed. (6 m/s) (15) If a bullet of mass 5 grams moving with a velocity of 100 m/s penetrates a wooden block up to 6cm. Find the average force imposed. (417 N) (16) Gravel is dropped on a conveyor belt at the rate of 0.5 kg/s. Find the extra force required to keep the belt moving at 2 m/s. (1N) (17) A body of mass 5kg starts from the origin with an initial velocity of |
NEWTON’S THIRD LAW
Force is always a two-body interaction. According to this law “To every action force, there is an equal and opposite reaction force “
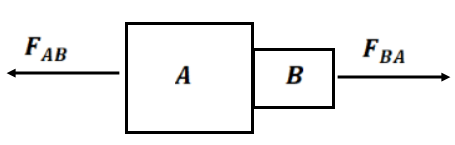
Action and reaction forces act on different bodies, not on the same body. Thus if we are considering the motion of any one body (A or B), only one of the forces is relevant. It is an error to add up the two forces and claim that the net force is zero.
In the case of two-particle systems having linear momentum are moving towards each other under mutual forces; from Newton’s 2nd law
Which is Newton’s 3rd law
FUNDAMENTAL FORCES IN NATURE
Actually, there are four fundamental forces that exist in nature.
(1) Gravitational Force:
(2) Electro-magnetic Force:
-
- Normal Force
- Tension Force
- Friction Force
- Spring Force
- Electrostatic Force
- Magnetic Force
(3) Strong Nuclear force: The nuclear force is the attractive force that holds the constituent particles of the atomic nucleus. This is the Strongest force in nature.
(4) Weak Nuclear Force: The weak nuclear force appears only in certain nuclear processes such as β decay of a nucleus. Weak nuclear force is much stronger than the gravitational force.
NORMAL FORCE
When one surface presses the other, normal force acts on both surfaces. It is a contact force that acts perpendicular to the surface in contact. (The horizontal component of contact force is frictional force between surfaces)
Draw the normal force on each body

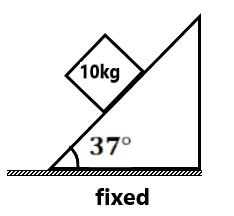
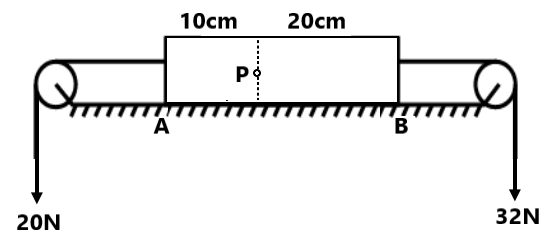
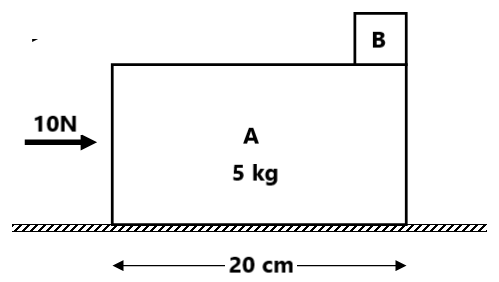
Exercise 3(1) find the normal force between (a) block and floor (b) Block and the wall ( 30N, 0)
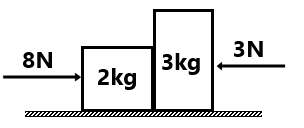
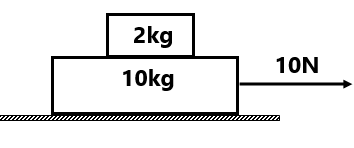
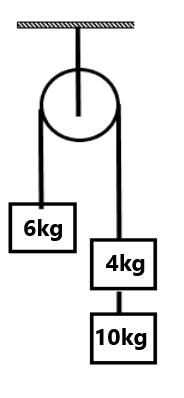
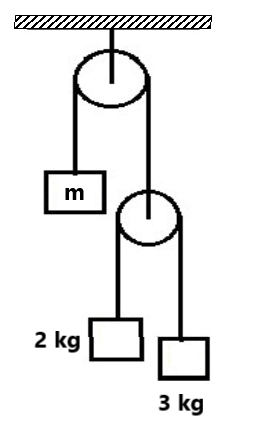
(2) Find the normal force between 2kg and 3 kg blocks. (6N)
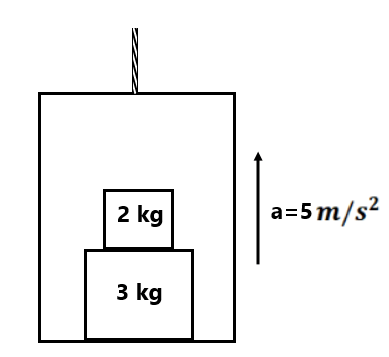
(3) Find the normal force between 2kg and 3 kg blocks and between 3kg and lift.
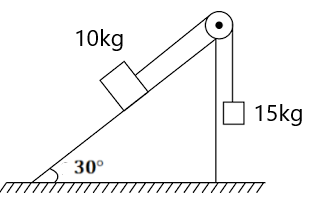
(4) Find the acceleration of the blocks and the normal force between the blocks. All surfaces are smooth. (4 m/s², 12N, 28N)
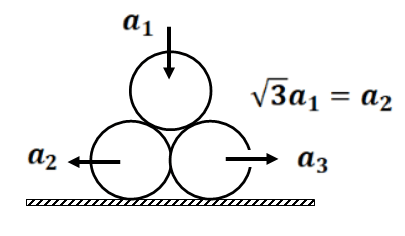
(5) Find the acceleration of smaller blocks as shown in Fig.
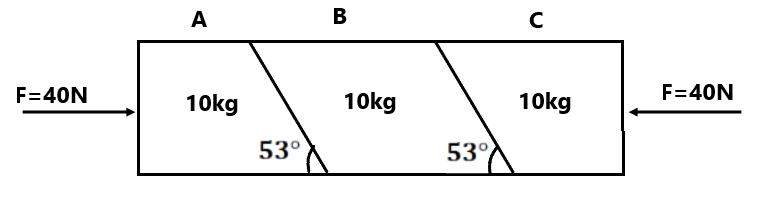
(6) Find the magnitude of normal reaction between blocks (A and B) and (B and C). Also find normal reaction applied by the ground on the blocks A, B, and C. ( 50N in all cases horizontal, 130N, 100N, 70N)
(7) Find the acceleration of both the blocks. ( 1m/s², 0)
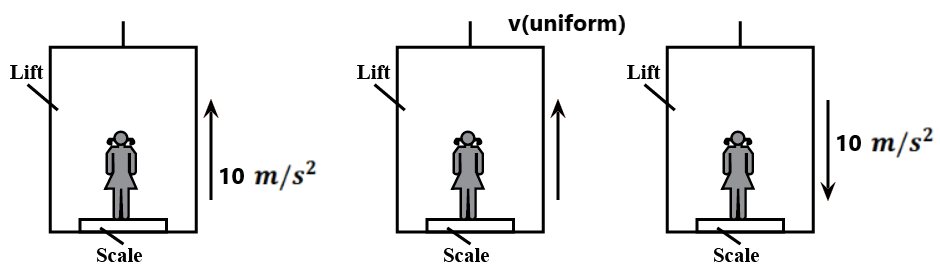
(8) What is the weight shown in a weighing machine of 60 kg man?
(9) What weight is shown in the weighing machine in different situations of 60 kg weight man?
|
TENSION FORCE
When the two ends of a string are pulled in opposite directions then a force develops in the string called tension.
Ideal string ( massless, smooth, in-extensible, circular)
- Tension at all points of the string will be the same.
- Tension in a string is always along the string and away from the object)
- The net force on an ideal string is always zero. (F=ma ⇒ F=0×a ⇒ F=0)
Draw the tension force on each string
Draw a Free Body Diagram (FBD) on each body as shown in fig
|
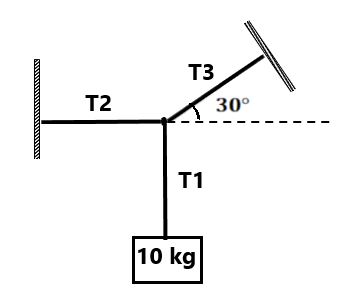
Exercise 4(1) The 10kg block is in equilibrium. Find the tension T1, T2, and T3. (100N, 100√3 N, 200N)
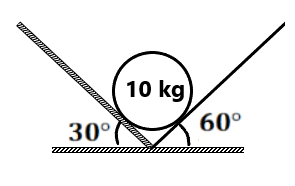
(2) Find the normal force by the walls on the sphere. ( 50N, 50√3 N)
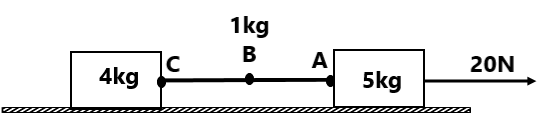
(3) Find the tension at points A,B, and C. The string is of uniform mass distribution and is of 1 kg. The blocks are kept on a horizontal frictionless surface. (10N, 9N, 8N)
(4) Find the value of T2. (30N)
(5) Find the acceleration of the blocks. (2.5 m/s²)
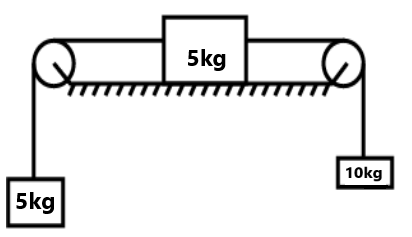
(6) Find the acceleration of blocks and tension on the string. (4 m/s², 60N, 84N)
(7) Find the acceleration of blocks and tension of the string. (4 m/s², 90N)
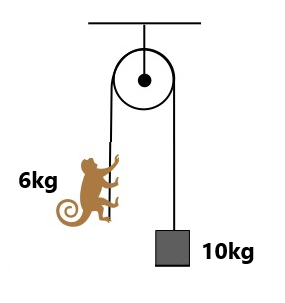
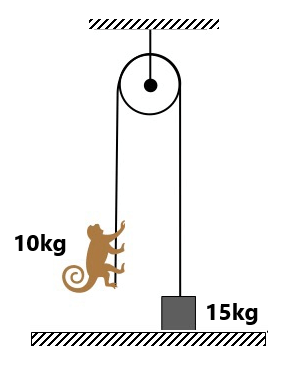
(8) A monkey of mass 5kg is climbing up a rope of breaking strength 150N, What is the maximum acceleration with which it can (g=9.8m/s²) (20 m/s²,10 m/s²) (a) Climb up the rope (9) A monkey of mass 6kg pulling the string downward with 120N force.
(a) What is the acceleration of monkey and block w.r.t ground? (10) What is the force exerted by the rope at point P. (164N)
(11) In order to raise the mass from the ground, the monkey must climb with (correct option a)
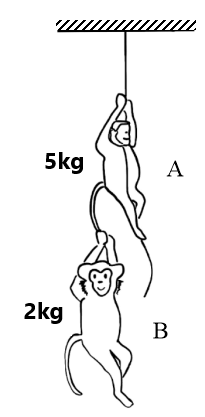
(a) Uniform acceleration greater than 5m/s² (12) If A can tolerate a tension of 30N in its tail, what force should it apply on the rope in order to carry monkey B with it? (g=10m/s²) (between 70N to 105N)
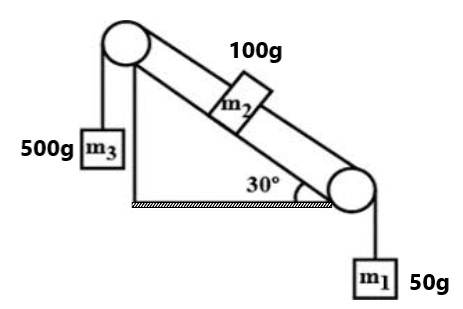
(13) Find the acceleration of the system in both cases (8g/13 m/s², g/10 m/s²)
(14) Find the force at point P. Mass of rod=3 kg (uniformly distributed) (24N)
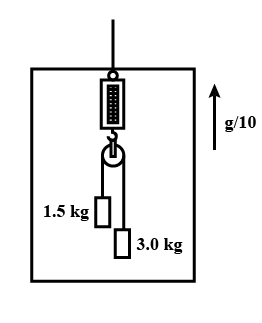
(15) An empty plastic box of mass m is found to accelerate up at the rate of g/6 when placed deep inside water. How much sand should be put inside the box so that it may accelerate down at the same rate g/6? (2m/5) (16) Find the reading of the spring balance shown in Fig (4.4 kg)
(17) Find the tension in the string if the elevator
(a) Goes up with an acceleration of 1.2 m/s². (0.55 N) (18) Calculate the mass of the man as registered by a weighing machine. (mcosθ)
|
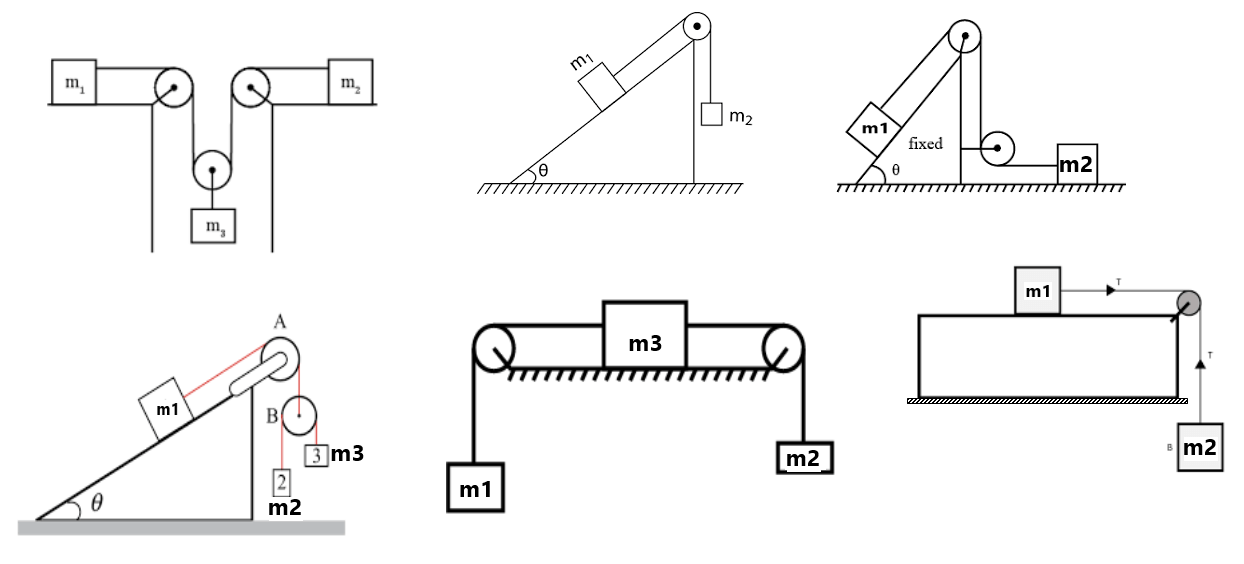
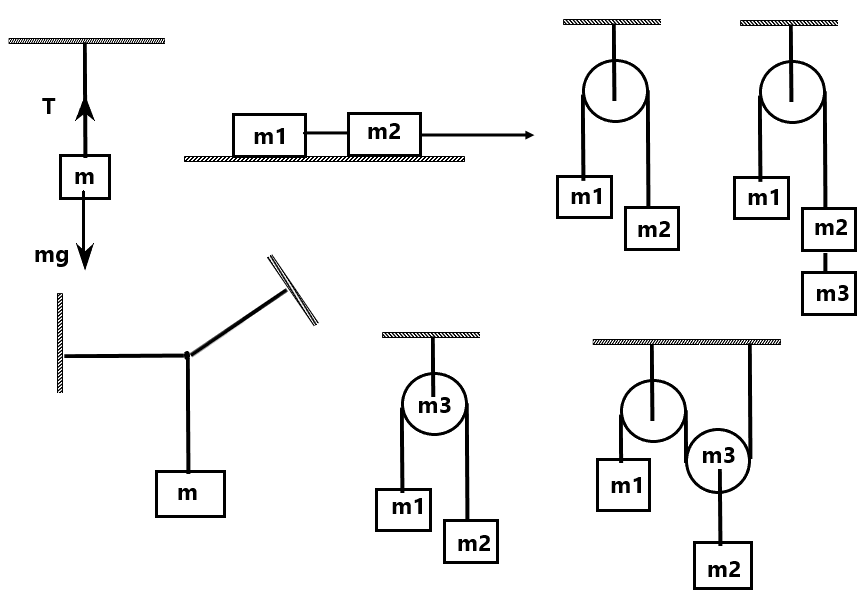
Constraint Motion
When two or more objects are connected to each other such that the motion of one affects the path and motion of the other, this is called constrained motion. The relation between velocity/ acceleration due to constraint is called constraint is called constraint equation.
String Constraints
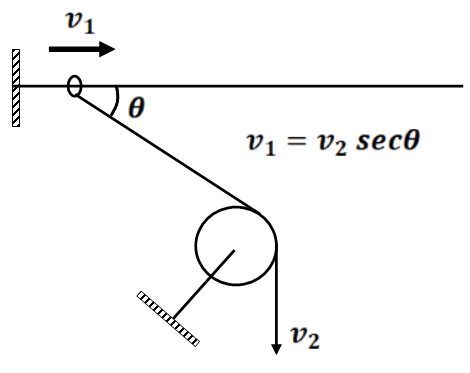
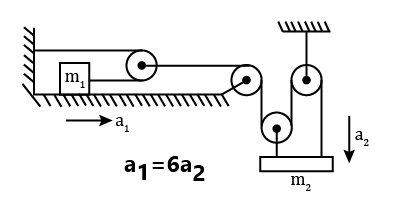
- If two or more blocks are connected by an in-extensible string directly or indirectly, we can use the constraint that length remains constant i.e.
is the length of the string.
- If two ends of an in-extensible string are moving with different velocities, the component of velocity along the length of the string must be the same for the string to be taut.
- Shortcut trick “The sum of dot product of tension and acceleration/ velocity of all messes should be zero.” i.e.
- In the case, where the pulley moves along with the blocks connected on both sides, we can say that the displacement of the pulley is the average of the displacement on both sides of the pulley.
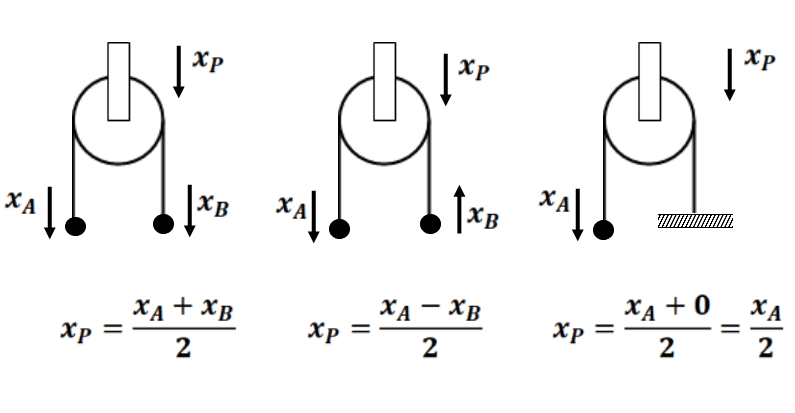
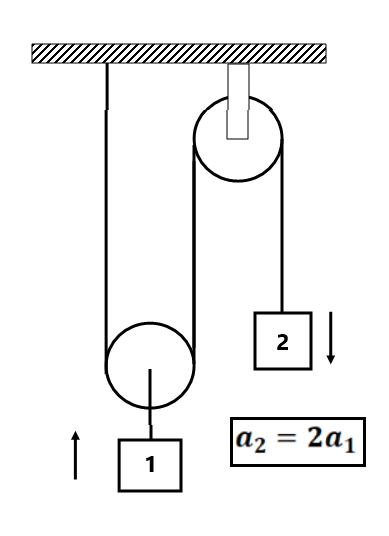
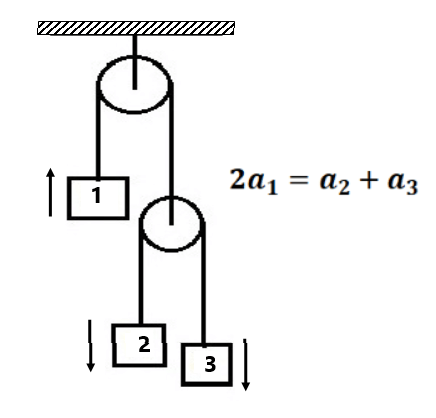
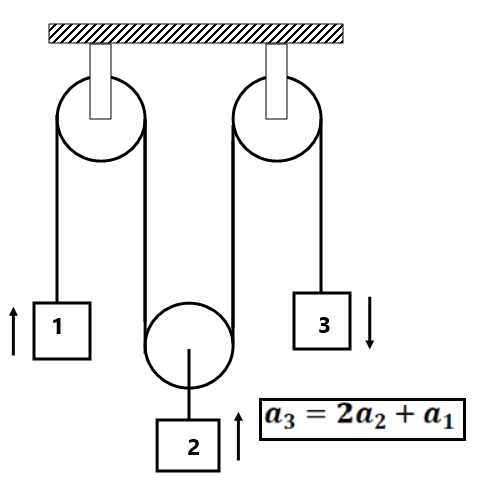
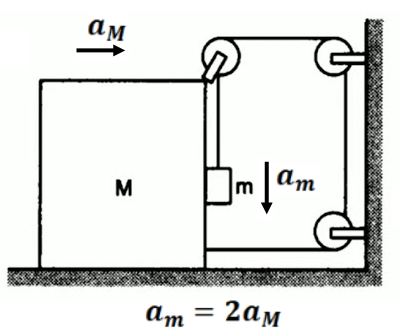
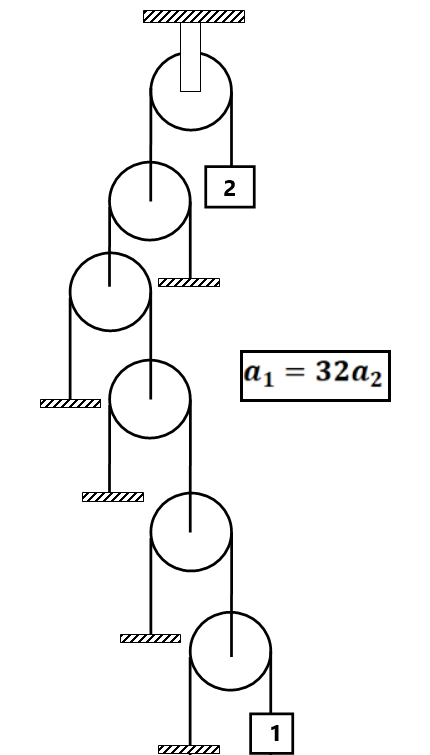
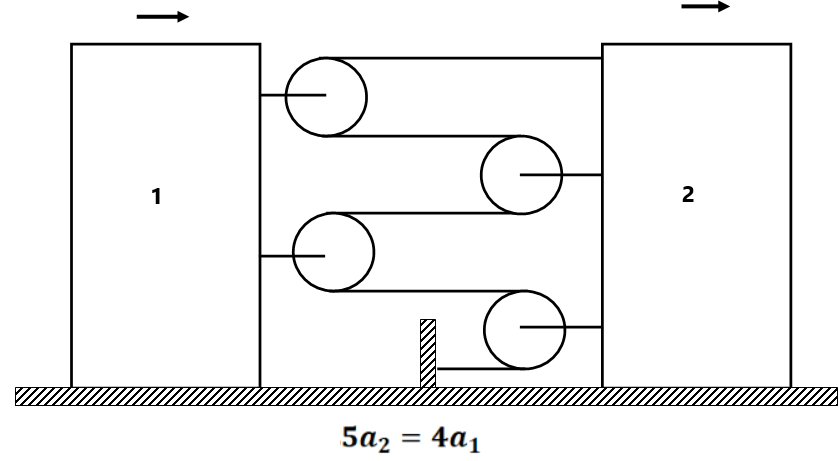
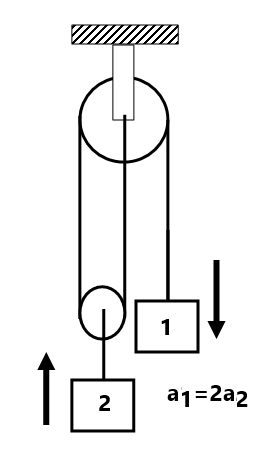
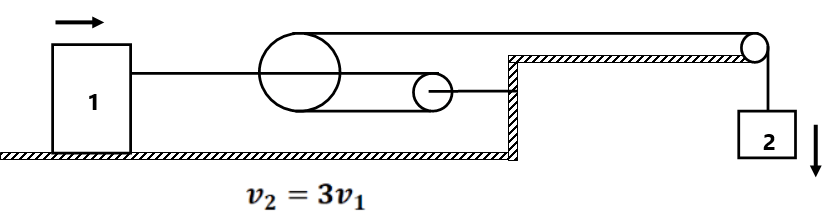
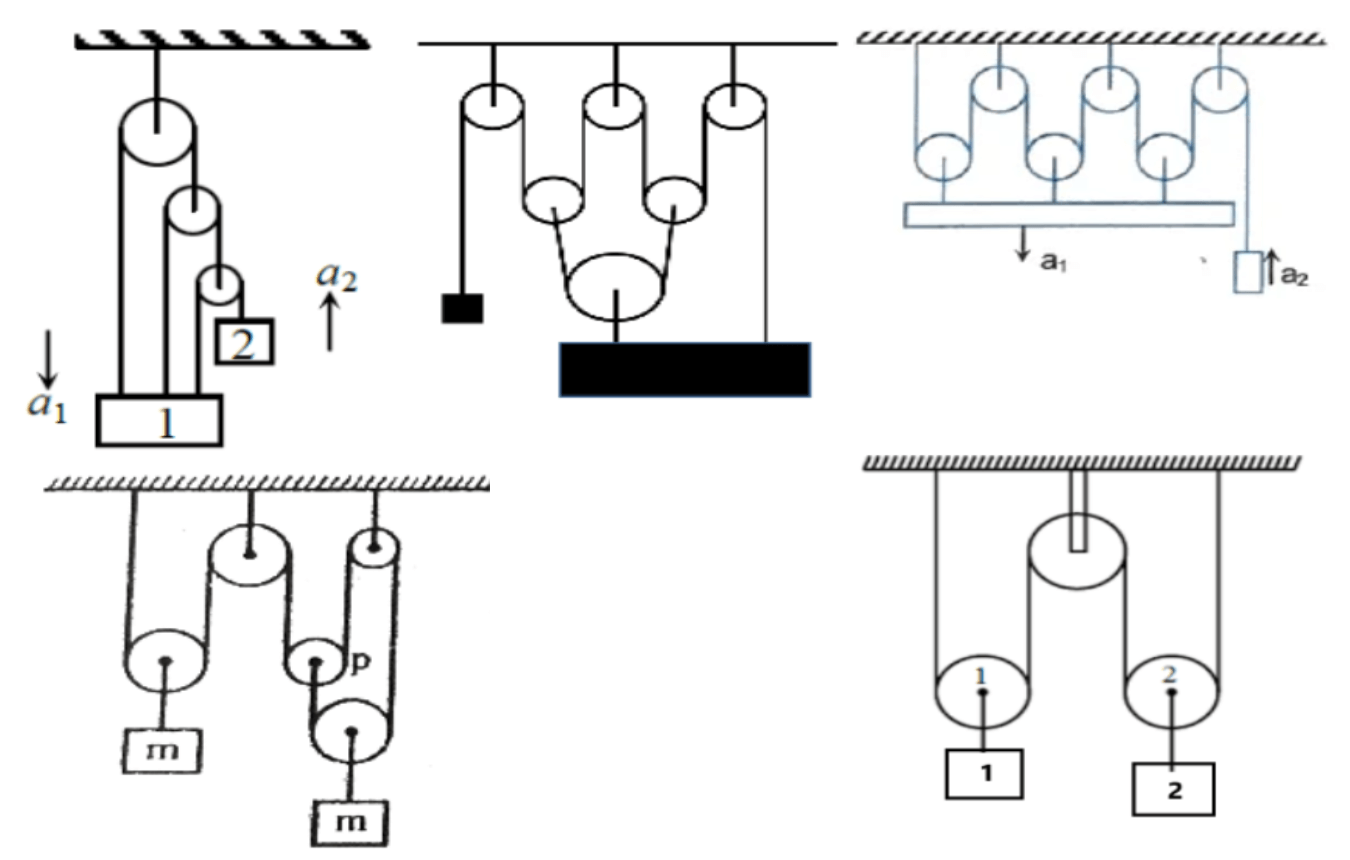
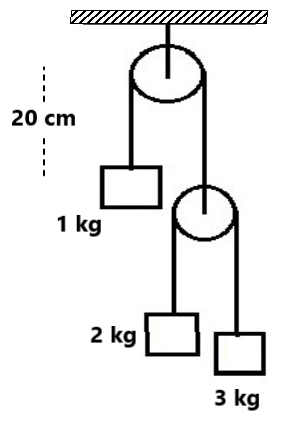
Find the constraint relation between the blocks as shown in fig
|
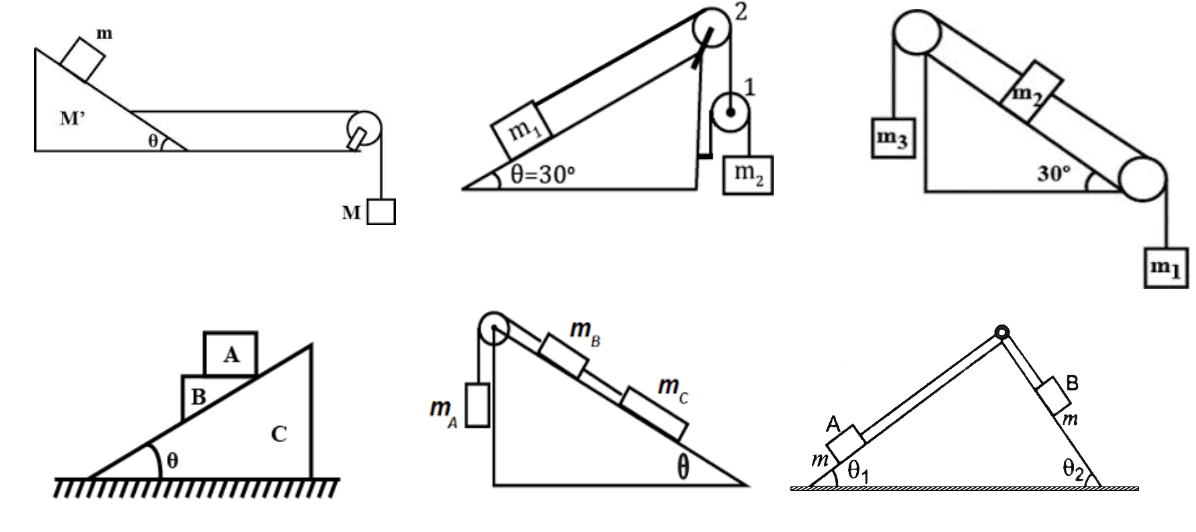
Normal Constraints
If two objects are moving such that they are in contact, then the component of velocity/ acceleration along the normal at the contact point must be equal. (acceleration should be taken w.r.t ground)
Combination of wedge and pulley constraints
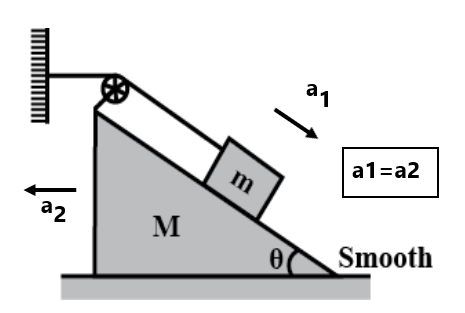
Rigid body constraints
For a rigid body, the component of velocity along the line joining any two points must be the same.
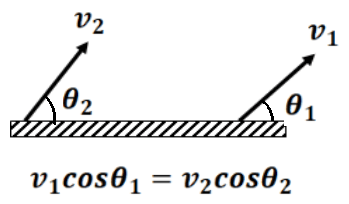
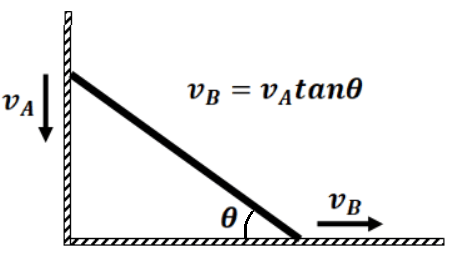
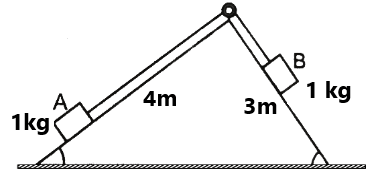
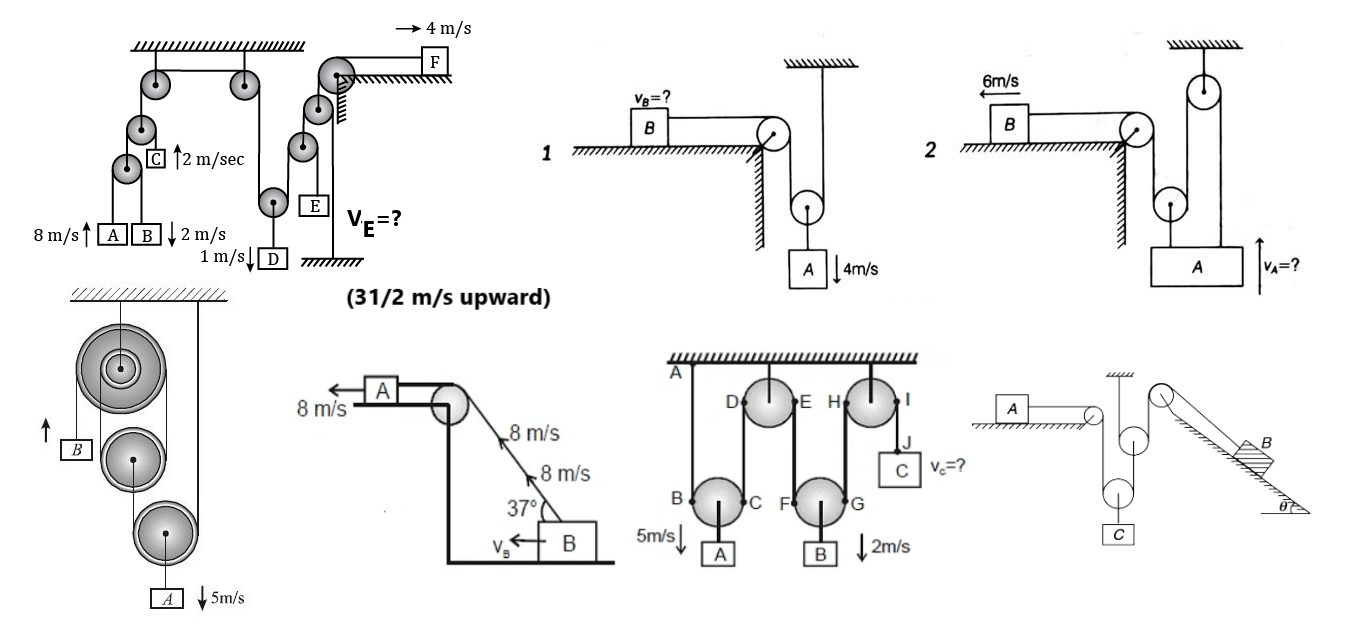
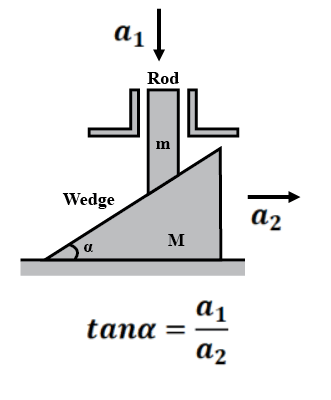
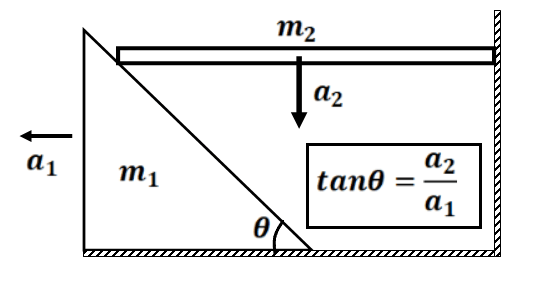
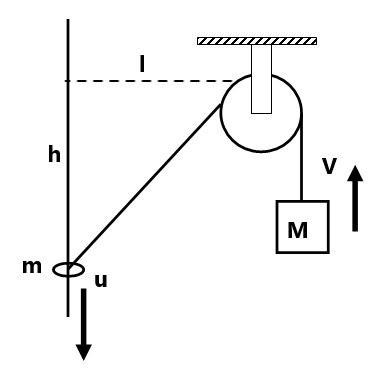
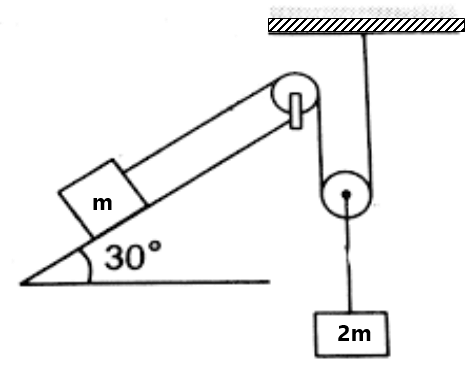
Exercise 5(1) Find the constraint relation between the blocks as shown in fig:
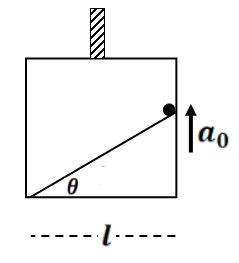
(2) Acceleration of the block A is
(3) if
(4) What will be the acceleration of the block as observed from the ground?
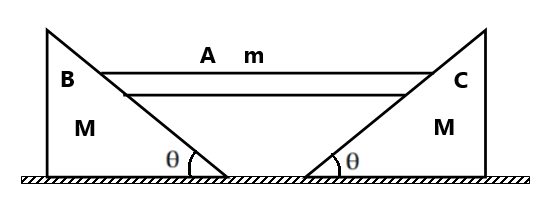
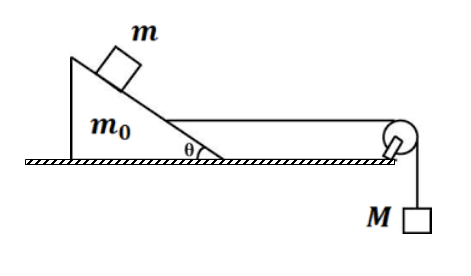
(5) A plank of mass m rests symmetrically on two wedges B and C of mass M. What is the acceleration of the plank? Neglect friction between all the contact surfaces.
|
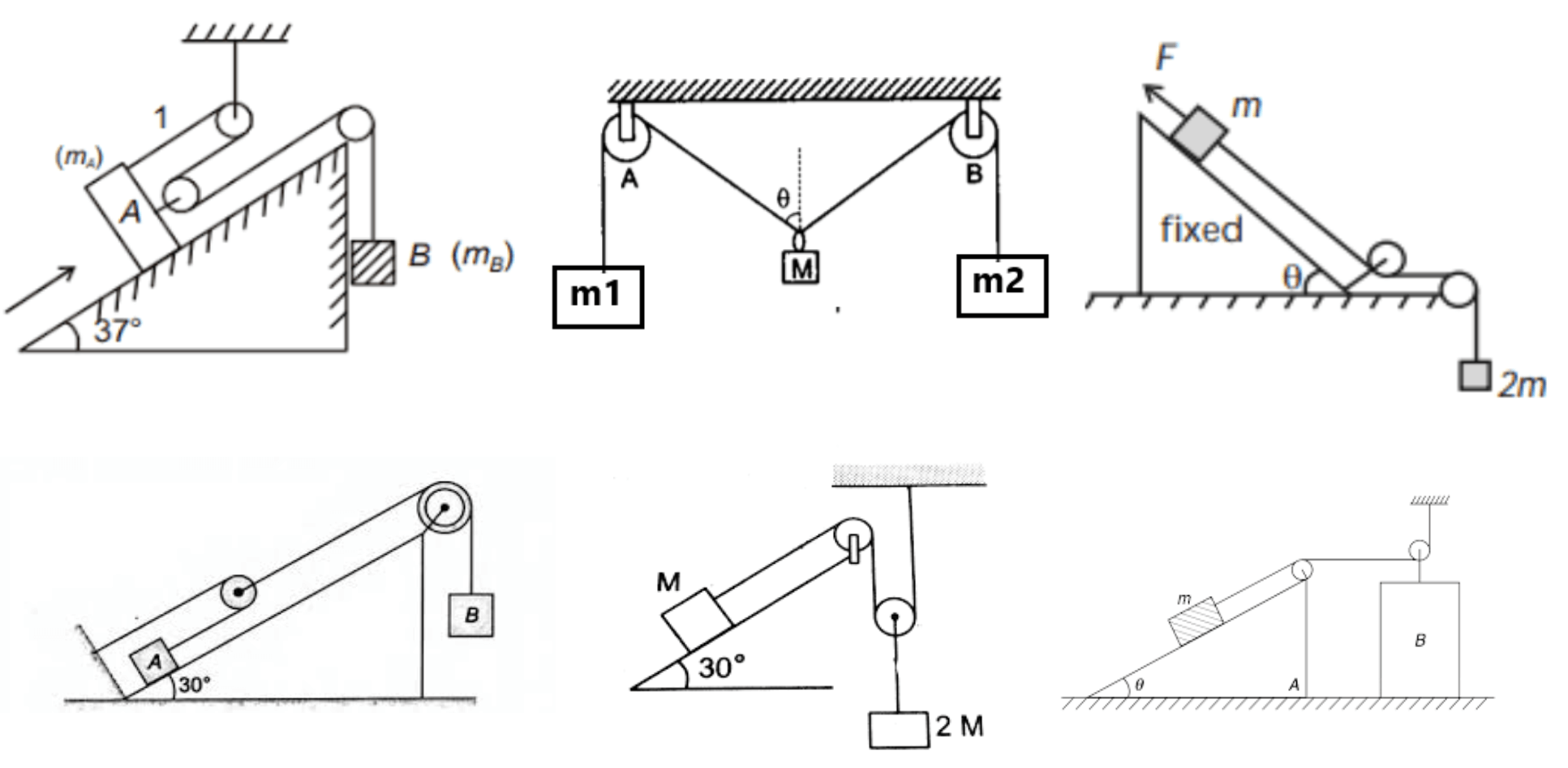
Frame of Reference (Concept of Pseudo force)
There are two types of Frame of reference
- Inertial Frame ( a=0)
- Which is either at rest or moving with uniform velocity
- Newton’s 2nd law is applicable to this frame
- Non-Inertial Frame (a≠ 0)
- Which are accelerating
- Newton’s 2nd law is not applicable from this frame
When the observer is in a non-inertial frame, then to apply Newton’s law we have to apply an imaginary force known as pseudo force.
It arises due to relative acceleration and not due to any interaction (i.e. has no action and reaction pair)
Its magnitude is the product of the mass of the body and the acceleration of the non-inertial frame, and its direction is just opposite to the acceleration of the non-inertial frame.
Let us try to understand from a simple Example
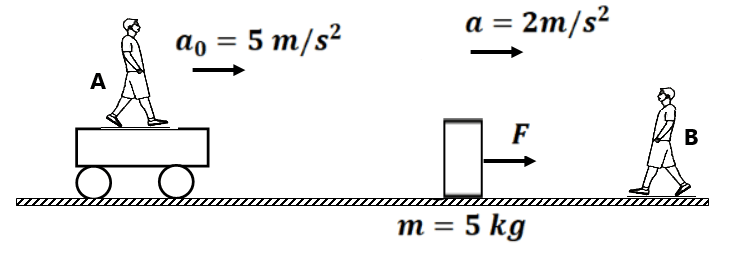
For B (Intertial Frame)
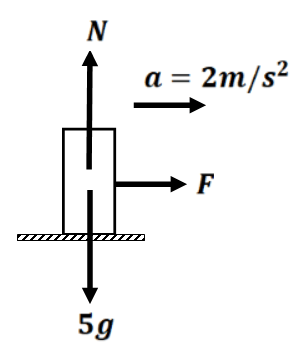
a=2 m/s² is the acceleration of mass m=5kg w.r.t observer B
Now,
For A ( Non-Inertial Frame)
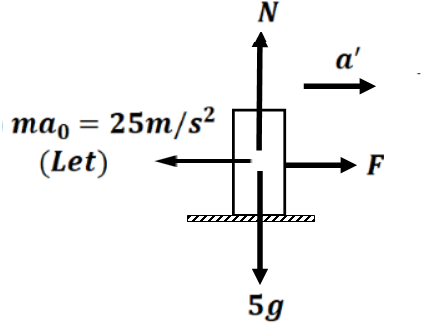
is the acceleration of Frame w.r.t B (ground) and
is the acceleration of mass m= 5kg w.r.t. A
Now,
from relative motion, we can write
which is the same as the previous
If we want to apply Newton’s second law on an object from an inertial frame, then an imaginary force ( here ) will have to be applied in the opposite direction of the frame. This force is known as pseudo force.
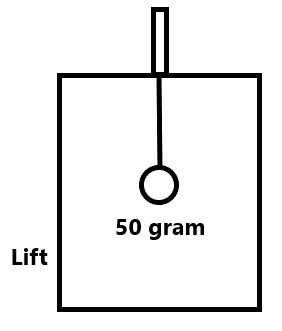
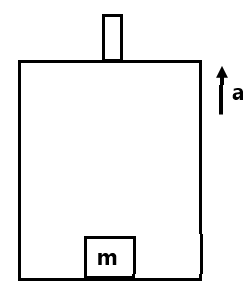
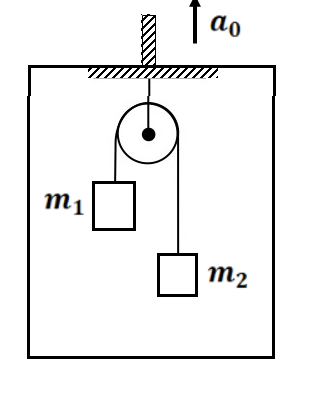
Exercise 6(1) Find the normal force on the block by the lift. ( mg+ma)
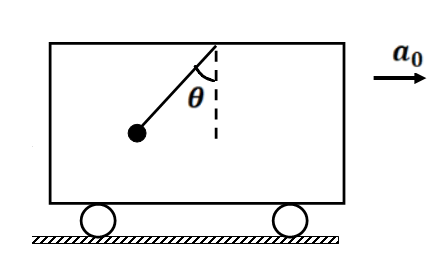
(2) Find the angle made by the string with the vertical at equilibrium.
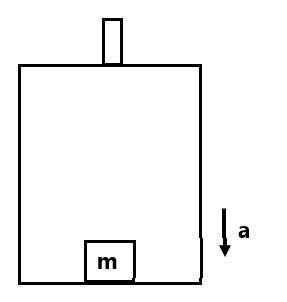
(3) With what acceleration ‘a’ should the box descend so that the block of mass m exerts a force mg/4 on the floor of the box?
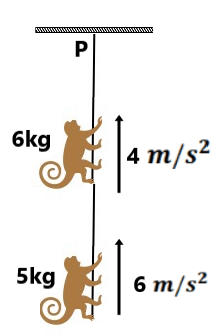
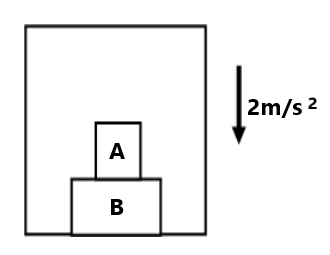
(4) the mass of A is 0.5 kg. What force is exerted by block A on the block B? ( 4N)
(5) Find the time elapsed before the block separated from A. ( 0.45 sec)
(6) What should be the mass m so that it remains at rest? (4.8 kg)
(7) Find the acceleration of the block
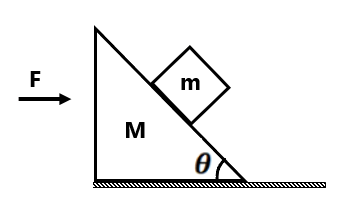
(8) For what value of F will the block of mass m remains at rest with respect to the wedge? All surfaces are frictionless.
(9) The system is released from rest. How long will it take before a 1 kg block strikes the pully?
(10) Find the acceleration of the block m. (g/3)
(11) Find the mass M ( hanging block) which will prevent the smaller block from slipping over the wedge.
(12) Find the time taken by the particle to reach the bottom.
(13) Find the time by the particle to reach the bottom.
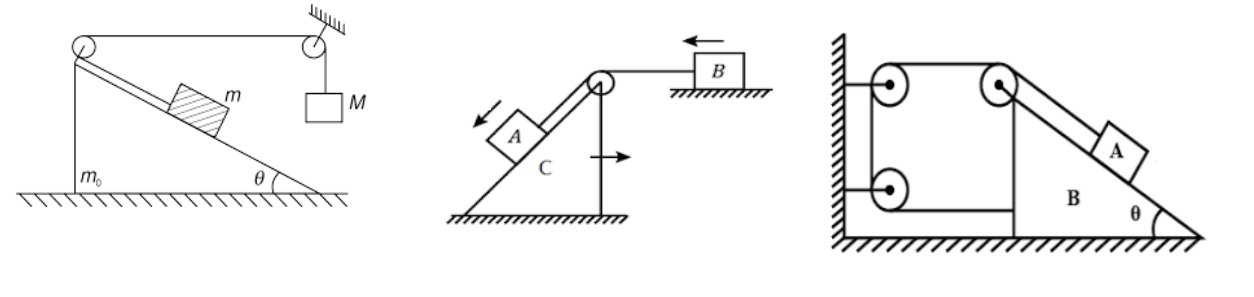
(14) Find the acceleration of the ब्लॉक्स।
(15) Find the magnitude and direction of acceleration of the body. ( 2 m/s², 37°)
(16) A body of mass 0.4 kg moving initially with a constant speed of 10 m/s to the north is subjected to a constant force of 8N directed towards the south for 30 sec. take the instant the force is applied is to t=0, the position of the body at that time to be x=0. Predict its position at t= -5 sec, 25 sec, and 100 sec. ( 50 m, 6 km, 50 m) (17) A truck starts from rest and accelerates uniformly at 2m/s². At t=10 sec, a stone is dropped by a person standing on the top of the truck ( 6 m high from the ground) What are the (a) velocity and (b) acceleration of the stone at t= 11 sec? ( 22.4 m/s, tanθ=10/20, 10 m/s²) |
Exercise 7(1) If a ball is thrown up in a moving train, it comes back to the person’s hands. Why? (2) A passenger sitting in a carriage at rest pushes it from within. Will the carriage move? (3) A stone when thrown on a glass window smashes the windowpane to pieces, but a bullet from the gun passes through making a clean hole. Why? (4) Why do bodies of small mass require a small initial effort to bring them into motion? (5) Why do the blades of an electric fan continue to rotate for some time after the current is switched off? (6) Why are passengers thrown forward from their seats when a speeding bus stops suddenly? (7) Can a body in linear motion be in equilibrium? (8) A body is acted upon by a number of external forces. Can it remain at rest? (9) If the net force acting on the body is zero, will the body remain necessarily in rest position? explain. (10) Why does an athlete run some steps before taking a jump? (11) An astronaut accidentally gets thrown out of his small spaceship accelerating in inter-stellar space at a constant rate of 100 m/s². What is the acceleration of the astronaut the instant after he is outside the spaceship? (12) Why is Newton’s first law of motion also called the Law of inertia? (13) A thief jumps from the upper storey of a house with a load on his back. What is the force of the load on his back when the thief is in the air? (14) A soda water bottle is falling freely. Will the bubbles of the gas rise in the water of the bottle? (15) A bird is sitting on the floor of a wire cage and the cage is in the hand of a boy. The bird starts flying in the cage. Will the body experience any change in the weight of the cage? (16) Why are shockers used in cars? (17) According to Newton’s third law, every force is accompanied by equal and opposite force. How can anything move then? (18) The distance travelled by a body is directly proportional to time. Is any external force acting on it? (19) Chinawares are wrapped in straw paper before packing. Why? (20) Why is it difficult to drive a nail into a wooden block without supporting it? (21) Two bodies of mass M and m are allowed to fall from the same height. If the air resistance be same for each body, will the two bodies reach the Earth simultaneously? (22) There is some water in a beaker placed on the pan of a spring balance. If we dip our finger in this water without touching the bottom of the beaker, then what would be the effect on the reading of the balance? (23) When a body falls to the earth, the earth also moves up to meet it. But the earth’s motion is not noticeable. Why? (24) Three forces F1, F2, and F3 are acting on a particle of mass m, such that F2 and F3 are mutually perpendicular, and under their effect, the particle remains stationary. What will be the acceleration of the particle, if the force F1 is removed? (25) A long rope is hanging, and passes over a pulley. Two monkeys of equal weight climb up from the opposite ends of the rope. One of them climbs up more rapidly relative to the rope. Which monkey will reach first at the top? The pulley is frictionless and the rope is massless and inextensible. (26) Can a single isolated force exist in nature? Give reason. (27) A block of mass M is supported by cord C from a rigid support, and another cord D is attached to the bottom of the block. If you give a sudden jerk to D, it will break. But if you pull on D steadily, cord C will break. Why?
(28) Newton’s 2nd law is the real law of motion. Explain? |
Exercise 8Fill in the blank (1) The cause of every accelerated motion is an ________ force. (2) Newton’s first law of motion is also called the law of _______. (3) A force of kg wt contains ______ newtons. (4) Newton’s second law of motion gives the measurement of _______. (5) The velocities of bodies having equal linear momentum are _______ proportional to their masses. (6) _______ of a body is the measure of its inertia. (7) A body of mass m moves along the x-axis such that its position coordinates at any instant t is (8) A gravitational unit is _____ times the corresponding absolute unit. (9) One Newton is that force that produces an acceleration of _______ in a body of mass ______. True and false (1) No force is required to move a body with uniform velocity. (2) A body in linear motion can be in equilibrium. (3) A force acts always in the direction of motion. (4) If the net force acting on a body is zero, the body will remain necessarily at rest position. (5) Action and reaction forces are equal and opposite. They cannot cancel each other. (6) Two similar trains are moving along the equatorial line with the same speed but in opposite directions. They will exert equal pressure on the rail. |