प्रिज्म (Prism)
किसी कोण पर झुके दो समतल पृष्ठों के बीच घिरे समांगी , पारदर्शी माध्यम को प्रिज्म कहते है ।
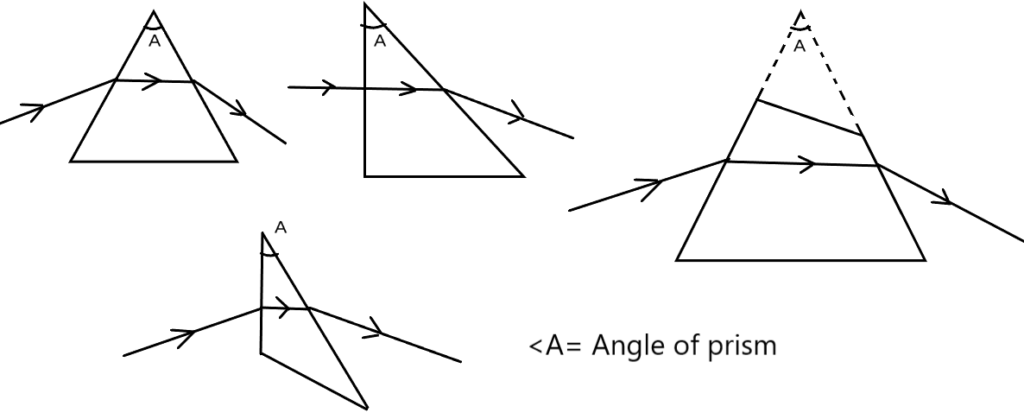
प्रिज्म से सम्बंधित कुछ मत्वपूर्ण शब्द
- प्रिज्म कोण :- दोनों अपवर्तक पृष्ठों के मध्य कोण प्रिज्म कोण या अपवर्तन कोण कहलाता है , इसे A से निरूपित किया जाता है ।
- आपतन कोण :- यह वह कोण है जो आपतित किरण उस तल के अभिलम्ब के साथ बनाती है , जिस सतह से किरण पहली बार प्रिज्म से टकराती है ।
- निर्गत कोण :- यह वह कोण है जो प्रिज्म से निकलने वाली किरण ( निर्गत किरण ) उस तल के अभिलम्ब के साथ बनाती है , जिस सतह के किरण प्रिज्म से बहार निकलती है ।
- विचलन कोण :- प्रिज्म को पार करने के बाद आपतित किरण जितने कोण से मुड़ जाती है उसे विचलन कोण कहते है । दूसरे शब्दों में हम यह कह सकते है की विचलन कोण ,आपतित किरण तथा निर्गत किरण के बीच के कोण है । इसे (
) द्वारा सूचित किया जाता है ।
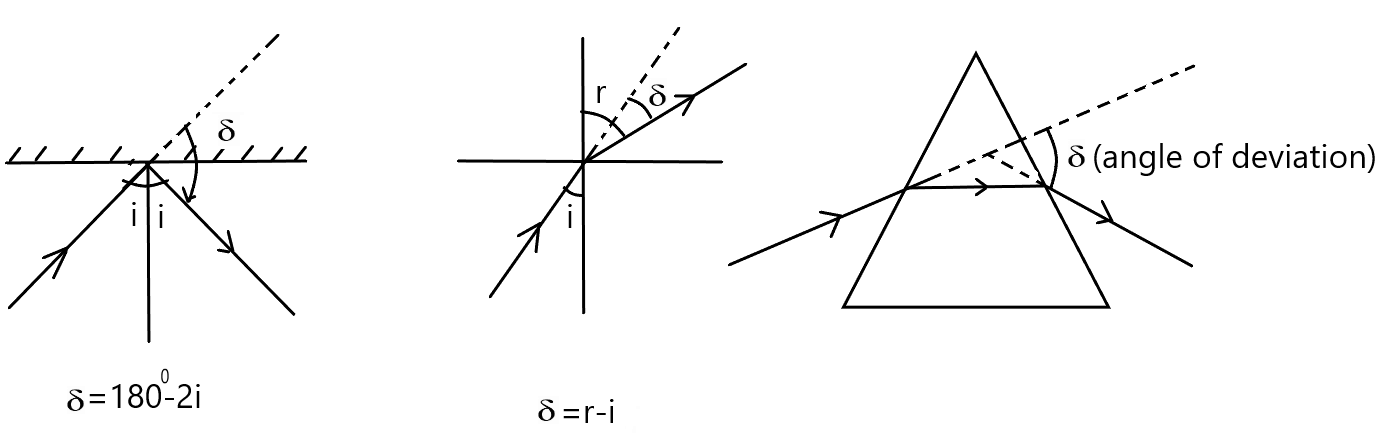
प्रिज्म से अपवर्तन
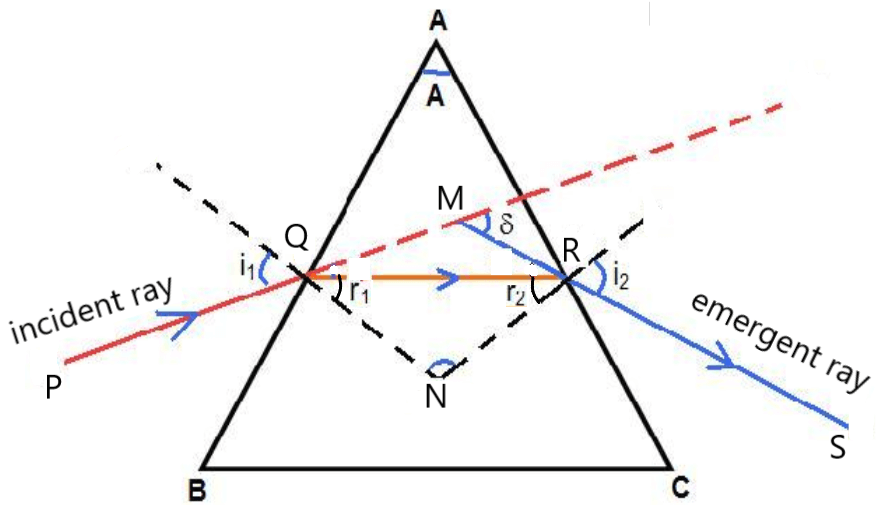
माना की ABC एक प्रिज्म है जिसका अपवर्तन या प्रिज्म कोण A है । एक किरण PQ जो प्रिज्म के AB सतह पर कोण के साथ आपतित होती है . अपवर्तन के बाद यह किरण लम्ब की ओर मुड़ जाती है तथा AB के साथ अपवर्तन कोण
बनाती है । अपवर्तित किरण QR सतह AC पर
कोण के साथ आपतित होती है तथा निर्गत कोण
के साथ बाहर निकल जाती है ।
चित्र के अनुसार , विचलन कोण है
चतुर्भुज AQNR से
समीकरण (a) तथा (b) से
समीकरण (1) से
यहाँ से हमें यह पता चलता है की विचलन कोण , आपतन कोण तथा प्रिज्म कोण पर निर्भर करता है ।
माना की प्रिज्म के पदार्थ का अपवर्तनांक है ।
पहले सतह AB में , स्नेल के नियम के अनुसार
छोटे कोण के लिए
उसी प्रकार स्नेल का नियम AC सतह के लिए
हम जानते है की
NOTE:- यह सूत्र तभी मान्य होगा , जब अपवर्तन या प्रिज्म कोण का मान बहुत ही छोटा हो ।
प्रिज्म सूत्र
हम जानते है की प्रिज्म का विचलन कोण , आपतन कोण के साथ इस प्रकार निर्भर करता है
इस सूत्र से यह पता चलता है की के एक मान के लिए दो आपतन कोण
तथा
होंगे । क्योंकि हम जानते है की प्रकाश के विभिन्न माध्यमों में चलने के मार्ग में यदि किसी बिन्दु पर उसकी दिशा पलट दी जाए तब उसके चलने के मार्ग में उत्क्रमणीय व्यवहार दिखाई देता है।
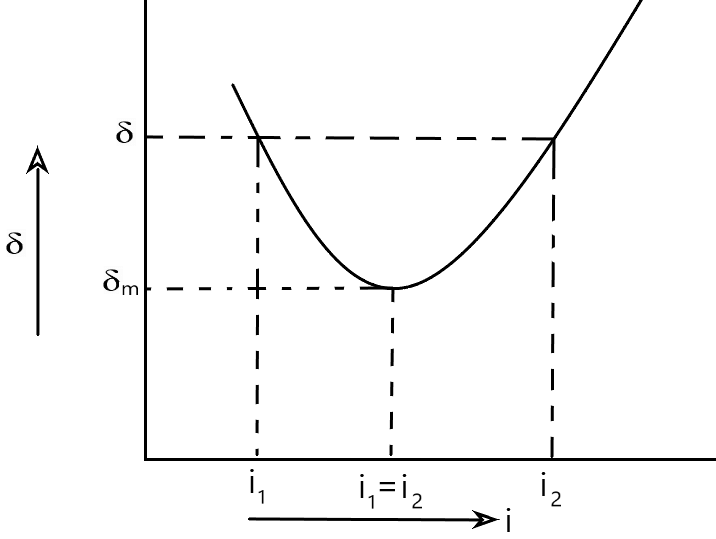
उपर्युक्त ग्राफ से हम देखते है की , आपतन कोण के साथ साथ विचलन कोण का मान घटता जाता है । आपतन कोण के एक विशेष मान के लिए विचलन कोण का मान न्यूनतम () हो जाता है , यह स्थिति न्यूनतम विचलन की स्थिति कहलाती है । आपतन कोण को और अधिक बढ़ाने पर विचलन कोण भी बढ़ने लगता है । इस प्रकार एक और केवल एक ही विशेष आपतन कोण के लिए प्रिज्म न्यूनतम विचलन उत्पन्न करता है ।
न्यूनतम विचलन की स्थिति में =
तथा
हम जानते है की
उसी प्रकार
स्नेल का नियम AB सतह के लिए
यह प्रिज्म सूत्र है । इसका उपयोग साधारणतः प्रिज्म के पदार्थ का अपवर्तनांक निकालने के लिए किया जाता है ।
NOTE:
महत्तम विचलन के लिए आपतन कोण का मान महत्तम होना चाहिए । अर्थात
किस स्थिति में प्रकाश की किरण प्रिज्म से बाहर नहीं निकल पाएगी ।( OUT OF SYLLABUS)
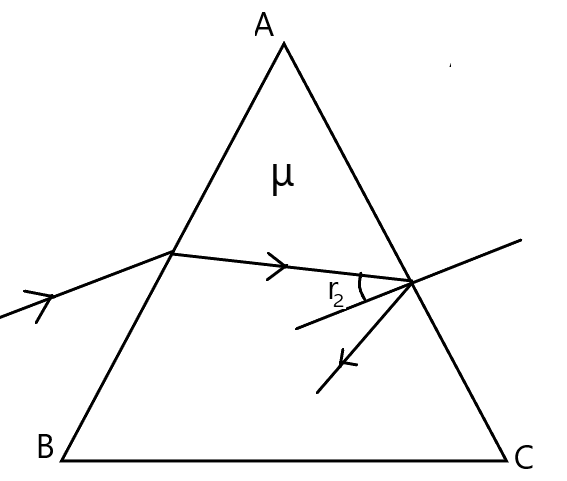
चित्र के अनुसार यदि सतह AC पर प्रकाश का पूर्ण आतंरिक परावर्तन होता है , तब प्रकाश प्रिज्म से बाहर न जाकर पुनः वापस लौट आती है ।
तभी महत्तम होगा जब
महत्तम होगा , और हम जानते है की
का महत्तम मान 90° होता है
from (1)
पूर्ण आतंरिक परावर्तन के लिए
अतः यदि [ ] तब किसी भी आपतन कोण के लिए प्रकाश की किरण प्रिज्म से बाहर नहीं जा पाएगी
अर्थात , यदि प्रिज्म कोण , उसके क्रांतिक कोण के दोगुने से अधिक होगा तो कोई भी किरण प्रिज्म से बाहर नहीं निकल पाएगी ।
अभ्यासार्थ प्रश्न(1) एक समबाहु प्रिज्म के पदार्थ का अपवर्तनांक √3 है । इससे उत्पन्न न्यूनतम विचलन कितना होगा । (60°) (2) एक प्रिज्म का कोण 30° है । इसकी एक अपवर्तक सतह पर 60° के कोण से आपतित प्रकाश किरणों का 30° विचलन होता है तो निर्गत कोण की गणना करें ।( 0°) (3) एक पतले प्रिज्म के पदार्थ का अपवर्तनांक 1.65 है । यह एक प्रकाश किरण को 7.5° पर विचलित कर देता है । प्रिज्म का कोण ज्ञात कीजिये । ( 11.54°) (4) एक प्रिज्म के पदार्थ का अपवर्तनांक √2 है तथा अपवर्तक कोण 60° है । न्यूनतम विचलन के लिए आपतन कोण का मान कितना होना चाहिए । (45°) (5) जब प्रकाश के एक पुंज को प्रिज्म से गुजारा जाता है तो न्यूनतम विचलन 40° होता है । यदि प्रिज्म कोण का मान 60° है तो प्रिज्म के पदार्थ का अपवर्तनांक कितना होगा । (1.532) (6) 60° कोण वाले एक प्रिज्म के पदार्थ का अपवर्तनांक √2 है । न्यूनतम विचलन की स्थिति में ज्ञात कीजिये (a) न्यूनतम विचलन कोण (b) आपतन कोण (c) अपवर्तन कोण (d) निर्गत कोण (30°, 45°, 30°,45°) (7) काँच के पतले प्रिज्म में न्यूनतम विचलन कोण (8) यदि काँच के एक पतले प्रिज्म को जल में डुबो दिया जाये तो सिद्ध कीजिये की प्रिज्म द्वारा प्रकाश किरण न्यूनतम विचलन एक चौथाई रह जायेगा । (9) एक प्रिज्म का अपवर्तन कोण 30° तथा उसके पदार्थ का अपवर्तनांक √2 है । प्रिज्म के दूसरे अपवर्तक पृष्ठ पर चांदी की कलई कर दी गई है । आपतन कोण का मान कितना होना चाहिए की प्रकाश पुनः उसी माध्यम में वापस लौट आये । ( 45°) (10) 60° कोण के प्रिज्म द्वारा उत्पन्न न्यूनतम विचलन कोण 30° है । यदि निर्वात में प्रकाश का वेग |
प्रिज्म द्वारा वर्ण विक्षेपण ( Dispersion by a Prism)
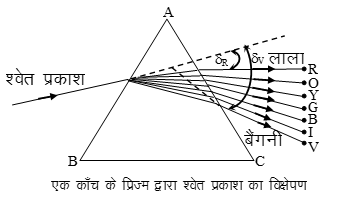
जब प्रकाश काँच के किसी प्रिज्म से गुजरता है तो वह अपने अवयवी रंगों में विभक्त हो जाता है । यह घटना प्रकाश का वर्ण विक्षेपण कहलाती है । तथा प्राप्त रंगों की पट्टी को स्पेक्ट्रम या वर्णक्रम कहते है । श्वेत प्रकाश के वर्णक्रम में सात रंग विद्यमान होते है । ये रंग क्रमशः लाल , नारंगी , पीला , हरा , आसमानी , नीला तथा बैगनी होते है । बैगनी रंग का विचलन सबसे अधिक तथा लाल रंग का विचलन सबसे कम होता है ।
प्रश्न :- क्या प्रिज्म स्वयं किसी तरह से रंग बनाता है या यह केवल सफेद प्रकाश में पहले से मौजूद रंगों को अलग करता है?
उत्तर :- प्रिज्म द्वारा वर्ण विक्षेपण की घटना में जब श्वेत प्रकाश से सात रंग निकलती है तो ठीक उस प्रिज्म के सामने उसी जैसा एक प्रिज्म उलटकर रख दिया जाता है जैसा की चित्र में दिखाया गया है । जिससे ,पहले प्रिज्म का सभी रंग के प्रकाश दूसरे प्रिज्म में आपतित होती है । हम देखते है की दूसरे प्रिज्म से पुनः श्वेत प्रकाश ही निर्गत होता है ।
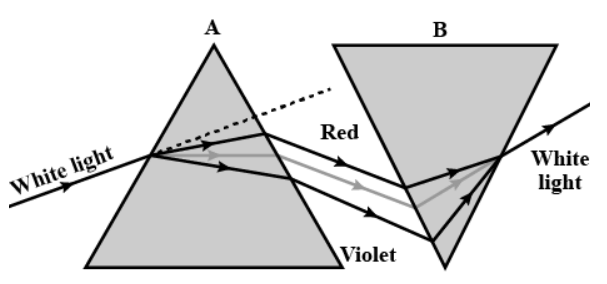
इस घटना से यही पता चलता है की पहला प्रिज्म श्वेत प्रकाश में उपस्थित सभी अवयवी रंगों को विभक्त कर देता है तथा दूसरा प्रिज्म सभी अवयवी रंगों को फिर से मिला श्वेत प्रकाश बना देती है । अतः हम यह कह सकते है की प्रिज्म केवल प्रकाश में उपस्थित अपने अवयवी रंगों विभक्त करती है । ( यह प्रयोग न्यूटन ने किया था )
वर्ण विक्षेपण का कारण
जब प्रकाश निर्वात या वायु में गमन करती है तो इसका वेग होता है , अर्थात इसमें उपस्थित सभी अवयवी रंगों के प्रकाश का वेग भी
होता है । लेकिन जब प्रकाश दूसरे माध्यम में प्रवेश करती है तो माध्यम में भिन्न – भिन्न रंगों ( अर्थात विभिन्न तरंगदैर्घ्यों ) के प्रकाश का वेग भिन्न – भिन्न होता है अतः पदार्थ का अपवर्तनांक भी भिन्न भिन्न रंगों के प्रकाश के लिए भिन्न भिन्न होता है ।
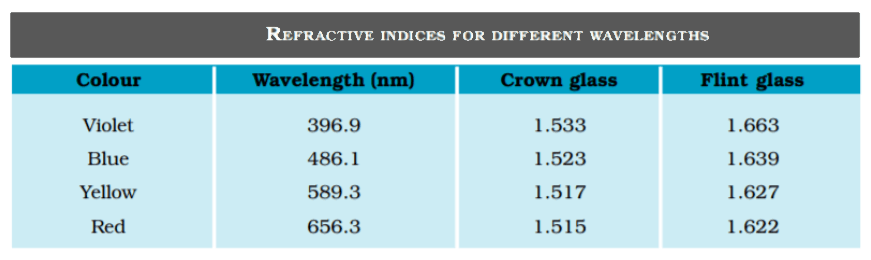
प्रयोग से यह पाया गया है की , किसी माध्यम का अपवर्तनांक आपतित प्रकाश की तरंगदैर्घ्य पर निर्भर करता है ।
( कोची ( cauchy) का समीकरण ) यहाँ A तथा B एक नियतांक है ।
लाल रंग का तरंगदैर्घ्य अधिकतम होता है जबकि बैगनी रंग का तरंगदैर्घ्य न्यूनतम होती है , अर्थात
अर्थात लाल रंग के अपवर्तनांक का मान बैगनी रंग के अपवर्तनांक से कम होता है अर्थात
हम जानते है की पतले कोण वाले प्रिज्म द्वारा उत्पन्न विचलन कोण होता है
बैगनी रंग के लिए और लाल रंग के लिए
अतः बैगनी रंग का विचलन लाल रंग से अधिक होता है ।
NOTE:-
मोटे लेंस को कई प्रिज्मों से बना माना जा सकता है, इसलिए मोटे लेंस प्रकाश के वर्ण विक्षेपण के कारण रंगीन विपथन दिखाते हैं।
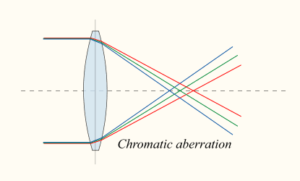
प्रकाश का रंग प्रकाश तरंगों की आवृत्ति पर निर्भर करता है । जब प्रकाश एक माध्यम से दूसरे माध्यम में जाता है , तब उसका वेग एवं तरंगदैर्घ्य बदल जाते है , लेकिन आवृत्ति नहीं बदलती है ।
कोणीय विक्षेपण एवं विक्षेपण क्षमता
कोणीय विक्षेपण :-
जब श्वेत प्रकाश किसी प्रिज्म से गुजरता है तो उसके सीमांत रंगों ( अर्थात लाल और बैगनी रंग ) के विचलन कोणों के अंतर को कोणीय विक्षेपण कहते है । दूसरे शब्दों में लाल रंग तथा बैगनी रंग के बीच के कोण को कोणीय विक्षेपण कहते है । इसे द्वारा निरूपित किया जाता है ।
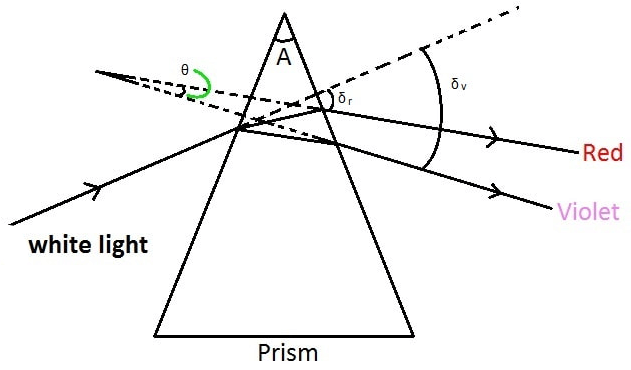
अर्थात, कोणीय विक्षेपण ()=
माना की A प्रिज्म कोण है
लाल रंग के लिए प्रिज्म के पदार्थ का अपवर्तनांक
बैगनी रंग के लिए प्रिज्म के पदार्थ का अपवर्तनांक
पतले कोण वाले प्रिज्म के लिए
विक्षेपण क्षमता :-
किसी पदार्थ द्वारा आपतित श्वेत प्रकाश को उसके अवयवी रंगों में विक्षेपित करने की क्षमता उस पदार्थ की विक्षेपण क्षमता कहलाती है । किसी प्रिज्म की विक्षेपण क्षमता उसके द्वारा उत्पन्न कोणीय विक्षेपण और माध्य विचलन कोण के अनुपात के बराबर होती है । इसे द्वारा सूचित किया जाता है ।
अर्थात 
यहाँ माध्य विचलन का तात्पर्य पिले रंग के प्रकाश के विचलन कोण से है क्योंकि पिले रंग की तरंगदैर्घ्य , प्रकाश की माध्य तरंगदैर्घ्य के बराबर होती है ।
पतले प्रिज्म के लिए
विक्षेपण क्षमता एक विमाहीन राशि है तथा इसकी कोई इकाई नहीं होती है ।
NOTE:-
विक्षेपण क्षमता केवल प्रिज्म के पदार्थ पर ही निर्भर करता है , प्रिज्म कोण पर निर्भर नहीं करता है ।
जब श्वेत प्रकाश किसी प्रिज्म से होकर गुजरता है तो , विचलन के साथ साथ प्रकाश का विक्षेपण भी होता है । यदि दो प्रिज्म को इस प्रकार एक दूसरे के संपर्क में रखा जाये की उनके आधार एक दूसरे के विपरीत हो , तो उन प्रिज़्मों के संयोग से तीन स्थितियां उत्पन्न हो सकती है ।
- कोई विचलन नहीं तथा कोई विक्षेपण नहीं
- विक्षेपण रहित विचलन
- विचलन रहित विक्षेपण
Excersiceएक्साम्प्ले |
प्रश्न() किसी पतले प्रिज्म द्वारा उत्पन्न विचलन कोण किन किन बातों पर निर्भर करता है ? () जब प्रिज्म न्यूनतम विचलन की स्थिति में हो तो आपतन कोण तथा निर्गत कोण में क्या सम्बन्ध होता है । () क्या किसी पतले प्रिज्म द्वारा उत्पन्न विचलन कोण आपतन कोण पर निर्भर करता है ? () प्रिज्म के पदार्थ के अपवर्तनांक का सूत्र न्यूनतम विचलन कोण तथा प्रिज्म कोण के पदों में लिखिए । किसी पतले प्रिज्म से उत्पन्न न्यूनतम विचलन कोण 10° है । प्रिज्म कोण ज्ञात कीजिये । प्रिज्म के पदार्थ का अपवर्तनांक 1.5 है । () प्रिज्म की न्यूनतम विचलन स्थिति से आप क्या समझते है ? प्रिज्म के लिए निम्न सूत्र निर्गमित कीजिये । |
