सभी भौतिक राशियों को साधारणतः दो भागो में विभक्त किया गया है। अदिश राशि तथा सदिश राशि
अदिश राशियाँ (Scalar Quantities):-
जिन भौतिक राशियों को पूर्णतः व्यक्त करने के लिए केवल परिमाण की आवश्यकता होती है , उन्हें अदिश राशियाँ कहते है। जैसे -समय , द्रव्यमान , समय, घनत्व , ऊर्जा इत्यादि
अदिश राशियों को जोड़ने , घटाने , गुणा या भाग करने के लिए साधारण बीजगणित का उपयोग होता है।
सदिश राशियाँ (Vector Quantities):-
जिन भौतिक राशियों को पूर्णतः व्यक्त करने के लिए परिमाण एवं दिशा दोनों की आवश्यकता होती है , उन्हें सदिश राशियाँ कहते है। जैसे बल , विस्थापन , वेग, संवेग इत्यादि
चूँकि सदिशों में दिशा होती है अतः इन्हे सामान्य बीजगणित के नियमों द्वारा जोड़ा, घटाया या गुणा नहीं किया जा सकता है।
सदिशों का निरूपण (Representation of vector):-
सदिश राशि को एक तीर द्वारा निरूपित किया जाता है। जहाँ तीर की लम्बाई उसका परिमाण तथा तीर का नोंक उसकी दिशा को दर्शाती है।
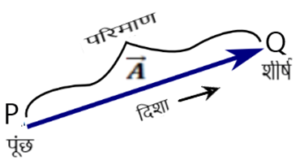
Note:- सदिश के परिमाण को A या द्वारा व्यक्त किया जाता है।
सदिशों के प्रकार :-
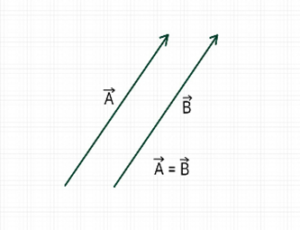
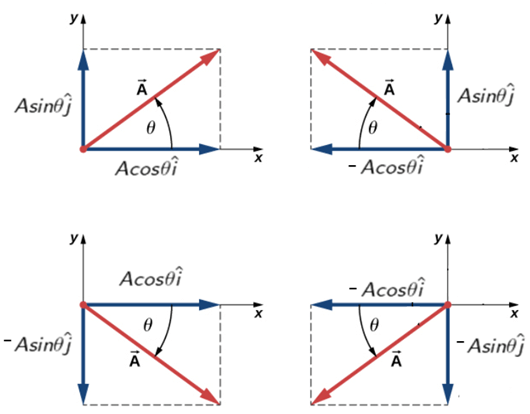
(1). समान सदिश :- जिन सदिशों के परिमाण एवं दिशा समान होते है , उन्हें समान सदिश कहते है।
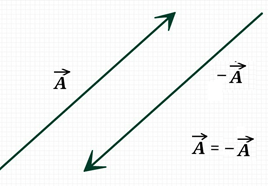
(2) विपरीत सदिश :- जिन सदिशों के परिमाण तो बराबर होते है , लेकिन दिशाएँ परस्पर विपरीत होती है , उन्हें विपरीत सदिश कहते है |
(3) एकांक /इकाई सदिश :- जिस सदिश की दी गई दिशा में परिमाण एकांक (one) होता है उसे इकाई सदिश कहते है
सदिश की दिशा में इकाई सदिश को
से प्रदर्शित किया जाता है।
इकाई सदिश किसी सदिश की दिशा प्रदर्शित करने के लिए प्रयुक्त किया जाता है।
X-अक्ष , Y- अक्ष तथा Z-अक्ष के अनुदिश इकाई सदिश को क्रमशः तथा
से व्यक्त किया जाता है।
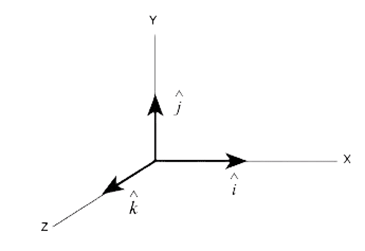
Ex- (5m) सदिश जिसका परिमाण 5m है तथा दिशा X-अक्ष की ओर है।
(4) शून्य सदिश :- जिस सदिश का परिमाण शून्य होता है , उसे शून्य सदिश कहते है। इसकी दिशा का निर्धारण नहीं किया जा सकता।
(5) स्थिति सदिश :- किसी वस्तु की स्थिति को स्थिति सदिश द्वारा भी प्रदर्शित किया जाता है।जिसका प्रारंभिक बिंदु हमेशा मूल बिंदु पर होता है। इसे साधारणतः द्वारा व्यक्त किया जाता है
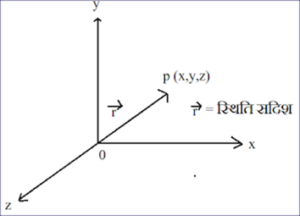
अर्थात P की स्थिति = =
यदि P का निर्देशांक (x,y,z) हो तो
(6) समतलीय सदिश :- जो सदिश एक ही समतल में स्थित होते है , उन्हें समतलीय सदिश कहते है । दो सदिश हमेशा समतलीय सदिश होते है ।
सदिशों का योग (संयोजन )
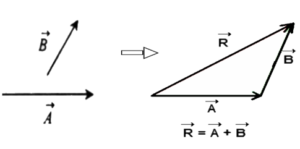
सदिशों के योग का त्रिभुज नियम :-
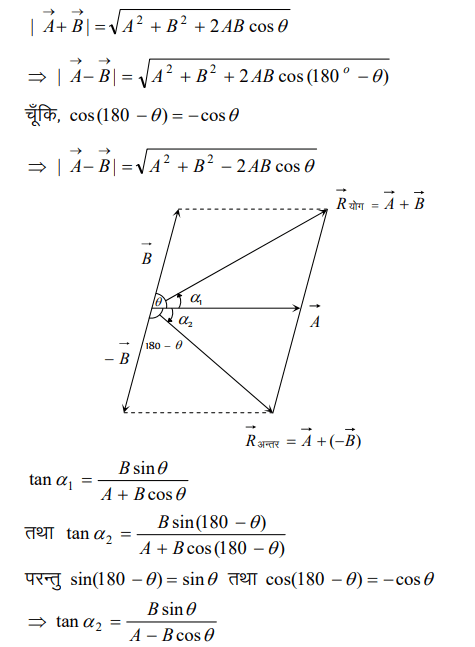
यदि दो सदिश परिमाण एवं दिशा में त्रिभुज की दो क्रमागत भुजाओं को निरूपित करे , तो तीसरी भुजा विपरीत दिशा में परिणामी सदिश को प्रदर्शित करती है।
समान्तर चतुर्भुज का नियम :-
यदि दो सदिशों को परिमाण एवं दिशा में एक समान्तर चतुर्भुज की दो आसन्न भुजाओं से निरूपित किया जाए, तो उनके उभयनिष्ठ बिंदु से गुजरने वाला विकर्ण उनके परिणामी सदिश को प्रदर्शित करता है।
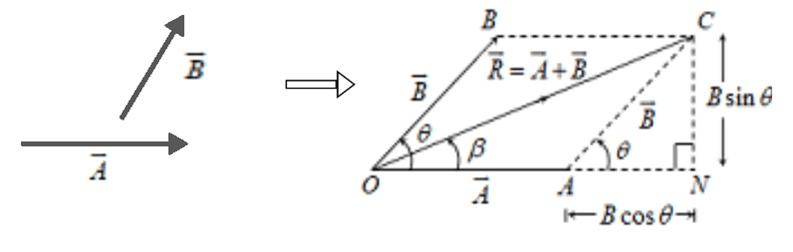
चित्र के अनुसार,
में
यह परिणामी सदिश का परिमाण को व्यक्त करता है
यदि परिणामी सदिश , सदिश
के साथ θ कोण बनाये, तो चित्र के अनुसार
यह परिणामी सदिश की दिशा को व्यक्त करता है।
Special Case:-
(a) जब तथा
एक ही दिशा में हो , अर्थात

( R का अधिकतम मान )
(b) जब तथा
एक दूसरे के विपरीत दिशा में हो , अर्थात ( माना की
)
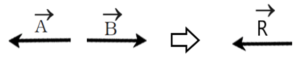
(R का न्यूनतम मान )
(c) जब तथा
एक दूसरे के लंबवत दिशा में हो , अर्थात
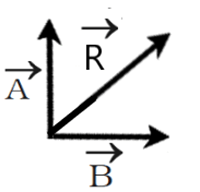
तथा परिणामी का के साथ दिशा होगा
सदिशों के योग का बहुभुज नियम :-
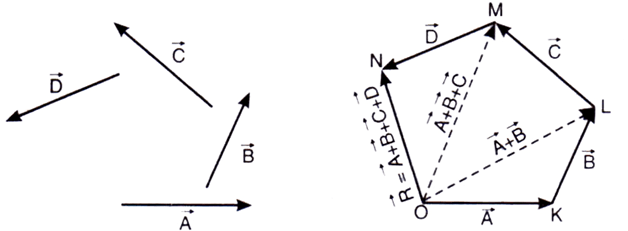
यदि दो से अधिक सदिश परिमाण एवं दिशा में एक बहुभुज की क्रमागत भुजाओं को निरूपित करे, तो बहुभुज की अंतिम भुजा विपरीत दिशा में परिणामी सदिश को प्रदर्शित करती है।
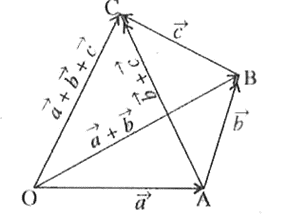
NOTE:- सदिशों का योग साहचर्य नियम का पालन करता है। अर्थात
सदिशों का घटाव : –
सदिश में से सदिश
घटाने का तात्पर्य है , सदिश
में
को जोड़ना
अर्थात

सदिशों का वियोजन :-
किसी सदिश को दो या दो से अधिक सदिशों में विभाजित करने की प्रक्रिया को सदिश का वियोजन कहते है।
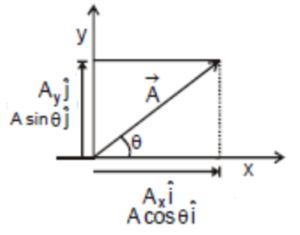
अर्थात , हम लिख सकते है
NOTE:-
1.
2.
3. माना की दो या दो से अधिक सदिश को जोड़ना है , अर्थात , तब आसानी के लिए , जोड़ने से पहले सभी सदिशों को उसके
तथा
घटकों में वियोजित करना चाहिए।
Exercise(1) निम्न में से सत्य और असत्य कथन प्रदर्शित कीजिये । (a) सदिश का परिमाण हमेशा अदिश होता है । (2) यदि एक पिंड पर 6N तथा 8N के दो बल क्रमशः पूर्व दिशा और उत्तर दिशा में कार्य कर रहे है , तो उनका परिणामी ज्ञात करें । ( (3) एक पिंड पर आरोपित 3N तथा 4N बलों का परिणामी बल 5N है । दोनों बलों के बीच का कोण ज्ञात करें । (4)यदि एक पिंड पर लगने वाले दो बालों F और F के परिणामी भी F हो, तो इन दोनों के बीच का कोण क्या होगा । (120°) (5) दो बलों का परिमाण 4N तथा 6N है । यदि इनके बीच का कोण 60° हो , तो बलों का परिणामी एवं दिशा ज्ञात करें । (6) एक कण पर 6N तथा 8N के दो बल परस्पर 90° का कोण बनाते हुए कार्यरत है । सदिश आरेख बनाकर बलों का परिणामी ज्ञात करें । (7) दो बलों के परिमाणों का अनुपात 3 : 5 है तथा परिणामी बल 35 N है । यदि दोनों सदिशों के मध्य कोण 60° है तो प्रत्येक बल का परिमाण ज्ञात कीजिये । (15 N , 25 N ) (8) दो बराबर बल एक दूसरे के लंबवत कार्यरत है । इनका परिणामी बल 14.14 N है । प्रत्येक बल का परिमाण ज्ञात कीजिये । (10N ) (9) दो बल (10) एक व्यक्ति 30m उत्तर , फिर 20m पूर्व तथा फिर 30√2m दक्षिण – पक्षिम चलता है । प्रारंभिक स्थान से उसका विस्थापन कितना होगा ।(10m पक्षिम ) (11) एक कण पर 5N , 4N तथा 3N परिमाण के बल क्रमशः पूर्व , उत्तर तथा पश्चिम दिशा में लग रहे हैं । एक सदिश आरेख बनाकर परिणामी बल का परिमाण एवं दिशा ज्ञात करें । (12) 10m/s की चाल से पूर्व दिशा में चलती हुई एक कार उत्तर दिशा में मुड़ जाती है और उसी चाल से चलती रहती है । कार के वेग में कितना परिवर्तन होगा । (13) एक हवाई जहाज एक वृत्त की परिधि पर 100km/h की चाल से उड़ रहा है । (a) एक चौथाई चक्कर में , (b) आधे चक्कर में वायुयान के वेग में कितना परिवर्तन हो जायेगा ? ( 10√2 km/h, 200 km/h) (14) 60N का एक बल दक्षिण से पक्षिम की ओर 30° के कोण पर कार्य करता है । इसके उत्तर तथा पूर्व दिशा के घटक ज्ञात कीजिये । (15) 80 km/h वेग का एक समकोणिक घटक 40 km/h है तो दूसरा घटक ज्ञात कीजिये । (69.28 km/h) (16) 20N का बल x- अक्ष के साथ 30° का कोण बनाता है । इस बल का x- तथा y- घटक ज्ञात करें । (17) एक बल का क्षैतिज से कोण 30° है । यदि क्षैतिज दिशा में समकोणिक घटक 50N है तो बल का परिमाण और इसका ऊर्ध्वाधर घटक ज्ञात कीजिये । (57.74N, 28.87N) (18) पृथ्वी से एक पतंग की स्थिति सदिश (19) यदि (20) यदि दो अशून्य सदिशों (21) यदि (22) यदि (23) यदि A= 3, B=4 तथा (24) दो सदिशों का परिणामी न्यूनतम तब होता है जब उनके बीच का कोण ________ होता है । (25) दो सदिशों का परिणामी महत्तम तह होता है जब उनके बीच का कोण ________ होता है । (26) जब (27) क्या कोई भी दो अदिश परस्पर जोड़े जा सकते है ? (28) क्या एक सदिश समय के साथ बदल सकता है ? (29) तीन सदिशों का परिणामी शून्य है । आप इन तीनो को किस प्रकार निरूपित करेंगे ? (30) क्या असमान परिमाण के दो सदिशों का योग शून्य हो सकता है । (31) क्या कोई भी दो भिन्न विमाओं वाले सदिश परस्पर जोड़े जा सकते है ? (31) क्या समान विमा वाले एक अदिश तथा एक सदिश को जोड़ा जा सकता है ? (33) क्या तीन असमतलीय सदिशों का परिणाम शून्य हो सकता है ? क्या चार असमतलीय सदिशों का परिणाम शून्य हो सकता है ? (34) अदिश तथा सदिश राशि में अंतर बताएं । (35) सदिशों के योग का समान्तर चतुर्भुज नियम उचित चित्र बनाकर समझाइये । (36) सिद्ध कीजिये की (37) समान सदिश तथा विपरीत सदिश से क्या समझते है । (38) दो बराबर सदिशों के परिणामी का परिमाण कब प्रत्येक के बराबर हो सकता है । (39) दो परस्पर लम्बवत सदिशों (40) दो सदिश (41) |
