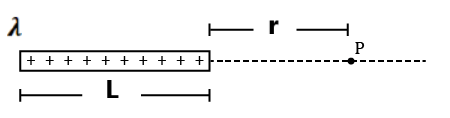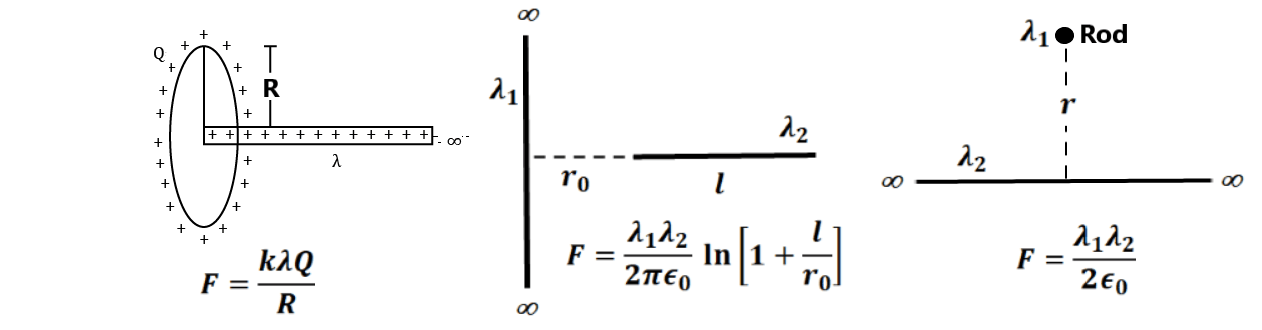Electric Field -

The electric field due to a charge is the space around the charge in which any other charge experiences a force of attraction or repulsion.

Theoretically, an electric field due to a charge extends up to infinity. However, the effect of the electric field dies (vanish) quickly as the distance from the charge is increased.

The strength of an electric field is described by a quantity called electric field intensity or electric field strength. It is defined as the force experienced by unit +ve charge placed at that point or force experienced per unit test charge ( $\dpi{120} \fn_cm q_0$ ). It is denoted by E.

i.e. $\dpi{120} \fn_cm \left [ \vec{E}=\lim_{q_0 \rightarrow 0}\left ( \frac{\vec{F}}{q_0} \right ) \right ]$

It is a scalar quantity and its direction is same as force. Its S.I unit is N/C or V/m

Electric field intensity at a point due to a point charge

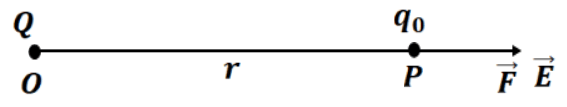
From figure,

force on $\dpi{120} \fn_cm q_0$ due to $\dpi{120} \fn_cm Q$ is given by

$\dpi{120} \fn_cm \vec{F}=\frac{KQq_0}{r^2}\;along\;\vec{OP}$

From the definition, an electric field at a point P is given by

$\dpi{120} \fn_cm \vec{E}=\frac{\vec{F}}{q_0}\;along\;\vec{OP}$

$\dpi{120} \fn_cm \vec{E}=\frac{KQ}{r^2}\;along\;\vec{OP}$

Its magnitude will be

$\dpi{120} \fn_cm \left [ E=\frac{KQ}{r^2} \right ]$

NOTE

(1) The magnitude of electric field strength depends upon the magnitude of charge $\fn_cm Q$ which produces the electric field and not on the value of the test charge $\dpi{120} \fn_cm q_0$ .

(2) Electric field at a point due to group of a point charges ( Superposition principle)

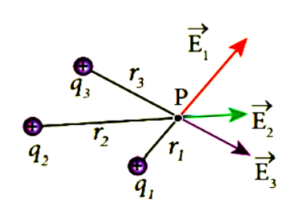
The net electric field strength at point P is $\dpi{120} \fn_cm \left [ \vec{E}_{net}=\vec{E}_1+\vec{E}_2+\vec{E}_3{\color{Red} } \right ]$

(3) If any charge ( $\fn_cm q$ ) is placed at a point where electric field strength is $\fn_cm \vec{E}$ , then force experienced by $\fn_cm q$ is given by $\dpi{120} \fn_cm \left [ \vec{F}=q\vec{E} \right ]$

(4) A charged particle is not affected due to its own field.

(5) Variation of E due to point charge.

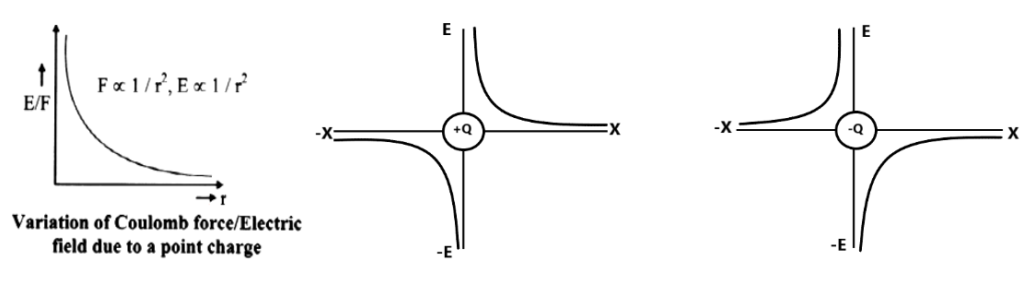
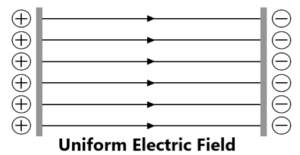
(6) UNIFORM ELECTRIC FIELD:- A space where the electric field is uniform, means the magnitude and direction of electric field strength are the same at every point in space.

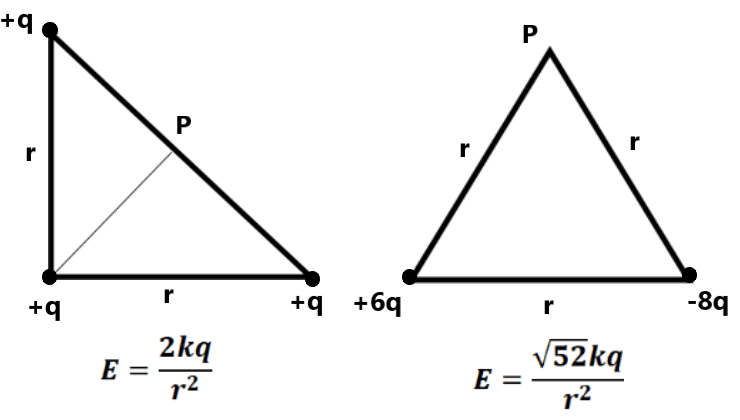
EXERCISE 1

(1) Determine the electric field vector at a distance of 0.50 m from a charge of -2μC. ( $\fn_cm 7.2\times10^4\;N/C$ )

(2) Two point charges $\fn_cm q_1=+0.2 C$ and $\fn_cm q_2=+0.4C$ are placed $\fn_cm 0.1 m$ apart. calculate the electric field.

(a) The midpoint between the charges. ( $\fn_cm 7.2\times10^{11}N/C$ )

(b) A point on the line joining $\fn_cm q_1$ and $\fn_cm q_2$ such that $\fn_cm 0.05 m$ away from $\fn_cm q_2$ and $\fn_cm 0.15m$ away from $\fn_cm q_1$ .( $\fn_cm 1.52\times10^{12}N/C$ )

(3) Two point charges of +16μC and -9μC are placed 8 cm apart in the air. Determine the position of the point at which the resultant field is zero. (24 cm to the right of -9μC )

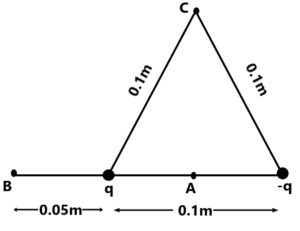
(4) Calculate the electric field at points A, B, and C as shown in fig. where $\fn_cm q=10^{-8}C$ . $\fn_cm (7.2\times10^4 N/C, 3.2\times10^4N/C,9\times10^3 N/C)$

(5) Find the electric field at point P as shown in the figure.

(6) Two identical positive point charges $\fn_cm q$ are placed on the x-axis at x=-a and x=+a, as shown in the figure.

(a) Plot the variation of E along the X-axis.

(b) Plot the variation of E along the Y- axis.

(7) Plot the variation of E along X-axis and Y-axis for the charge distribution as shown in the figure.

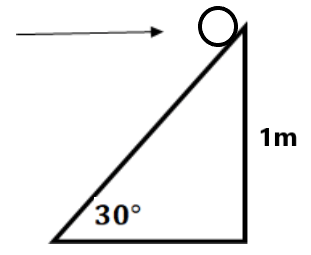
(8) Two-point charges $\fn_cm +5\times10^{-19}C\;and\;+20\times10^{-19}C$ are separated by a distance of 2 m. Find the point on the line joining them at which the electric field intensity is zero. ( x=2/3 cm)

(9) An inclined plane making an angle of 30° with the horizontal is placed in a uniform horizontal electric field of 100 N/C. A particle of mass 1 kg and charge 0.01C is allowed to slide down from rest from a height of 1m. If the co-efficient of friction is 0.2, find the time taken by the particle to reach the bottom. take g=9.8 m/s².

(10) the position vector of two point charges $\fn_cm q_1$ and $\fn_cm q_2$ are $\fn_cm \vec{r}_1\;and\;\vec{r}_2$ respectively. Find the position vector of the point where the net electric field is zero due to these charges. $\fn_cm \left ( \vec{r}=\frac{\vec{r}_1\sqrt{q_2}+\vec{r}_2\sqrt{q_1}}{\sqrt{q}_2+\sqrt{q_1}} \right )$

(11) A point charge of $\fn_cm 0.33\times10^{-8}C$ is placed in a medium of relative permittivity of 5. calculate electric field intensity at a point 10 cm from the charge. ( 525 N/C)

(12) Two point charges $\fn_cm Q_A=3\mu C$ and $\fn_cm Q_A=-3\mu C$ are located 20 cm apart in a vacuum.

(a) What is the electric field at the midpoint of the line joining the two charges? ( $\fn_cm 5.4\times10^6 N/C$ )

(b) If a -ve test charge of magnitude $\fn_cm 1.5\times10^{-9}C$ is placed at this point, What does the test charge experience the force? ( $\fn_cm -8.1\times10^{-3}N$

(13) ABCD is a square of side 5m. Charges of +50μC, -50μC and +50μC are placed at A , C and D respectively. Find the resultant electric field at B. $\dpi{120} \fn_cm (2.7\times10^{10}N/C)$

(14) Four charges +q,+q,-q,-q are placed respectively at the four corners A, B, C and D of a square of side ‘a’. Calculate the electric field at the centre of the square. $\dpi{120} \fn_cm (4\sqrt{2}k\frac{q}{a^2}, 45^0)$

Electric Line of Force / Electric Fields Lines

It is useful to have a kind of “map” that gives the direction and strength of the field at various places. Electric field lines, a concept introduced by Michael Faraday (1791-1867) provide us with an easy way to visualize the electric field. It is an imaginary line but the field is real.

“An electric field line is the path along which a small +ve test charge would move slowly when it is free to do so. ”

Properties of Electric Field Lines

(1) Field lines are continuous curves without any breaks.

(2) The lines of force start at +ve charges and terminate at -ve charges. If there is a single charge, then the lines of force will start or end at infinity.

(3) the tangent to a line of force at any point gives the direction of the net electric field at that point.

(4) No two lines of force can cross each other.

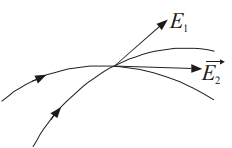
REASON:- If they intersect, then there will be two tangents at that point of intersection and hence two directions of the electric field at the same point, which is not possible.

(5) Electric lines of force are always perpendicular to the surface of a conductor.

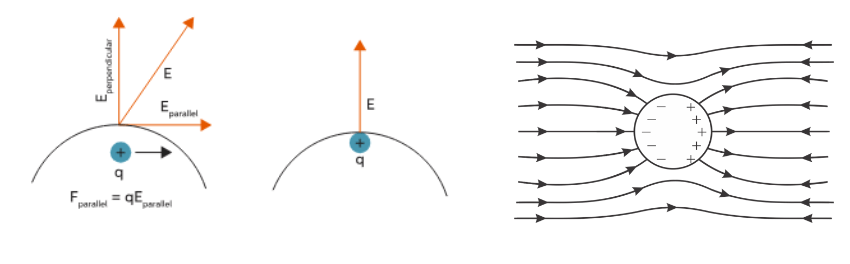
REASON:- If the line of force is not normal to the conductor, the component of the field parallel to the surface would cause the electron to move and would set up a current on the surface. but no current flows in electrostatic.

(6) Electric field lines do not form a closed loop.

REASON:- Because if they do so, then the work done along a closed path will not be zero, which contradicts in conservative nature of the electric field.

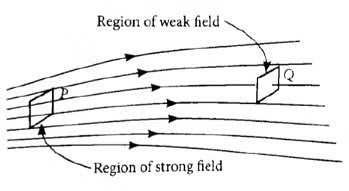
(7) The relative closeness of field lines gives the strength of the electric field.

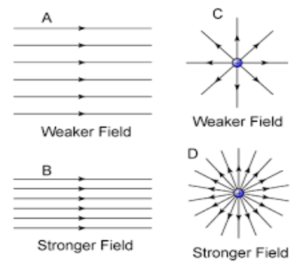
(8) Electric line of force does not pass through the conductor but passes through an insulator.

(9) Electric field strength at a point is proportional to the number of lines passing through normally per unit area. i.e. it is proportional to the flux density.

(10) The number of lines coming from or coming to a charge is proportional to the magnitude of charges.

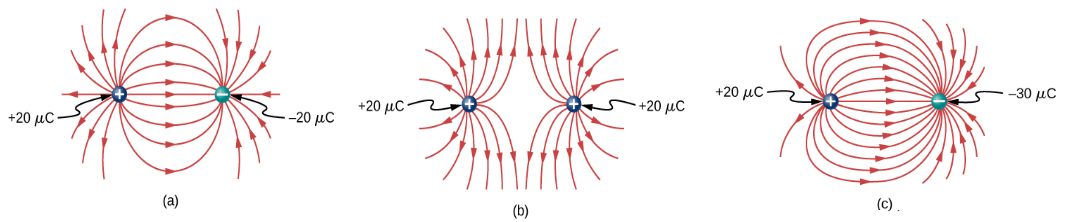
NOTE:

To sketch field lines, pay attention to the following three important points (a) Symmetry (b) Near and far points and (c) The number of lines

EXERCISE 2

(1) Calculate the electric field strength required to just support a water droplet of mass $\dpi{120} \fn_cm 10^{-3}kg$ and have a charge $\dpi{120} \fn_cm 1.6\times 10^{-19}C$ . $\dpi{120} \fn_cm (6.125\times 10^{16} N/C)$

(2) A Positively charged oil drop is prevented from falling under gravity by applying a vertical electric field of 100 V/m. If the mass of the drop is $\dpi{120} \fn_cm 1.6\times10^{-3}g$ , find the number of electrons carried by the drop. $\dpi{120} \fn_cm (10^{12})$

(3) A stream of electrons moving with a velocity of $\dpi{120} \fn_cm 3\times 10^7 m/s$ is deflected by 2 mm in traversing a distance 0f 0.1m in a uniform electric field of strength 10 V/cm. Determine e/m of electrons. $\dpi{120} \fn_cm (2\times10^{11}C/kg)$

(4) A pendulum of mass 80 milligrams carrying a charge of $\dpi{120} \fn_cm 2\times10^{-8}C$ is at rest in a horizontal uniform electric field of $\dpi{120} \fn_cm 2\times 10^4 V/m$ . Find the tension in the thread of the pendulum and the angle it makes with the vertical. $\dpi{120} \fn_cm (8.81\times 10^{-4}N, tan\theta=0.51 \;or\;\theta=27^0)$

(5) A simple pendulum consists of a small sphere of mass m suspended by a thread of length L. The sphere carries a positive charge q. The pendulum is placed in a uniform electric field of strength E directed vertically downwards. Find the period of oscillation of the pendulum due to the electrostatic force acting on the sphere, neglect the effect of the gravitational force. $\dpi{120} \fn_cm \left ( T=2\pi \sqrt{\frac{mL}{qE}} \right )$

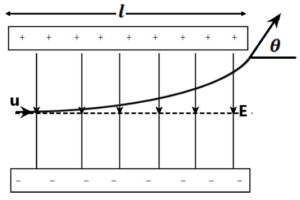
(6) An uniform electric field $\fn_cm E=91\times10^{-6}V/m$ is created between two parallel charged plate as shown in fig. An electron enters the field symmetrically between the plates with a speed $\fn_cm u=4\times10^3 m/s$ . The length of each plate is $\fn_cm l=1m$ . Find the angle of the deviation of the path of the electron as it comes out of the field. (45°)

(7) An electron is projected as in Fig with kinetic energy K, at an angle of 45° between two charged plates. Find the magnitude of the minimum electric field so that the electron just fails to strike the upper plate. (E=k/2qd)

(8) A particle of charge q and mass m moves rectilinearly under the action of an electric field $\fn_cm E=A-Bx$ where A and B are +ve constant and x is the distance from the point where the particle was initially at rest then find the distance travelled by the particle before coming to rest and acceleration of the particle at that moment. $\fn_cm \left ( x=\frac{2A}{B}, a=-\frac{qA}{m} \right )$

(9) A charged cork ball of mass $\fn_cm m$ is suspended on a light string in the presence of a uniform electric field $\fn_cm \vec{E}=(A\hat{i}+B\hat{j})N/C$ , where A and B are +ve numbers, and the ball is in equilibrium at an angle θ from vertical. Find the charge on the ball. $\fn_cm \left ( q=\frac{mg\;tan\theta}{A+B\;tan\theta} \right )$

(10) The bob of a simple pendulum has mass m and carries a charge q on it. The length of the pendulum is L. There is a uniform electric field E in the region. Calculate the time period of small oscillation for the pendulum about its equilibrium position in the following case.

(a) E is vertically down having magnitude E=mg/q
(b) E is vertically up having magnitude E=2mg/q
(c) E is horizontal having magnitude E=mg/q
(d) E has a magnitude of E=√2 mg/q and is directed upward making an angle of 45° with the horizontal.

(11)

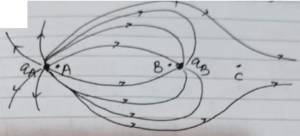
A horizontal electric field towards the right is switched on. Assume elastic collision. Find the time period of the resulting oscillatory motion. Is it a SHM? $\fn_cm \left ( \sqrt{\frac{8md}{qE}} \right )$

(12) A particle of mass m and charge q is thrown at a speed u against a uniform electric field E. How much distance will it travel before coming to momentary rest? $\fn_cm \left ( \frac{mu^2}{2qE} \right )$

(13) The field lines for two-point charges as shown in figure.

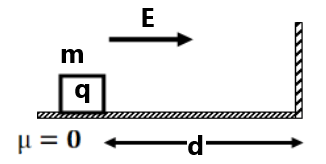
(a) Is the field uniform?
(b) Determine the ratio $\fn_cm \frac{q_A}{q_B}$
(c) If $\fn_cm q_A\;and\;q_B$ are separated by 10(√2-1) cm, find the position of neutral point. (2, 10 cm)

(14) An oil drop of 12 excess electrons is held stationary under a constant electric field of $\fn_cm 2.55\times10^4 N/C$ in Millikan’s oil drop experiment. The density of the oil is 1.26 gram/cm³. Estimate the radius of the drop.

(15) A uniform electric field E exist between two metal plates, one -ve and the other +ve. The plate length is L and the separation of the plates is d.

(a) An electron and proton start from the -ve plate and +ve plate respectively and go to opposite plates. which one of them wins this race?
(b) An electron and a proton start moving parallel to the plates towards the other ends from the midpoint of the separation of plates at one end of the plates. Which of the two will have greater deviation when they come out of the plates, if they start with the (1) same initial velocity (2) Same initial K.E (c) the Same initial momentum

Stable and Unstable equilibrium

The equilibrium of any body of the system means net force and net torque on it must be zero.

After displacing the charged particle from its equilibrium position, if it returns to its mean position due to restoring force, then it is said to be in stable equilibrium, otherwise it is in unstable equilibrium. (at null point E=0)

The potential energy of stable equilibrium is minimum while that of unstable it is maximum.

Electric force/ field due to continuous charge distribution:-

Continuous charges can be distributed on the body either along a line, over a surface or a volume depending upon the shape of the body. When we calculate the force/ field by a continuous distribution of charge, this body consists of a very large number of point charges dq.

The total force/ field due to a small point charge dq is calculated at a point. The force due to the entire charge distribution is found by the integration method.

Charge density:- Charge per unit length/ area/ volume depending upon the distribution of charge.

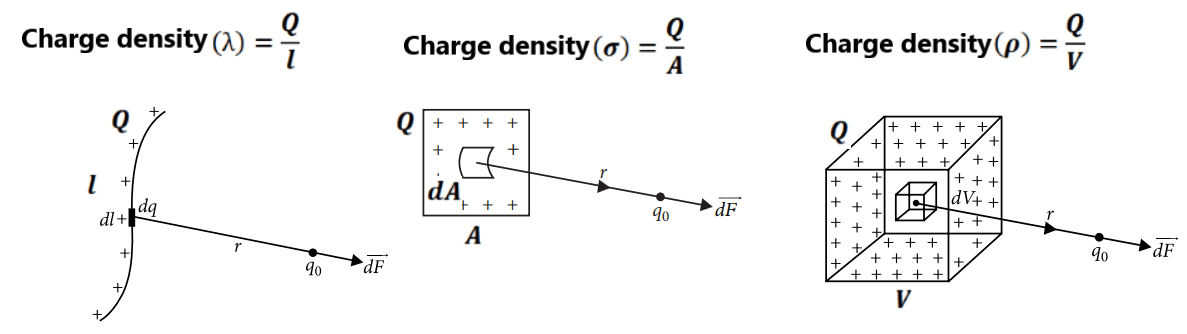
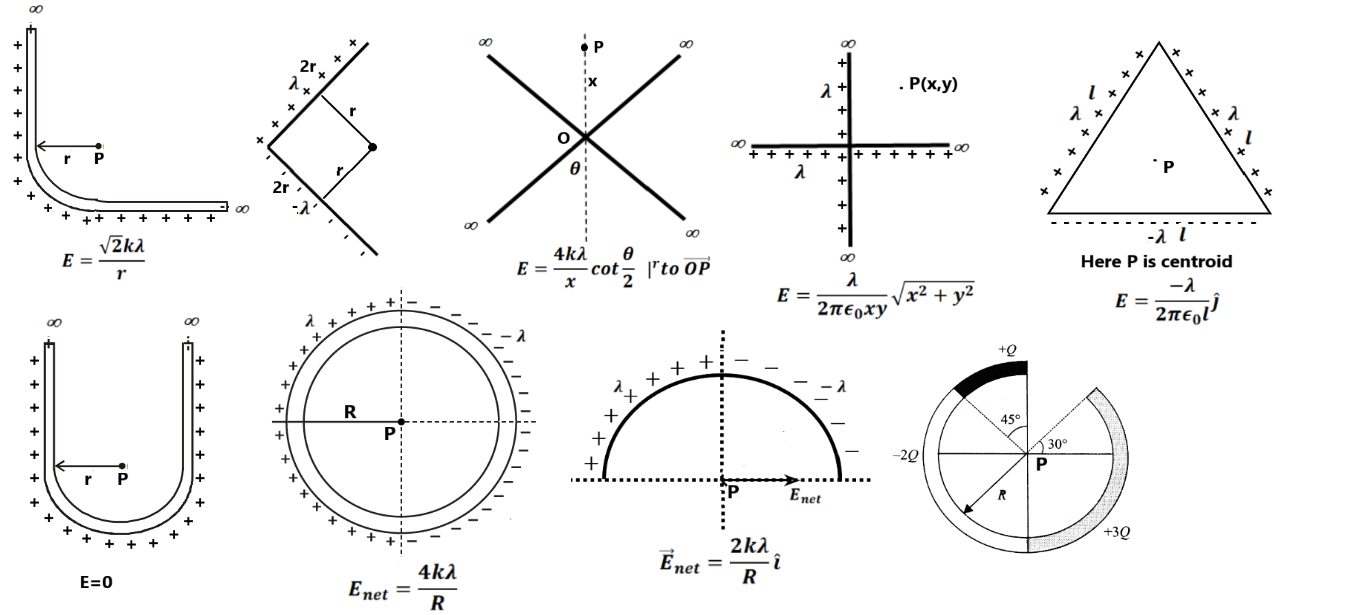
Exercise 3

(1) A metal cube of length 0.1 m is charged by 12μC. Calculate its surface charge density. $\dpi{120} \fn_cm (2\times 10^{-4}C/m^2)$

(2) A uniformly charged sphere carries a total charge of $\dpi{120} \fn_cm 2\pi \times 10^{-12}C$ . Its radius is 5 cm and is placed in a vacuum. Determine its surface charge density. $\dpi{120} \fn_cm (2 \times 10^{-10}C/m^2)$

(3) Two equal spheres of water having equal and similar charges coalesce to form a large sphere. If no charge is lost, how will the surface charge densities of electrification change? $\dpi{120} \fn_cm \left ( \frac{\sigma_1}{\sigma_2}=\frac{2^{2/3}}{2} \right )$

(4) 64 drops of radius 0.02 m and each carrying a charge of 5μC are combined to form a bigger drop. Find how the surface charge density of electrification will change if no charge is lost. $\dpi{120} \fn_cm \left ( \frac{\sigma_1}{\sigma_2}=\frac{1}{4} \right )$

(5) Charge is distributed non-uniformly on line such that linear charge density is given as $\dpi{120} \fn_cm \lambda=ax^2$ . The line charge is kept along x-axis from x=0 to L. Find the total charge on the line. $\fn_cm \left ( \frac{aL^3}{3} \right )$

(6) Charge is distributed non-uniformly on a disc such that surface charge density is given as $\dpi{120} \fn_cm \sigma =ar$ where r is the distance from the centre of the disc and $\fn_cm a=18\mu c/m^3$ . Radius of the disc is 75 cm. Find the total charge on the disc. $\fn_cm \left ( 16\mu C \right )$

(7) Charge is distributed non-uniformly on a sphere such that volume charge density is given as $\dpi{120} \fn_cm \rho =ar$ where $\fn_cm a=8 \mu C/m^4$ and $\fn_cm 0\leq r\leq R$ . Radius of the sphere is R=75 cm. Find the total charge in the sphere. (8μC)

(8) Find the electric field at point P as shown in the figure.

$\fn_cm \left ( E=\frac{K\lambda L}{r(r+L)} \right )$

1. Electric field due to line charge

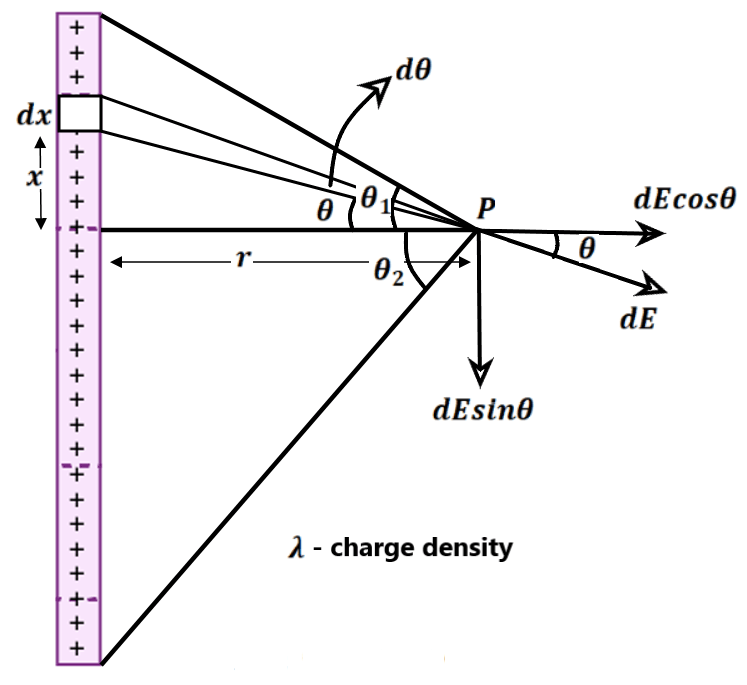
Let λ is the linear charge density of line. Take small strip of length dx as shown in figure

$\dpi{120} \fn_cm dE=\frac{kdq}{\left ( r^2+x^2 \right )}=\frac{k\lambda dx}{\left ( r^2+x^2 \right )}$

$\dpi{120} \fn_cm \because E_y=\int dE cos\theta=\int \frac{k\lambda dx \cos\theta}{(r^2+x^2)}$

$\dpi{120} \fn_cm from\;fig\;\;\;\;\; x=r\tan\theta\;\;\;\;\;dx=r\sec^2\theta d\theta$

$\dpi{120} \fn_cm \therefore E_x=\int \frac{k\lambda r \sec^2 \theta d\theta.\cos\theta}{(r^2+r^2\tan^2\theta)}$

$\dpi{120} \fn_cm =\frac{k\lambda r}{r^2}\int \frac{\sec^2\theta \cos\theta d\theta}{\sec^2\theta}$

$\dpi{120} \fn_cm =\frac{k\lambda r}{r^2}\int_{-\theta_2}^{\theta_1}\cos\theta d\theta=\frac{k\lambda}{r}\left [ sin\theta \right ]_{-\theta_2} ^{\theta_1}$

$\dpi{120} \fn_cm \left [ E_x=\frac{k\lambda}{r}(sin\theta_1+sin\theta_2) \right ]$

$\dpi{120} \fn_cm similarly,$

$\dpi{120} \fn_cm \because E_y=\int dE sin\theta=\int \frac{k\lambda dx \sin\theta}{(r^2+x^2)}$

$\dpi{120} \fn_cm \therefore E_x=\int \frac{k\lambda r \sec^2 \theta d\theta.\sin\theta}{(r^2+r^2\tan^2\theta)}$

$\dpi{120} \fn_cm =\frac{k\lambda r}{r^2}\int \frac{\sec^2\theta \sin\theta d\theta}{\sec^2\theta}$

$\dpi{120} \fn_cm =\frac{k\lambda r}{r^2}\int_{-\theta_2}^{\theta_1}\sin\theta d\theta=\frac{k\lambda}{r}\left [ -cos\theta \right ]_{-\theta_2} ^{\theta_1}$

$\dpi{120} \fn_cm \left [ E_y=\frac{k\lambda}{r}(cos\theta_2-cos\theta_1) \right ]$

∴ The net electric field at point P is given by $\dpi{120} \fn_cm \vec{E}=\vec{E}_x+\vec{E}_y$

$\dpi{120} \fn_cm \mathbf{\therefore \left [ E=\sqrt{E^2_x+E_y^2} \right ]}$ if we solve it then $\dpi{120} \fn_cm \mathbf{\left [ E=\frac{\sqrt{2}k\lambda}{r}\sqrt{1-cos(\theta_1+\theta_2)} \right ]}$

Special Case:-

(a) For equatorial position

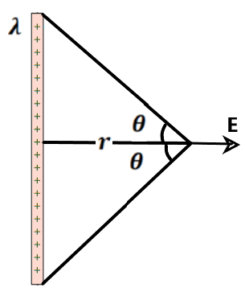
Here $\dpi{120} \fn_cm \theta_1=\theta_2=\theta$

$\dpi{120} \fn_cm E_x=\frac{k\lambda}{r}2\sin\theta\;\;\;and\;\;\;E_y=0$

$\dpi{120} \fn_cm \therefore E=\sqrt{\left ( \frac{2k\lambda\sin\theta}{r} \right )^2+0^2}$

$\dpi{120} \fn_cm \left [ E=\frac{2k\lambda}{r}\sin\theta \right ]\;\;\;along\;x\;axis$

(b) For semi-infinite wire

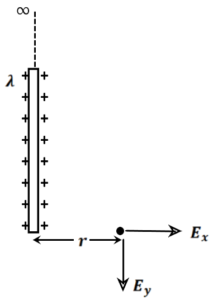
here

$\dpi{120} \fn_cm (\theta_2\rightarrow 0\;\;and\;\; \theta_1\rightarrow 90^0)$

i.e.

$\dpi{120} \fn_cm E_x=\frac{k\lambda}{r}(\sin90^0+\sin0^0)=\frac{k\lambda}{r}$

and

$\dpi{120} \fn_cm E_y=\frac{k\lambda}{r}(\cos0^0-\cos90^0)=\frac{k\lambda}{r}$

$\dpi{120} \fn_cm \therefore E=\sqrt{E_x^2+E_y^2}=\sqrt{\left ( \frac{k\lambda}{r} \right )^{2}+\left ( \frac{k\lambda}{r} \right )^{2}}$

$\dpi{120} \fn_cm \mathbf{\left [ E=\frac{\sqrt{2}k\lambda}{r} \right ]}$

(c) For infinite wire

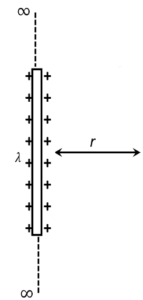
here $\dpi{120} \fn_cm \left ( \theta_2\rightarrow 90^0\;\;\;and\;\;\; \theta_1\rightarrow 90^0 \right )$

$\dpi{120} \fn_cm E_x=\frac{2k\lambda}{r}\;\;\;and\;\;\;E_y=0$

$\dpi{120} \fn_cm \therefore \mathbf{\left [ E=\frac{2k\lambda}{r} \right ]}$

(d) Example

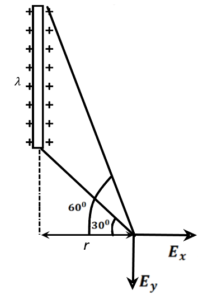
Here take $\dpi{120} \fn_cm \theta_1=60^0$ and $\dpi{120} \fn_cm \theta_2=-30^0$ (in derivation $\dpi{120} \fn_cm \theta_2$ was anticlockwise but here is clockwise so we take $\dpi{120} \fn_cm \theta_2$ -ve)

$\dpi{120} \fn_cm E_x=E_y=\frac{k\lambda(\sqrt{3}-1)}{2r}$

2. Electric field at the centre due to charged circular arc

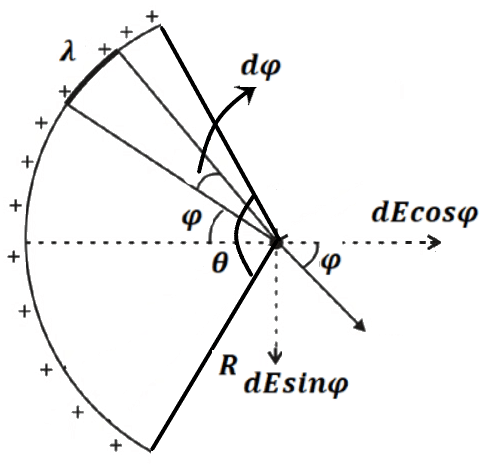
Let $\dpi{120} \fn_cm \lambda\rightarrow$ linear charge density, then $\dpi{120} \fn_cm dq=\lambda(Rd\Phi)$

from figure $\dpi{120} \fn_cm \int dE\sin\Phi=0$

$\dpi{120} \fn_cm \therefore$ The net electric field at a point P ( Centre) is given by

$\dpi{120} \fn_cm E=\int dE\cos\Phi$

$\dpi{120} \fn_cm =\int \frac{kdq}{R^2}\cos\Phi$

$\dpi{120} \fn_cm =\frac{k\lambda Rd\Phi\cos\Phi}{R^2}$

$\dpi{120} \fn_cm =\frac{k\lambda}{R}\int_{-\frac{\theta}{2}}^{\frac{\theta}{2}}\cos\Phi d\Phi$

$\dpi{120} \fn_cm =\frac{k\lambda}{R}\left [ \sin\Phi \right ]_{-\frac{\theta}{2}}^{\;\frac{\theta}{2}}$

$\dpi{120} \fn_cm E=\frac{k\lambda}{R}\left ( \sin\frac{\theta}{2}+\sin\frac{\theta}{2} \right )$

$\dpi{120} \fn_cm \mathbf{\left [ E=\frac{2k\lambda\sin\frac{\theta}{2}}{R} \right ]}$

Special Case:

(a) For Quadrant $\dpi{120} \fn_cm \theta=\frac{\pi}{2}\;\;\;\therefore \mathbf{\left [ E=\frac{\sqrt{2}k\lambda}{R} \right ]}$

(b) For semi-circle $\dpi{120} \fn_cm \theta=\pi\;\;\;\therefore \mathbf{\left [ E=\frac{2k\lambda}{R} \right ]}$

(c) For complete circle $\dpi{120} \fn_cm \theta=2\pi\;\;\;\therefore \mathbf{\left [ E=0 \right ]}$

3. Electric field due to a uniformly charged ring on its axis

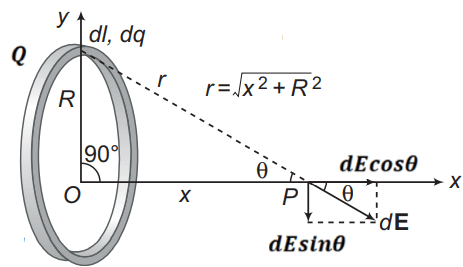
The electric field at point P due to a small charge $\dpi{120} \fn_cm dq$ is $\dpi{120} \fn_cm dE=\frac{kdq}{(x^2+R^2)}$

From fig $\dpi{120} \fn_cm \int dE\sin\theta=0$

$\dpi{120} \fn_cm \therefore$ The net electric field at point P due to the ring is

$\dpi{120} \fn_cm E=\int dE\cos\theta=\int \frac{kdq}{(x^2+R^2)}\cos\theta$

$\dpi{120} \fn_cm E=\int\frac{kdq}{(x^2+R^2)}.\frac{x}{(x^2+R^2)^{\frac{1}{2}}}=\frac{kx}{(R^2+x^2)^{\frac{3}{2}}}\int dq$

$\dpi{120} \fn_cm \mathbf{\therefore \left [ E=\frac{kQx}{(R^2+x^2)^{\frac{3}{2}}} \right ]}$

Special case:

(a) At the centre of the ring x=0 ∴ E=0

(b) For point very close to the centre i.e. x<<R

$\dpi{120} \fn_cm i.e. \;\;(R^2+x^2)\approx R^2$

$\dpi{120} \fn_cm \therefore \mathbf{\left [ E=\frac{kQ}{R^3}x \right ]}\;\;\;\Rightarrow \;\;\;\mathbf{E\propto x}$

(c) For point far away from the centre of the ring i.e. x>>R

$\dpi{120} \fn_cm i.e.\;\;(R^2+x^2)\approx x^2$

$\dpi{120} \fn_cm \therefore E=\frac{kQx}{x^3}\;\;\;\Rightarrow \;\;\;\mathbf{\left [ E=\frac{kQ}{x^2} \right ]}\;\;\;\Rightarrow \;\;\;E\propto \frac{1}{x^2}$

The ring behaves as a point charge kept at its centre.

(d) For maximum electric field

$\dpi{120} \fn_cm \frac{dE}{dx}=0,\;\;\;\;\;Solve\;it\;and\;get\;\mathbf{\left [ x=\pm \frac{R}{\sqrt{2}} \right ]}$

4. Electric field due to a uniformly charged non-conducting disc on its axis:

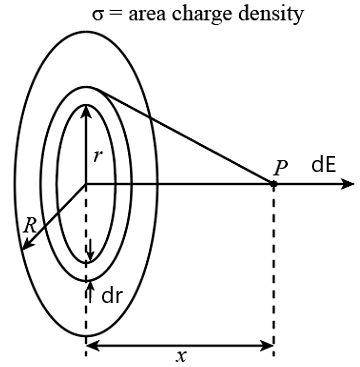
Consider a ring of radius r and thickness dr. The charge on this ring is $\dpi{120} \fn_cm dq=\sigma 2\pi rdr$

The electric field at point P due to this ring is given by

$\dpi{120} \fn_cm dE=\frac{kdq \;x}{(r^2+x^2)^{\frac{3}{2}}}=\frac{k(\sigma2\pi rdr)x}{(r^2+x^2)^{\frac{3}{2}}}$

∴ The net electric field at point P due to the disc is

$\dpi{120} \fn_cm E=k\pi \sigma x\int_{0}^{R}\frac{2rdr}{(r^2+x^2)\frac{3}{2}}$

put $\dpi{120} \fn_cm z=r^2+x^2\;\;or\;\;z^2=r^2+x^2\;\;\;and\;solve\;it\;we\;get$

$\dpi{120} \fn_cm \mathbf{\left [ E=\frac{\sigma}{2\varepsilon_0}\left ( 1-\frac{x}{\sqrt{R^2+x^2}} \right ) \right ]}$

Special case

(a) if x>>R

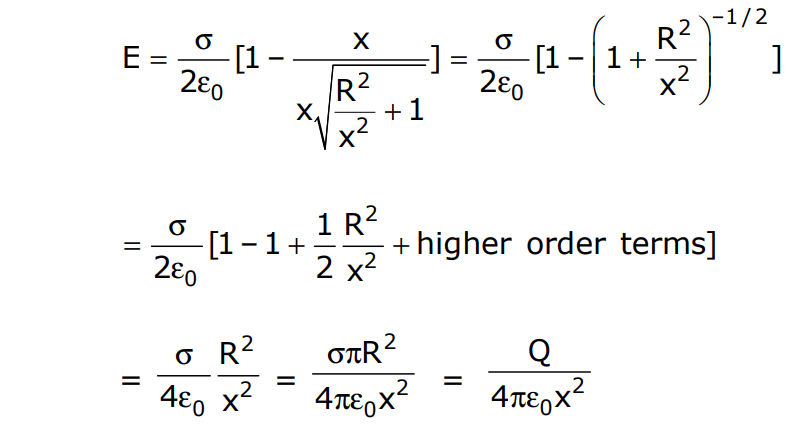
i.e. behaviour of the disc is like a point charge

(b) If x<<R , then we can write $\dpi{120} \fn_cm \frac{x}{\sqrt{R^2+x^2}}\approx 0$

i.e. $\dpi{120} \fn_cm E=\frac{\sigma}{2\epsilon_0}(1-0)$

$\dpi{120} \fn_cm \mathbf{\left [ E=\frac{\sigma}{2\epsilon_0} \right ]}$

i.e. behaviour of the disc is like an infinite sheet of charge

5. Electric field due to charged Hollow hemisphere on its centre:

We know that a hollow sphere is a collection of small rings. If $\dpi{120} \fn_cm \sigma$ the volume charge density of hollow hemisphere.

Then, from the figure charge on a small ring is $\dpi{120} \fn_cm dq=\sigma(2\pi R\sin\theta.Rd\theta)=\sigma 2\pi R^2\sin\theta d\theta$

$\dpi{120} \fn_cm \therefore$ The electric field at the centre due to this ring is

$\dpi{120} \fn_cm dE=\frac{kdq(R\cos\theta)}{\left ( R^2sin^2\theta+R^2cos^2\theta \right )^{\frac{3}{2}}}$

$\dpi{120} \fn_cm dE=\frac{k\sigma 2\pi R^2sin\theta d\theta.R cos\theta}{R^3}$

$\dpi{120} \fn_cm dE=k\pi \sigma \sin2\theta d\theta$

$\dpi{120} \fn_cm \therefore$ The net electric field at the centre due to the hollow hemisphere is

$\dpi{120} \fn_cm E=\pi k \sigma \int_{0}^{\pi /2}sin2\theta d\theta$ solve it , we get

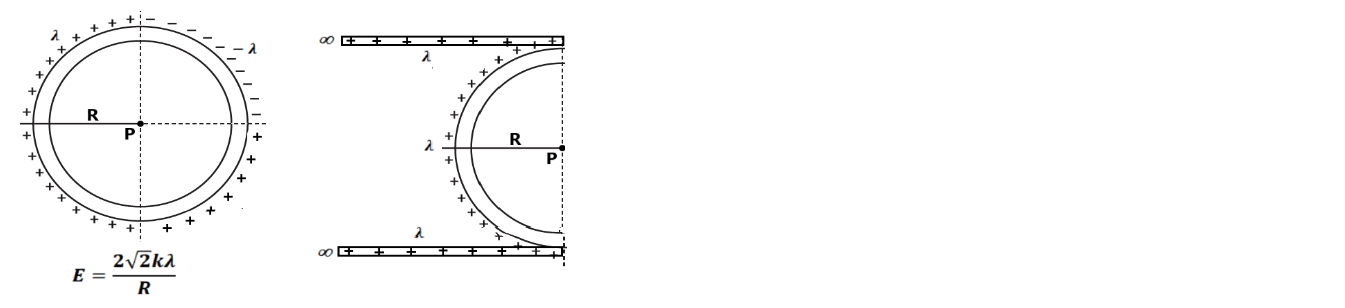
$\dpi{120} \fn_cm \mathbf{\left [ E=\frac{\sigma}{4\epsilon_0} \right ]}$

Exercise 4

1. Find the electric field at point P as shown in the figure.

2. Find the force of interaction between the line charge and the ring.

3. A circular wire loop of radius r carries a total charge Q distributed uniformly over its length. A small length dl of the wire is cut off. Find the electric field at the centre due to the remaining wire. $\dpi{120} \fn_cm \left ( \frac{Qdl}{8\pi^2\epsilon _0 r^3} \right )$

4. Positive charge Q is distributed uniformly over a circular ring of radius R. A particle having a mass m and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x<<R, find the time period of oscillation of the particle if it is released from there.

5. A 10 cm long rod carries a charge of +50μC distributed uniformly along its length. Find the magnitude of the electric field at a point 10 cm from both ends of the rod. $\dpi{120} \fn_cm \left [ 5.2\times10^7N/C \right ]$

6. A ring of radius R is with a uniformly distributed charge Q on it. A charge q is now placed at the centre of the ring. Find the increase in tension in the ring. $\dpi{120} \fn_cm \left ( \Delta T=\frac{kqQ}{2\pi R^2} \right )$

7. If the charge is slightly displaced perpendicular to the wire from its equilibrium position then find out the time period of S.H.M.

$\dpi{120} \fn_cm \left ( T=2\pi \sqrt{\frac{md^2}{2k\lambda q}} \right )$