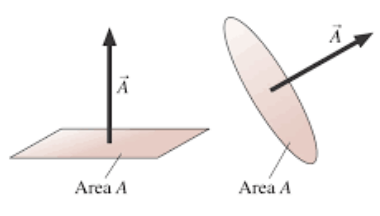
क्षेत्रफल सदिश :-
चूँकि क्षेत्रफल एक अदिश राशि है लेकिन बहुत जगह इसे सदिश द्वारा प्रदर्शित किया जाता है । जिसकी दिशा पृष्ठ के लंबवत बाहर की ओर होती है ।
विधुत फ्लक्स :-
किसी भी पृष्ठ से गुजरने वाली विधुत बल रेखाओं की संख्या उस पृष्ठ का विधुत फ्लक्स कहलाता है । इसे Φ द्वारा सूचित किया जाता है । यदि कोई क्षेत्रफल सदिश है तथा
उस क्षेत्रफल के सभी बिंदु पर विधुत क्षेत्र की तीव्रता है , तो उस क्षेत्रफल द्वारा विधुत फ्लक्स का मान इस प्रकार होगा ।
जहाँ θ , तथा
के बीच का कोण है ।

NOTE:-यह सूत्र तभी मान्य होगा जब पृष्ठ सपाट हो तथा पृष्ठ के हरेक बिंदु पर विधुत क्षेत्र की तीव्रता समान हो , अन्यथा Integration Technique द्वारा कुल फ्लक्स का मान ज्ञात किया जा सकता है । |
यह एक अदिश राशि है तथा इसका S.I मात्रक होता है , इसका विमीय सूत्र
होता है ।
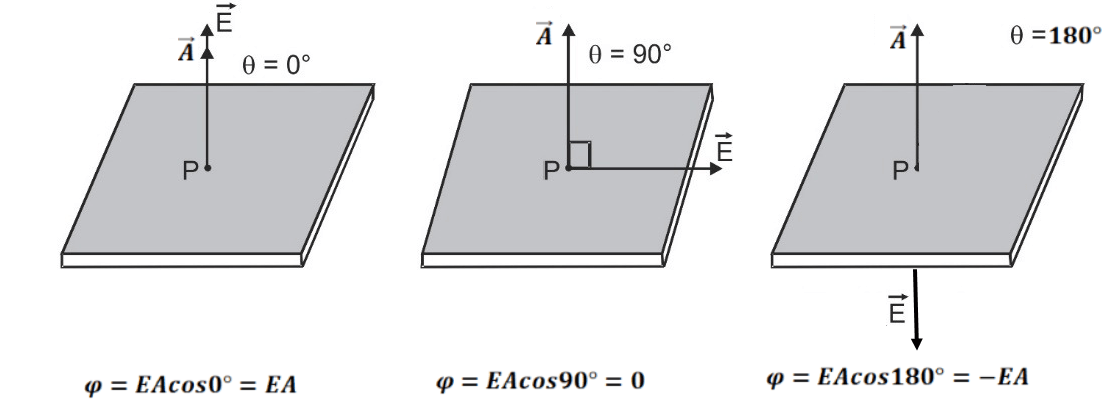
यदि θ=0°, तब Φ=0 , यदि θ<90°, तब Φ=+ve, यदि θ>90°, तब Φ=-ve
अर्थात यदि बल रेखाएं पृष्ठ से बाहर निकल निकल रही हो , तो फ्लक्स +ve होता है तथा यदि बल रेखाएं पृष्ठ में प्रवेश कर रही हो , तो फ्लक्स -ve होता है ।
गॉस का प्रमेय :-
गॉस के प्रमेय के अनुसार निर्वात में किसी बंद पृष्ठ में से कुल विधुत फ्लक्स का मान पृष्ठ द्वारा घेरे गए कुल आवेश के गुणा के बराबर होता है ।
अर्थात ,
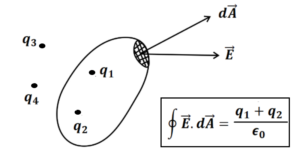
NOTE:- समीकरण में बाएं तरफ विधुत क्षेत्र की तीव्रता (E) पृष्ठ के अंदर तथा बाहर दोनों आवेशों के कारण होता है लेकिन दाएं तरफ केवल पृष्ठ के अंदर का आवेश होता है ।
किसी सरल रेखीय आवेश के कारण विधुत क्षेत्र के तीव्रता :-
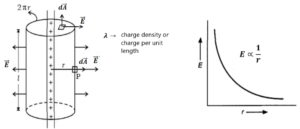
माना की एक बहुत लम्बा तथा एक समान रूप से आवेशित छड़ है जिसके प्रति एकांक लम्बाई पर आवेश है । छड़ से r दुरी पर एक बिंदु P है जहाँ पर छड़ के कारण विधुत क्षेत्र की तीव्रता ज्ञात करनी है ।
छड़ के समाक्षीय l लम्बाई तथा r त्रिज्या के एक बंद बेलनाकार सतह की कल्पना करते है जो P से होकर गुजरता है इसे गॉसियन सतह कहते है।
माना की P बिंदु पर विधुत क्षेत्र की तीव्रता E है । बेलन के वक्र भाग में P बिंदु पर एक छोटे से क्षेत्रफल सदिश के कारण विधुत फ्लक्स होगा।
∴ पुरे वक्र भाग के लिए विधुत फ्लक्स का मान होगा
बेलन के समतल सतह के कारण विधुत फ्लक्स का मान शून्य होगा क्योंकि क्षेत्रफल सदिश तथा विधुत बल रेखाएँ एक दूसरे के लम्बवत है ।
अतः गॉसियन सतह के कारण कुल विधुत फ्लक्स का मान होगा ।
गॉस के प्रमेय के अनुसार , गॉसियन सतह के कारण कुल विधुत फ्लक्स होगा ।
समीकरण (1) और (2) से
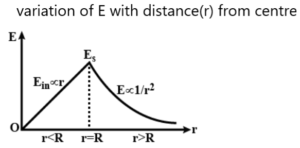
किसी समान रूप से आवेशित खोखले गोले के कारण किसी बिंदु पर विधुत क्षेत्र की तीव्रता :-
माना की एक एकसमान रूप से आवेशित एक खोखला गोला है जिसकी त्रिज्या R तथा आवेश Q है । गोले के केंद्र से r दुरी पर एक बिंदु P है जहाँ पर विधुत क्षेत्र की तीव्रता ज्ञात करनी है ।
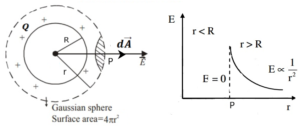
CASE 1:- जब बिंदु गोले के बाहर स्थित हो
गॉसियन सतह के P बिंदु पर एक छोटे से क्षेत्रफल सदिश के कारण विधुत क्षेत्र की तीव्रता होगी ।
∴ गॉसियन सतह के कारण कुल विधुत फ्लक्स का मान होगा ।
गॉस के अनुसार
समीकरण (1) और (2) से
CASE 2:- जब बिंदु गोले के अंदर स्थित हो
चूँकि गोले के अंदर कोई भी आवेश स्थित नहीं है , अतः अगर खोखले गोले के अंदर गॉसियन पृष्ठ खिंचा जाता है तो उससे होकर गुजरने वाले विधुत फ्लक्स का मान शून्य होगा , क्योंकि
यदि गोले के अंदर गॉसियन पृष्ठ के किसी बिंदु पर विधुत क्षेत्र की तीव्रता हो तो गॉसियन पृष्ठ द्वारा कुल फ्लक्स का मान होगा
समीकरण (1) और (2) से
अतः आवेशित खोखले गोले के अंदर विधुत क्षेत्र की तीव्रता शून्य होती है ।
किसी एकसमान रूप से ठोस आवेशित गोले के कारण किसी बिंदु पर विधुत क्षेत्र की तीव्रता :-
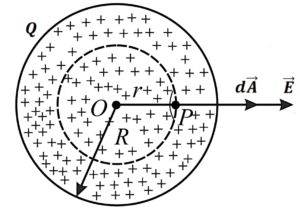
CASE 1:- जब बिंदु गोले के अंदर स्थित हो
माना की किसी ठोस गोले के अंदर एक बिंदु P है जिसकी केंद्र o से दुरी r है । o को केंद्र मानते हुए r त्रिज्या का एक गॉसियन पृष्ठ का निर्माण करते है ।
गॉसियन पृष्ठ के अंदर आवेश होगा
आयतन घनत्व × गॉसियन गोले का आयतन
गॉसियन सतह के P बिंदु पर एक छोटे से क्षेत्रफल सदिश के कारण विधुत क्षेत्र की तीव्रता होगी ।
∴ गॉसियन सतह के कारण कुल विधुत फ्लक्स का मान होगा ।
गॉस के अनुसार
समीकरण (1) और (2) से
CASE 2:- जब बिंदु गोले के बाहर स्थित हो
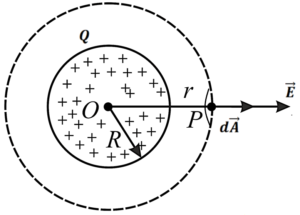
माना की किसी ठोस गोले के बाहर एक बिंदु P है जिसकी केंद्र o से दुरी r है । o को केंद्र मानते हुए r त्रिज्या का एक गॉसियन पृष्ठ का निर्माण करते है ।
गॉसियन सतह के P बिंदु पर एक छोटे से क्षेत्रफल सदिश के कारण विधुत क्षेत्र की तीव्रता होगी ।
∴ गॉसियन सतह के कारण कुल विधुत फ्लक्स का मान होगा ।
गॉस के अनुसार
समीकरण (1) और (2) से
NOTE:-
अनन्त आवेश विस्तार की समतल चादर के कारण विधुत क्षेत्र की तीव्रता :-
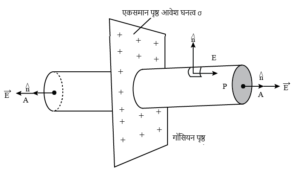
माना की एक पतली अनन्त क्षेत्रफल का कुचालक समतल चद्दर है , जिसका एकसमान पृष्ठ आवेश घनत्व σ है । चद्दर से r दुरी पर एक बिंदु P है जहां पर विधुत क्षेत्र की तीव्रता ज्ञात करनी है । P सतह से गुजरती हुई एक गॉसियन पृष्ठ का निर्माण करते है जो की एक बंद खोखले बेलन की तरह है , जैसा की चित्र में दिखाया गया है ।
गॉसियन पृष्ठ को तीन भागों में विभाजित किया जा सकता है जो की दोनों सिरों के समतल पृष्ठ ( जिसका क्षेत्रफल A है ) तथा बेलन का वक्रीय पृष्ठ है । माना की P बिंदु पर विधुत क्षेत्र की तीव्रता E है ।
बेलन के वक्रीय सतह के कारण विधुत फ्लक्स का मान शून्य होगा क्योंकि हर जगह क्षेत्रफल सदिश तथा विधुत बल रेखाएँ एक दूसरे के लम्बवत है ।
बेलन के दोनों समतल पृष्ठ के कारण समान विधुत फ्लक्स होगा ।
∴ पुरे बेलन के कारण कुल विधुत फ्लक्स होगा
गॉस के प्रमेय के अनुसार
समीकरण (1) और (2) से
यहाँ पर विधुत क्षेत्र की तीव्रता दुरी पर निर्भर नहीं करती है ।
गॉस की प्रमेय के द्वारा कूलम्ब के नियम की निष्पत्ति:-

r दुरी पर स्थित दो बिंदु आवेशों q1 तथा q2 पर विचार करते है । q1 की स्थिति को केंद्र मानकर r त्रिज्या का एक वृत्त का निर्माण करते है जो गॉसियन सतह कहलाता है । माना की गॉसियन सतह के किसी बिंदु पर विधुत क्षेत्र की तीव्रता E है ।
गॉसियन सतह के किसी छोटे से क्षेत्रफल dA के कारण विधुत फ्लक्स का मान होगा
गॉसियन सतह के कारण कुल विधुत फ्लक्स का मान होगा
गॉस के अनुसार कुल विधुत फ्लक्स का मान होगा
समीकरण (1) और (2) से
विधुत क्षेत्र का यह मान गॉसियन पृष्ठ के सभी बिंदु पर समान है अतः वह बिंदु जहाँ आवेश q2 है वहां भी बिधुत क्षेत्र की तीव्रता है ।
अतः q2 पर लगने वाला बल होगा
यह व्यंजक कूलम्ब के नियम का गणितीय रूप है ।
