प्रकाश का विवर्तन (Diffraction of Light) -

किसी अवरोध के किनारों अथवा द्वारक से उत्पन्न उत्पन्न हुई अवरोध की ज्यामितीय छाया में प्रकाश के मुड़ने की घटना को प्रकाश का विवर्तन कहते है । यह तरंग गति का एक लक्षण है।

विवर्तन की घटना प्रायः सभी प्रकार के तरंगों के द्वारा होती है । जैसे ध्वनि तरंग , प्रकाश तरंग, द्रव तरंग इत्यादि

तरंग का स्पष्ट विवर्तन के लिए अवरोध या द्वारक का आकार तरंगदैर्घ्य की कोटि का होना चाहिए । जब अवरोधक या द्वारक के आकार को कम किया जाता है तो इसका आकार प्रकाश की तरंगदैर्घ्य के समतुल्य हो जाता है तथा प्रकाश का विवर्तन अधिक स्पष्ट दिखाई देता है ।

यदि अवरोध अथवा द्वारक का आकार बहुत छोटा हो तो ज्यामितीय छाया के अंदर के भाग में प्रदीप्त एका- एक समाप्त नहीं होती, बल्कि अंदर की ओर धीरे धीरे घटती हुई समाप्त होती है । ज्यामितीय छाया के क्षेत्र में प्रदीप्त तभी संभव है जब अवरोधक के किनारों से प्रकाश की किरणे मुड़कर ज्यामितीय छाया के क्षेत्र में पहुँच जाए ।

तीक्ष्ण किनारों पर प्रकाश तरंगों के आंशिक रूप से मुड़ने की घटना को ही प्रकाश का विवर्तन कहते है ।

NOTE:- किरण प्रकाशिकी में विवर्तन की घटना को ignore( अनदेखा ) करके प्रकाश को सीधी रेखा में गतिमान माना जाता है ।

विवर्तन के प्रकार

फ्रेनल विवर्तन :- इस प्रकार के विवर्तन में स्रोत तथा पर्दा दोनों ही अवरोध अथवा द्वारक से एक निश्चित दुरी पर होते है .
फ्रॉनहॉफर विवर्तन : – इसमें अवरोध या द्वारक से स्रोत तथा पर्दे की दुरी अनंत होती है । इस घटना में, अनंत दुरी पर रखे स्रोत से प्राप्त प्रकाश को विवर्तन के पश्चात् उत्तल लेंस का प्रयोग करते हुए पर्दे पर केंद्रित करते है।

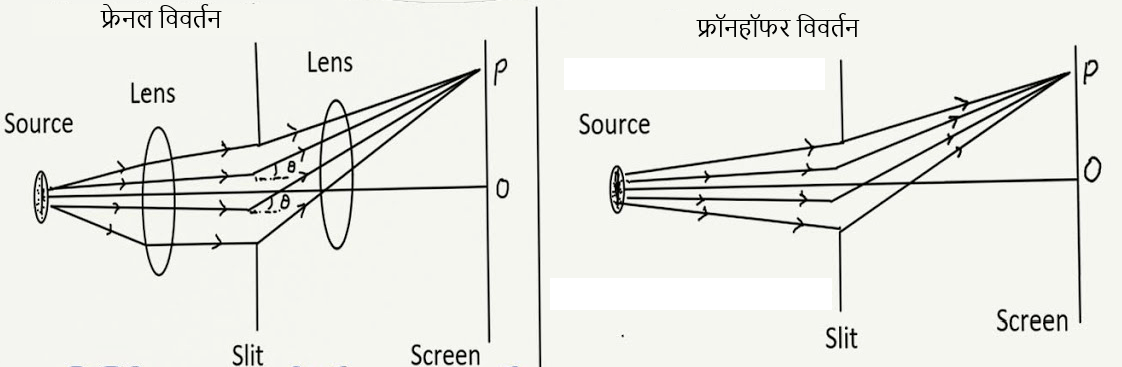
एकल छिद्र द्वारा प्रकाश का विवर्तन

जब प्रकाश को हम एकल छिद्र से गुजारते है तो पर्दे पर हमें विवर्तन की घटना स्पष्ट रूप से दिखाई देती है । जब हम ध्यान से देखते है तो ज्यामितीय छाया एक प्रकार का विवर्तन प्रतिरूप की भांति दिखाई पड़ता है । बीच में एक चौड़ी दीप्त पट्टी प्राप्त होती है जिसके दोनों ओर एकान्तर क्रम में अदीप्त तथा दीप्त फिंजे प्राप्त होती है । दीप्त फ़्रिंजो की चौड़ाई तथा तीव्रता क्रमशः घटती चली जाती है तथा अदीप्त फ़्रिंजो की चौड़ाई बढ़ती चली जाती है ।

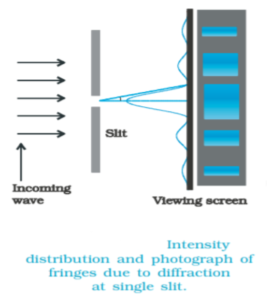
इसको समझने के लिए

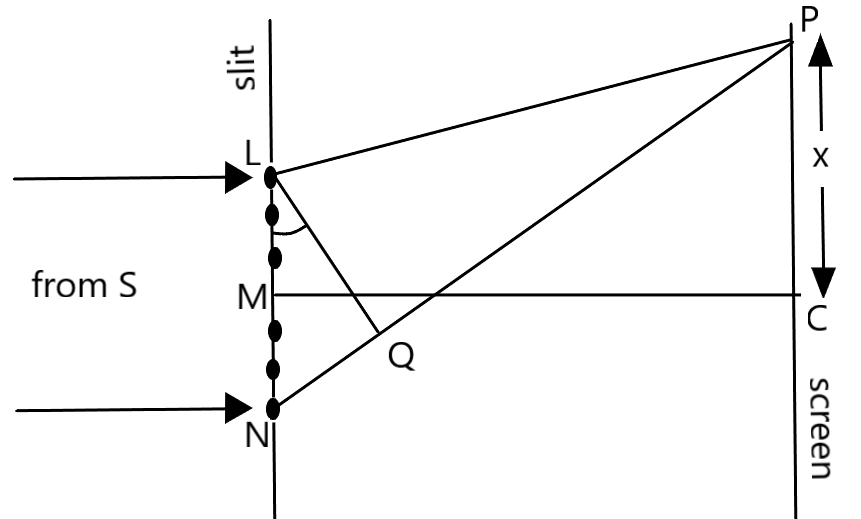
माना की एक समतल तरंगाग्र एक पतले स्लिट LN पर लम्बवत आपतित होती है । माना की स्लिट की चौड़ाई d है ।

हाइगेन्स के अनुसार स्लिट LN का प्रत्येक बिंदु , द्वितीयक तरंगिकाओं के लिए स्रोत का काम करती है । स्लिट से निकला द्वितीयक तरंगिकाएँ , पर्दे पर अध्यारोपित होती है । माना की LN का मध्य बिंदु M है ।

केंद्रीय उच्चिष्ठ

चित्र के अनुसार सभी द्वितीयक तरंगिकाएँ बिंदु C पर समान कला में अध्यारोपित होती है तथा केंद्रीय दीप्त फ्रिंज़ का निर्माण करती है । इस फ्रिंज़ को मुख्य या केंद्रीय उच्चिष्ठ कहते है ।

अब प्रकाश θ कोण पर विवर्तित हो जाता है , इस कारण से द्वितीयक तरंगिकाएँ θ कोण पर विवर्तित हो जाती है । ये तरंगिकाएँ पर्दे पर बिंदु P पर मिलती है । बिंदु P का अधिकतम तथा न्यूनतम तीव्रता पर होना द्वितीयक तरंगिकाओं के पथांतर पर निर्भर करता है ।

चित्र के अनुसार , NQ पथांतर है ।

अर्थात NP-LP=NQ=dsinθ

यदि θ बहुत ही छोटा है तो पथांतर NQ=d θ

निमनिष्ठ की स्थिति (Position for Seccondary Minima)

यदि बिंदु L तथा N का पथांतर λ जो प्रकाश के तरंगदैर्घ्य के बराबर है , हो तब बिंदु P न्यूनतम तीव्रता पर होगा । इसे बहुत ही आसानी से सिद्ध किया जा सकता है ।

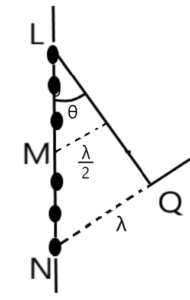
स्लिट LN के दो बराबर भाग LM तथा MN पर विचार करते है जैसा की चित्र में दिखाया गया है । यहाँ पर L तथा M से उत्पन्न द्वितीयक तरंगिकाओं के बीच पथांतर $\fn_cm \frac{\lambda}{2}$ होगा, उसी प्रकार M तथा N के बीच पथांतर $\fn_cm \frac{\lambda}{2}$ होगा ।

अर्थात हम यह कह सकते है की LM तथा MN के प्रत्येक अर्धभाग के सभी संगत बिंदुओं से चलने वाली द्वितीयक तरंगिकाओं के बीच पथांतर $\fn_cm \frac{\lambda}{2}$ होगा ।

अतः P बिंदु पर द्वितीयक तरंगिकाओं का विनाशी व्यतिकरण होगा तथा प्रथम अदीप्त फ्रिंज़ का निर्माण होगा । यह विवर्तन प्रतिरूप का प्रथम निमनिष्ठ है ।

अर्थात NQ=λ

1st निमनिष्ठ के लिए

$\fn_cm d\;sin\theta_1=\lambda$

2nd निमनिष्ठ के लिए

$\fn_cm d\;sin\theta_2=2\lambda$

………………..

…………………..

n वे निमनिष्ठ के लिए

$\fn_cm \left [ d\;sin\theta_n=\pm n\lambda \right ]\;\;\;\;\;\Rightarrow \;\;\;\;\;\left [ \theta_n=\pm \frac{n\lambda}{d} \right ]$ जहाँ n= 1,2,3……..

उच्चिष्ठ की स्थिति (Position for Seccondary Maxima)

यदि बिंदु L तथा N का पथांतर $\fn_cm \frac{3\lambda}{2}$ हो , तब बिंदु P पर 1st उच्चिष्ठ की स्थिति होगी । इसे भी बहुत आसानी से सिद्ध किया जा सकता है ।

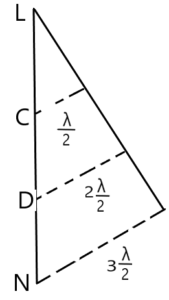
यहाँ पर स्लिट LN को तीन बराबर भाग LC , CD , तथा DN पर विचार करते है । चित्र के अनुसार LC तथा CD के सभी संगत बिंदुओं से चलने वाली द्वितीयक तरंगिकाओं के बीच पथांतर $\fn_cm \frac{\lambda}{2}$ होगा । अतः LC तथा CD भाग के लिए P बिंदु पर विनाशी अध्यारोपण होगा , लेकिन सिर्फ DN भाग से निकला द्वितीयक तरंगिकाओं के कारण जब P बिंदु पर अध्यारोपण होता है तो उससे बहुत ही कम तीव्रता का दीप्त फ्रिंज़ प्राप्त होता है । जिसे 1st उच्चिष्ठ की स्थिति कहते है ।

अर्थात NQ= $\fn_cm \frac{3\lambda}{2}$

1st उच्चिष्ठ के लिए

$\fn_cm d\;sin\theta_1^{'}=\frac{3\lambda}{2}$

2nd उच्चिष्ठ के लिए

$\fn_cm d\;sin\theta_2^{'}=\frac{5\lambda}{2}$

———————

—————–

n वे उच्चिष्ठ के लिए

$\fn_cm \left [ d\;sin\theta_n^{'}=\pm \frac{(2n+1)\lambda}{2} \right ]\;\;\;\;\;\Rightarrow \;\;\;\;\;\left [ \theta_n^{'}=\pm \frac{(2n+1)\lambda}{2d} \right ]$ जहाँ n=1,2,3………

विवर्तन में प्रकाश की तीव्रता का वितरण

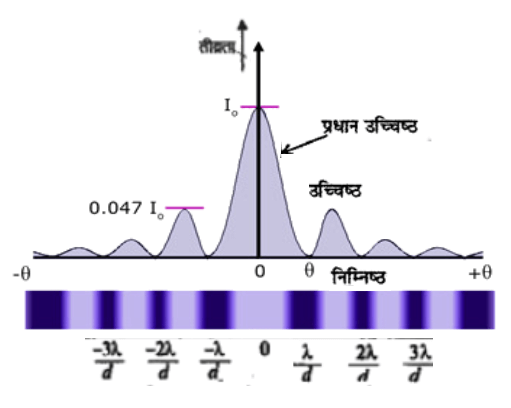
निमनिष्ठ की स्थिति के लिए

$\fn_cm \left [ d\;sin\theta_n=\pm n\lambda \right ]\;\;\;\;\;\Rightarrow \;\;\;\;\;\left [ \theta_n=\pm \frac{n\lambda}{d} \right ]$ जहाँ n= 1,2,3……..

उच्चिष्ठ की स्थिति के लिए

$\fn_cm \left [ d\;sin\theta_n^{'}=\pm \frac{(2n+1)\lambda}{2} \right ]\;\;\;\;\;\Rightarrow \;\;\;\;\;\left [ \theta_n^{'}=\pm \frac{(2n+1)\lambda}{2d} \right ]$ जहाँ n=1,2,3………

NOTE:

उच्चिष्ठ की तीव्रता केंद्र से दुरी के साथ तेजी से घटती जाती है ।
केंद्रीय उच्चिष्ठ की चौड़ाई , 1st उच्चिष्ठ की चौड़ाई के दोगुने से भी अधिक होती है ।
1st उच्चिष्ठ की तीव्रता , केंद्रीय उच्चिष्ठ की तीव्रता का 5% से भी कम होता है ।
श्वेत प्रकाश के लिए , केंद्रीय उच्चिष्ठ फ्रिंज़ श्वेत होता है लेकिन बाकि फ्रिंज़ रंगीन होता है ।

व्यतिकरण तथा विवर्तन में अंतर

व्यतिकरण

यह घटना दो कला सम्बद्ध स्रोतों से चलने वाले दो अलग अलग तरंगाग्र के बीच अध्यारोपण का परिणाम है ।
इसमें सभी दीप्त फ्रिंजे एकसमान तीव्रता की होती है ।
इसमें सभी फ्रिंजे समान चौड़ाई की होती है ।
इसमें निमनिष्ठ प्रायः पूर्णतः अंधकारमय होते है ।

विवर्तन

यह घटना एक ही तरंगाग्र के विभिन्न बिंदुओं से चलने वाली द्वितीयक तरंगिकाओं के बीच अध्यारोपण का परिणाम है ।
इसमें सभी दीप्त फ्रिंजे एकसमान नहीं होती है तथा तीव्रता घटते क्रम में होती है ।
इसमें सभी फ्रिंजे समान चौड़ाई की नहीं होती है ।
इसमें ऐसा नहीं होता है ।

केंद्रीय उच्चिष्ठ की चौड़ाई तथा कोणीय चौड़ाई

केंद्रीय उच्चिष्ठ की चौड़ाई , केंद्रीय उच्चिष्ठ के दोनों ओर 1st निमनिष्ठों के बीच की रेखीय दुरी को कहते है ।

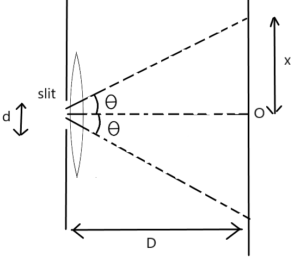
माना की लेंस, स्लिट के बहुत ही निकट है । अर्थात $\fn_cm f=D$

1st निमनिष्ठ के लिए

$\fn_cm sin\theta=\frac{\lambda}{d}-----(1)$

यदि $\fn_cm \theta$ बहुत ही छोटा हो तो

$\fn_cm sin\theta\approx \frac{x}{D}=\frac{x}{f}-----(2)$

समीकरण (1) तथा (2) से

$\fn_cm \frac{x}{f}=\frac{\lambda}{d}$

$\fn_cm \therefore \left [ x=\frac{f\lambda}{d} \right ]$

केंद्रीय उच्चिष्ठ की चैड़ाई = $\fn_cm 2x=\frac{2f\lambda}{d}=\frac{2D\lambda}{d}$

NOTE:

केंद्रीय उच्चिष्ठ की चौड़ाई, प्रकाश के तरंगदैर्घ्य के समानुपाती होती है । अर्थात लाल रंग के लिए चौड़ाई अधिक तथा बैगनी रंग के लिए चौड़ाई कम होती है ।
केंद्रीय उच्चिष्ठ की चौड़ाई स्लिट की चौड़ाई के व्युत्क्रमानुपाती होती है ।
केंद्रीय उच्चिष्ठ की चौड़ाई, स्लिट तथा पर्दे के बीच की चौड़ाई के समानुपाती होती है ।

केंद्रीय उच्चिष्ठ की कोणीय चौड़ाई = $\fn_cm 2\theta$

हम जानते है की $\fn_cm sin\theta=\frac{\lambda}{d}$

यदि $\fn_cm \theta$ बहुत ही छोटा हो तो $\fn_cm \theta=\frac{\lambda}{d}$

∴ कोणीय चौड़ाई $\fn_cm =\frac{2\lambda}{d}$

यदि $\fn_cm d>>\lambda$ , तब कोणीय चौड़ाई $\fn_cm \approx 0$

अर्थात इस स्थिति में लगभग किसी भी प्रकार का विवर्तन नहीं हुआ , जो की प्रकाश का सरल रेखा को दर्शाती है ।

NOTE:

एक वृत्तीय छिद्र वृत्तीय विवर्तन फ्रिंजे बनाता है , इस स्थिति में केंद्रीय दीप्त बैंड तथा प्रथम अदीप्त बैंड के बीच की कोणीय दुरी होती है ।

$\fn_cm \theta=\frac{1.22 \lambda}{d}$ जहाँ $\fn_cm d\rightarrow$ छिद्र का व्यास है , तथा दोनों ओर के अदीप्त बैंडों के बीच की कोणीय दुरी $\fn_cm =2\theta$ होगी ।

आंकिक प्रश्न

(1) 5500 Å तरंगदैर्घ्य का प्रकाश $\fn_cm 2.20\times 10^{-4} \;cm$ चौड़े रेखा छिद्र पर अभिलम्बवत आपतित होता है । केंद्रीय उच्चिष्ठ के दोनों ओर प्रथम दो निमनिष्ठों की कोणीय स्थितियों की गणना करें । (±0.25 रेडियन )

(2) एक दूर स्थित स्रोत से 6500 Å का प्रकाश 0.50 मिमी चौड़ी झिरी पर आपतित होता है (a) झिरी से 1.8 मीटर दूर स्थित परदे पर प्रेक्षित विवर्तन प्रारूप के केंद्रीय प्रदीप्त बैंड के दोनों ओर के अदीप्त बैंडों के बीच की दुरी क्या है ? (b) यदि झिरी को एक 0.50 मिमी व्यास के छिद्र से प्रतिस्थापित कर दिया जाये , तो उत्तर क्या होगा ? $\fn_cm (4.68\times10^{-3}m,\; 5.71\times10^{-3}m)$

(3) 0.02 सेमी चौड़ी एक झिरी पर $\fn_cm 5\times10^{-5} cm$ तरंगदैर्घ्य का प्रकाश अभिलम्बवत डाला जाता है । झिरी के ठीक पीछे 60 cm फोकस दुरी का एक उत्तल लेंस रखने पर लेंस से 60 सेमी दूर रखे परदे पर विवर्तन प्रतिरूप किया जाता है । परदे पर केंद्रीय उच्चिष्ठ तथा प्रथम अदीप्त बैंड के बीच की दुरी ज्ञात कीजिये । (0.15 cm)

(4) किसी रेखाछिद्र जिसकी चौड़ाई ‘a’ है , को 6000Å तरंगदैर्घ्य के प्रकाश द्वारा प्रकाशित किया जाता है ।’a’ के किस मान के लिए (a) प्रथम उच्चिष्ठ का विवर्तन कोण 30° प्राप्त होगा । (b) प्रथम निमनिष्ठ का कोण विवर्तन कोण 30° प्राप्त होगा ? $\fn_cm \left ( 1.8\times10^{-6}m, 1.2\times10^{-6}m \right )$

(5) किसी लेजर को $\fn_cm 5\times10^{14}Hz$ आवृत्ति पर प्रयुक्त किया जाता है जिसका द्वारक $\fn_cm 10^{-2}m$ है । कोणीय विस्तार क्या होगा ? $\fn_cm \left ( 0.6\times10^{-4}radian \right )$

(6) 0.2 mm चौड़े एक रेखा छिद्र से 2 मीटर दूर रखे परदे पर विवर्तन प्रारूप बनाया जाता है । परदे पर केंद्रीय उच्चिष्ठ के दोनों ओर 5 mm पर प्रथम निमनिष्ठ प्राप्त होता है । प्राकाः की तरंगदैर्घ्य की परिकलन कीजिये । (5000 Å)

(7)5900 Å तरंगदैर्घ्य का एकवर्णी प्रकाश $\fn_cm 11.8\times10^{-7}m$ चौड़ी एक झिरी पर अभिलम्बवत डाला जाता है तथा विवर्तन प्रारूप एक परदे पर प्राप्त किया जाता है । (a) प्रथम निमनिष्ठ (b) केंद्रीय उच्चिष्ठ की कोणीय चौड़ाई ज्ञात करें । (30°, 60°)

(8) $\fn_cm 2\times10^{-6}m$ चौड़ी एक झिरी से 590 nm तथा 596 nm तरंगदैर्घ्यों के सोडियम के प्रकाश से एक – एक करके विवर्तन प्रारूप प्राप्त किये जाते है । परदे की झिरी से दुरी 1.5 मीटर है । दोनों स्थितियों में विवर्तन प्रारूपों के प्रथम उच्छिष्ठों के बीच की दुरी ज्ञात कीजिये । ( 6.75 mm)

एकल स्लिट विवर्तन पैटर्न का अवलोकन

प्रकाश यंत्रों की विभेदन क्षमता ( Resolving Power of Otical Instruments)

जब किसी बिन्दुवत वस्तु से चलने वाला प्रकाश किसी प्रकाशिक यंत्र में से गुजरता है , तो उस वस्तु का प्रतिबिम्ब ठीक बिन्दुवत प्राप्त नहीं होता है , जबकि एक चकती या धब्बा सा प्राप्त होता है जिसे विवर्तन चित्र (Diffraction Pattern) कहते है । ऐसा प्रकाश की तरंग प्रकृति के कारण होता है ।

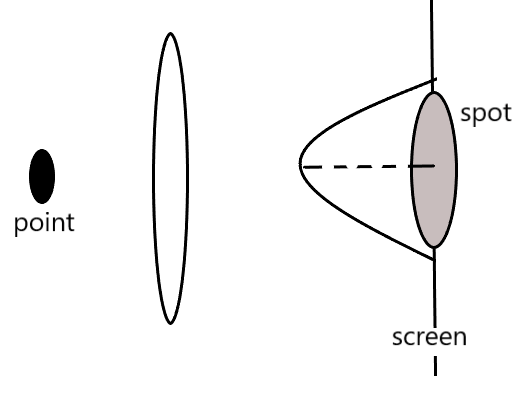
यदि दो बिन्दुवत वस्तुएँ एक दूसरे के बहुत समीप स्थित हो तो प्रकाशिक यंत्र द्वारा उनके विवर्तन चित्र भी एक दूसरे के समीप बनते है जिससे उनमे अतिव्यापन (Overlapping) होता है ।

जब इन विवर्तन चित्रों में अतिव्यापन कम होता है , तब प्रकाशिक यंत्र में दोनों वस्तुएं अलग अलग दिखाई देती है , अर्थात प्रकाशिक यंत्र दोनों वस्तुओं में विभेद (Resolve) करने में समर्थ होता है । लेकिन जब इन विवर्तन चित्रों में अतिव्यापन अधिक होता है , तब प्रकाशिक यंत्र उनमे विभेद नहीं कर पाता है ।

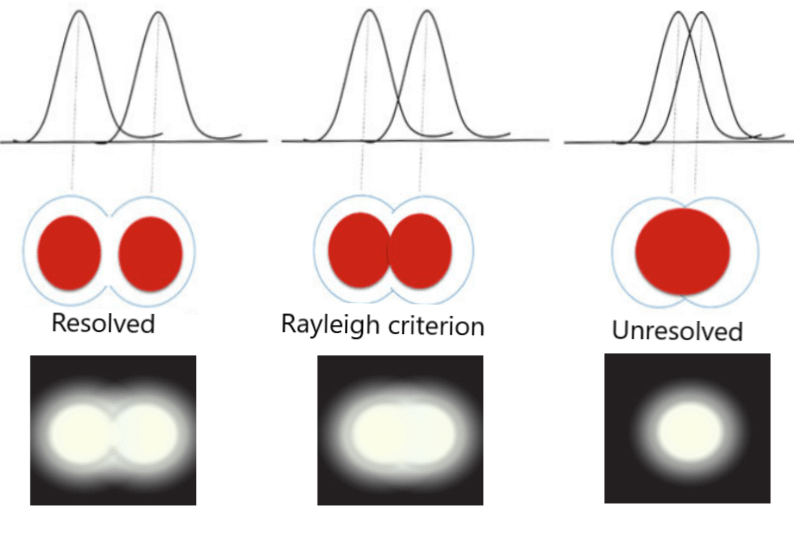
किसी प्रकाशिक यंत्र द्वारा दो पास – पास स्थित वस्तुओं के अलग अलग स्पष्ट प्रतिबिम्ब बनाने की क्षमता को उसकी विभेदन क्षमता कहते है । दो वस्तुओं के बीच की वह न्यूनतम दुरी जब वे वस्तुएं किसी प्रकाशिक यंत्र द्वारा अलग अलग दिखाई देती है , उस प्रकाशिक यंत्र की विभेदन क्षमता सीमा कहते है ।

प्रकाशिक यंत्र की विभेदन सीमा जितनी कम होती है , उसकी विभेदन क्षमता उतनी ही अधिक होती है ।

अर्थात

NOTE:- मानव नेत्र के लिए विभेदन सीमा 1′ या 1/60 degree होता है ।

रैले (Rayleigh) के अनुसार दो वस्तु या बिंदु भाग विभेदित (Just Resolved) होते है , यदि प्रथम वस्तु के बिम्ब का केंद्रीय उच्चिष्ठ दूसरी वस्तु के बिम्ब का निमनिष्ठ का अध्यारोपण करती है

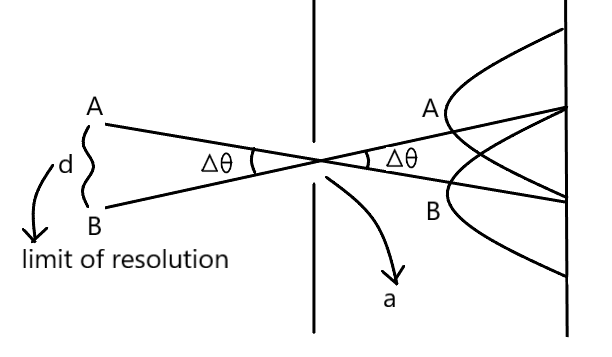
विवर्तन प्रभाव के कारण एक गोलीय लेंस ( वृताकार द्वारक ) द्वारा एक बिन्दुवत वस्तु का प्रतिबिम्ब वास्तव में एक दीप्त वृताकार केंद्रीय क्षेत्र होता है , जो अदीप्त तथा दीप्त वलयों से घिरा होता है ।

ऐसा पाया गया है की वृतारकर द्वारक के लिए , विभेदन सीमा

$\fn_cm \left [\Delta \theta=\frac{1.22 \lambda}{a} \right ]$ slit के लिए $\fn_cm \Delta\theta=\frac{2\lambda}{a}$

जहाँ $\fn_cm \lambda\rightarrow$ प्रयुक्त प्रकाश का तरंगदैर्घ्य है

$\fn_cm a\rightarrow$ द्वारक की चौड़ाई है

दूरदर्शी की विभेदन क्षमता (Resolving Power of Telescope)

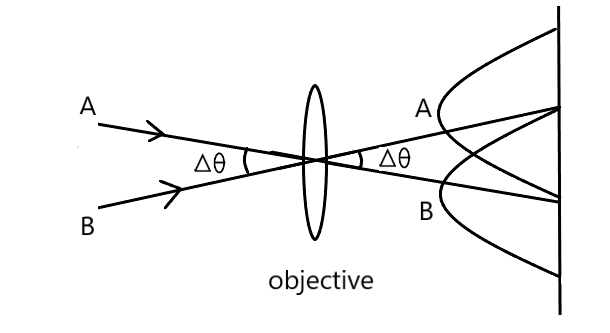
दूरदर्शी द्वारा, दूर स्थित दो पास पास वस्तुओं के अलग अलग स्पष्ट प्रतिबिम्ब बनाने की क्षमता को दूरदर्शी की विभेदन क्षमता कहते है । हम जानते है की वृताकार द्वारक के लिए विभेदन क्षमता होती है

$\fn_cm \Delta\theta=\frac{1.22\lambda}{a}$ जहाँ $\fn_cm a\rightarrow$ अभिदृश्यक (Objective) लेंस के द्वारक की चौड़ाई है ।

∴ दूरदर्शी का विभेदन क्षमता = $\fn_cm = \frac{1}{\Delta \theta}$

$diffraction$

यदि a का आकार बड़ा तथा λ छोटा हो तो विभेदन क्षमता अधिक होगा । चूँकि दूरदर्शी से दूर की वस्तुएं देखी जाती है जो सूर्य के प्रकाश से ही प्रकाशित होती है । अतः दूरदर्शी के लिए λ पर हमारा नियंत्रण नहीं होता है ।

स्पष्ट है की दूरदर्शी का अभिदृश्यक बड़े द्वारक का होना चाहिए ।

सूक्ष्मदर्शी का विभेदन क्षमता

सूक्षमदर्शी की विभेदन क्षमता निकट में एक दूसरे के करीब स्थित दो बिंदु वस्तुओं के प्रतिबिम्बों को अलग अलग दिखने की क्षमता है ।

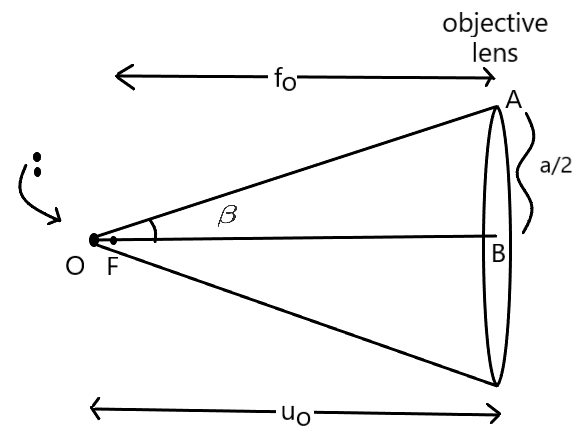
यहाँ पर दो बिंदु वस्तुओं को अभिदृश्यक (Objective) लेंस के फोकस से कुछ ही अधिक दुरी पर रखी जाती है , ताकि उसका वास्तविक तथा बड़ा प्रतिबिम्ब बन सके ।

अर्थात , $diffraction$

छोटे द्वारक के लिए , हम लिख सकते है

$diffraction$

$diffraction of light$

जहाँ $\fn_cm a\rightarrow$ द्वारक की चौड़ाई है ।

अब

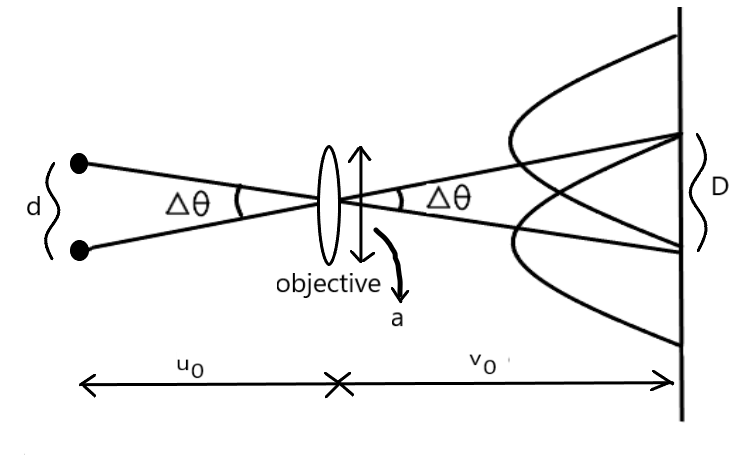
चित्र के अनुसार , $diffraction of light$

हम जानते है की ,

$diffraction of light$

उसी प्रकार , लेंस की आवर्धन क्षमता होगी ,

$diffraction of light$

समीकरण (1) और (2) से

$diffraction of light$

$\fn_cm \therefore \;\;d$ ( विभेदन सीमा ) $\fn_cm =\frac{1.22 \lambda}{2 \sin\beta}$

अतः सूक्ष्मदर्शी का विभेदन क्षमता होगी

$diffraction of light$

यदि वस्तु तथा अभिदृश्यक लेंस के बीच वायु न होकर μ अपवर्तनांक का कोई माध्यम हो , तो सूक्ष्मदर्शी का विभेदन क्षमता होगी

$diffraction of light$

सूक्ष्मदर्शी की विभेदन क्षमता बढ़ाने के लिए —

$\fn_cm \beta$ का मान अधिक रखना पड़ेगा , यह तभी संभव है जब छोटी फोकस दुरी के लेंस का उपयोग किया जाये क्योंकि बड़े द्वारक वाले अभिदृश्यक को उपयोग में लाना संभव नहीं है ।
उच्च अपवर्तनांक वाले माध्यम का प्रयोग किया जाना चाहिए तथा
छोटी तरंगदैर्घ्य ( बैगनी रंग ) का प्रकाश प्रयुक्त करना चाहिए ।

NOTE:- दूरदर्शी का मुख्य गुण है विभेदन क्षमता तथा सूक्ष्मदर्शी का मुख्य गुण है आवर्धन

आंकिक प्रश्न

(1) तरंगदैर्घ्य 0.6μm पर 10 सेमी व्यास वाले एक दूरदर्शी का कोणीय विभेदन क्या होगा । ( $\fn_cm (6\times10^{-6} rad)$

(2) एक खगोलीय दूरदर्शी के अभिदृश्यक का व्यास 6 cm है । 540 nm तरंगदैर्घ्य का प्रकाश प्रयुक्त करने पर इसकी विभेदन क्षमता कितनी होगी ? $\fn_cm (9.11\times10^4)$

किरण प्रकाशिकी की वैधता ( फ्रेनल दुरी ) Validity of Ray Optics ( Fresnal Distance)

किरण प्रकाशिकी इस अवधारणा पर आधारित है की प्रकाश सीधी रेखा में गमन करती है लेकिन तरंग प्रकाशिकी ( विशेष रूप से विवर्तन प्रभाव ) इस अवधारणा पर आधारित है की प्रकाश सीधी रेखा में गमन नहीं करती है , यह किनारों पर मुड़ती है

फ्रेनल दुरी को पर्दे तथा रेखा छिद्र के बीच की दुरी के रूप में व्यक्त किया जाता है , जब प्रकाश के विवर्तन के कारण प्राप्त प्रकाश का केंद्र से फैलाव रेखा छिद्र के आकार ( चौड़ाई ) के बराबर हो जाता है । इसे $\fn_cm Z_F$ द्वारा सूचित किया जाता है ।

हम जानते है की केंद्रीय उच्चिष्ठ की चौड़ाई केंद्र से होती है

$diffraction of light$

जब $\fn_cm x=d$ तब $\fn_cm D=Z_F$ ( फ्रेनल दुरी )

$diffraction of light$

यदि $diffraction of light$ , तब विवर्तन के प्रभाव को नज़र अंदाज़ तथा किरण प्रकाशिकी को वैध माना जा सकता है । . यदि $diffraction of light$ , तब विवर्तन को नज़र अंदाज़ नहीं किया जा सकता है तथा उस स्थिति में किरण प्रकाशिकी को वैध नहीं माना जा सकता है ।

आंकिक प्रश्न

(1) उस दुरी का आँकलन कीजिये जिसके लिए एक 4 मिमी आकार की वस्तु द्वारा तथा 400 nm तरंगदैर्घ्य के प्रकाश के लिए किरण प्रकाशिकी सन्निकट रूप से लागु होती है । ( 40 मीटर )

(2) वह दुरी ज्ञात कीजिये जिसके लिए 3 mm चौड़ाई के द्वारक द्वारा तथा 500 nm तरंगदैर्घ्य के प्रकाश के लिए किरण प्रकाशिकी सन्निकट रूप से लागु होती है । (18 मीटर )

(3) जब किसी प्रकाश पुंज जिसकी तरंगदैर्घ्य 500 nm है, जो बिना किसी विशेष विस्तार के गति कर सकता है , यदि द्वारक 3 mm चौड़ाई का हो तो प्रकाश पुंज द्वारा तय दुरी की गणना कीजिये । ( 18 m)

(4) $\fn_cm 5\times10^{-7}m$ तरंगदैर्घ्य का प्रकाश $\fn_cm 2\times10^{-3}m$ चौड़ाई के द्वारक द्वारा विवर्तित किया जाता है । विवर्तित प्रकाश पुंज की किस तय दुरी के लिए विवर्तन का फैलाव द्वारक के आकार से अधिक हो जाता है ? ( 8m)

(5) 600 nm तरंगदैर्घ्य का प्रकाश किसी 2 nm आकार वाले द्वारक पर आपतित होता है । वह दुरी ज्ञात कीजिये जहाँ तक प्रकाश किरणें इस प्रकार गति कर सकती है , की इसका फैलाव द्वारक के आकार की तुलना में कम हो । (6.7 m)

(6) दो पहाड़ियों पर दो मीनारें परस्पर 40 km की दुरी पर है । इन्हे जोड़ने वाली रेखा इनके मध्य में पड़ने वाली किसी पहाड़ी के 50 मीटर ऊपर से गुजरती है । उन रेडियो तरंगों की अधिकतम तरंगदैर्घ्य ज्ञात कीजिये जो मीनारों के मध्य बिना अवगम्य विवर्तन प्रभाव के भेजी जा सके । $\fn_cm (12.5\times10^{-2}m)$

प्रश्न

(1) प्रकाश के विवर्तन से आप क्या समझते है ?

(2) एकल रेखा छिद्र से प्रथम निमनिष्ठ प्राप्त करने की क्या शर्त है ?

(3) लम्बी दुरी के संचार के लिए सूक्ष्म तरंगों का उपयोग क्यों किया जाता है ?

(4) फ्रेनेल दुरी क्या है ?

(5) किसी प्रकाशिक उपकरण की विभेदन क्षमता / विभेदन सीमा के बारे में बतलाइये ।

(6) संयुक्त सूक्ष्मदर्शी की विभेदन क्षमता से क्या तात्पर्य है ? इसे किस प्रकार बढ़ाया जा सकता है ।

(7) दूरदर्शी की विभेदन क्षमता से क्या तात्पर्य है ? इसे किस प्रकार बढ़ाया जा सकता है ।

(8) हम एक खुली दीवार के दूसरी ओर खड़े दोस्त को सुन सकते है, परन्तु देख नहीं सकते । समझाइये क्यों ?

(9) जब हम आधी बंद की हुई आँखों से किसी प्रबल प्रकाश स्रोत को देखते है तो प्रकाश की पत्तियां दिखाई देती है । समझाइये ।

(10) दो निकट तथा संकरे रेखा छिद्रों को एकल एकवर्णीय प्रकाश से प्रकाशित किया जाता है । परदे पर प्राप्त प्रतिरूप का नाम बतलाइये । एक रेखाछिद्र को ढँक दिया जाता है । अब परदे पर प्राप्त प्रतिरूप का नाम क्या है ? इन दोनों स्थितियों में प्राप्त प्रतिरूपों के मध्य दो अंतर लिखिए ।

(11) सूक्ष्मदर्शी की विभेदन क्षमता कैसे प्रभावित होती है जब

(a) दीप्त विकिरणों की तरंगदैर्घ्य घटती है ।
(b) अभिदृश्यक लेंस का व्यास घटता है ।

(12) खगोलीय दूरदर्शी की विभेदन क्षमता को परिभाषित करें । यह निम्न द्वारा कैसे प्रभावित होती है ।

(a) अभिदृश्यक लेंस के छिद्र के बढ़ने से
(b) प्रयुक्त प्रकाश की तरंगदैर्घ्य बढ़ने से

(13) एकल झिरी द्वारा उत्पन्न विवर्तन प्रारूप किस प्रकार प्रभावित होगा , यदि

(a) झिरी की चौड़ाई बढ़ाई जाये
(b) एकवर्णी प्रकाश के स्थान पर श्वेत प्रकाश प्रयुक्त किया जाये ।

(14) दूर स्थित स्रोत से आने वाले प्रकाश के मार्ग में एक लघु वृत्तीय वस्तु रखने पर वस्तु की छाया के मध्य में एक दीप्त बिंदु दिखाई देता है , क्यों ?

(15) फ्राउनहॉफर विवर्तन तथा फ्रेनेल विवर्तन में अंतर स्पष्ट कीजिये ।

(16) संयुक्त सूक्ष्दर्शी की विभेदन क्षमता में क्या परिवर्तन होगा , जब

(a) अभिदृश्यक लेंस तथा वस्तु के बीच के माध्यम का अपवर्तनांक बढ़ाया जाये
(b) प्रयुक्त प्रकाश की तरंगदैर्घ्य बढ़ाई जाये ।

(17) क्या विवर्तन को व्यतिकरण की एक विशिष्ट अवस्था माना जा सकता है ? कारण सहित स्पष्ट कीजिये ।

(18) एकल झिरी विवर्तन प्रतिरूप में केंद्रीय उच्चिष्ठ की कोणीय चौड़ाई किस प्रकार प्रवर्तित होगी , यदि

(a) झिरी की चौड़ाई बढ़ा दी जाये
(b) परदे तथा झिरी के बीच की दुरी बढ़ा दी जाये तथा
(c) प्रयुक्त प्रकाश की तरंगदैर्घ्य कम कर दी जाये

(19) प्रयोगशाला में एक रेखाछिद्र द्वारा प्रकाश का विवर्तन देखा जा रहा है । विवर्तन प्रतिरूप पर क्या प्रभाव पड़ेगा यदि

(a) प्रयुक्त प्रकाश की तरंगदैर्घ्य कम कर दी जाये
(b) रेखा छिद्र को कुछ और संकरा कर दिया जाये
(c) पहले रेखाछिद्र के समीप ही एक दूसरा समांतर रेखाछिद्र बना दी जाये ।

(20) यंग के प्रयोग में फ्रिंज़ की स्थति के साथ उसकी तीव्रता में परिवर्तन प्रदर्शित करने वाला ग्राफ खींचिए जबकि

(a) दोनों स्लिटें खुली हों
(b) दोनों में से एक स्लिट बंद हो

(1) प्रकाश के व्यतिकरण तथा विवर्तन में अंतर लिखिए ।

(2) एकल रेखा छिद्र विवर्तन को विस्तार से समझाइये तथा उच्चिष्ठ की रेखीय चौड़ाई के लिए सम्बन्ध प्राप्त कीजिये ।

(3) फ्रेनेल दुरी को समझाइये । इसके लिए व्यंजक ज्ञात कीजिये ।

विवर्तन के प्रकार

एकल छिद्र द्वारा प्रकाश का विवर्तन

केंद्रीय उच्चिष्ठ

निमनिष्ठ की स्थिति (Position for Seccondary Minima)

उच्चिष्ठ की स्थिति (Position for Seccondary Maxima)

विवर्तन में प्रकाश की तीव्रता का वितरण

NOTE:

व्यतिकरण तथा विवर्तन में अंतर

व्यतिकरण

विवर्तन

केंद्रीय उच्चिष्ठ की चौड़ाई तथा कोणीय चौड़ाई

NOTE:

NOTE:

आंकिक प्रश्न

एकल स्लिट विवर्तन पैटर्न का अवलोकन

प्रकाश यंत्रों की विभेदन क्षमता ( Resolving Power of Otical Instruments)

दूरदर्शी की विभेदन क्षमता (Resolving Power of Telescope)

सूक्ष्मदर्शी का विभेदन क्षमता

आंकिक प्रश्न

किरण प्रकाशिकी की वैधता ( फ्रेनल दुरी ) Validity of Ray Optics ( Fresnal Distance)

आंकिक प्रश्न

प्रश्न

विद्यार्थी NCERT के प्रश्नों को भी हल करें