गोलीय पृष्ठों पर अपवर्तन तथा लेंस -

विषय :- गोलीय पृष्ठों से अपवर्तन , पतले गोलीय लेंस, लेंस निर्मात्री सूत्र, लेंस , आवर्धन , लेंस की क्षमता , लेंसों का संयोग

◊ गोलीय अपवर्तक सतह

गोलीय अपवर्तक सतह एक ऐसा अपवर्तक माध्यम है जिसकी वक्र सतह किसी गोले का एक भाग होती है । गोलीय अपवर्तक सतह दो प्रकार की होती है ।

(1) उत्तल गोलीय अपवर्तक सतह :- जिसका विरल माध्यम की ओर सतह उत्तल ( उठा हुआ ) हो ।

(2) अवतल गोलीय अपवर्तक सतह :- जिसका विरल माध्यम की ओर सतह अवतल ( धंसा हुआ ) हो ।

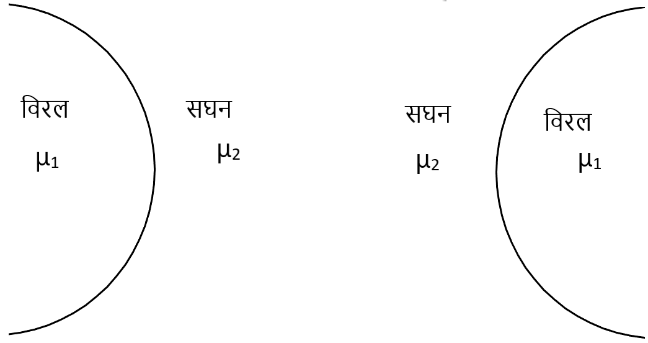
◊ उत्तल गोलीय सतह द्वारा अपवर्तन जबकि वस्तु विरल माध्यम में स्थित हो

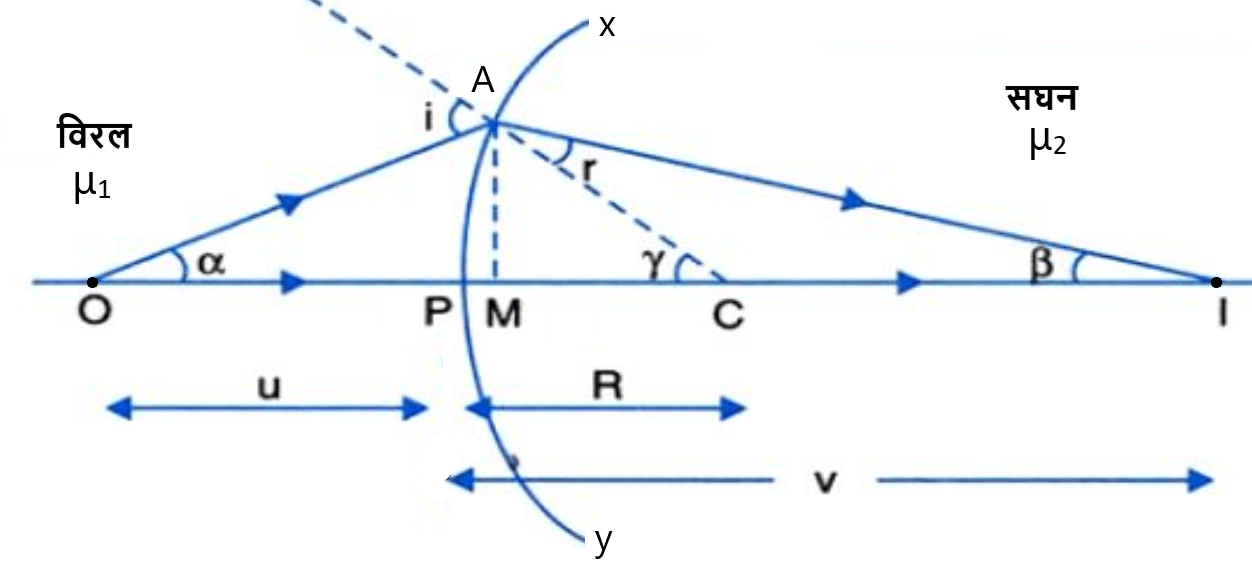
माना की XY एक उत्तल गोलीय अपवर्तक सतह है जो विरल माध्यम को सघन माध्यम से अलग करती है

माना P – सतह का ध्रुव है
C – वक्रता केंद्र है

माना O एक बिन्दुवत वस्तु है जो मुख्य अक्ष पर विरल माध्यम में स्थित है । जिसका अपवर्तन के बाद एक वास्तविक प्रतिबिम्ब I सघन माध्यम में बनता है जैसा की चित्र में दिखाया गया है । AN जो मुख्य अक्ष पर लम्ब खिंचा गया है ।

Let $\fn_cm \angle AOM=\alpha , \angle AIM=\beta , and \angle ACM=\gamma$

चित्र के अनुसार, $\fn_cm \tan \alpha =\frac{AM}{MO}$

यदि $\fn_cm \alpha$ बहुत छोटा है ( उपाक्षीय किरण के लिए )

$\fn_cm \large \tan \alpha \approx \alpha$

$\fn_cm \therefore \alpha =\frac{AM}{MO}-----(a)$

उसी प्रकार ,

$\fn_cm \beta =\frac{AM}{MI}-----(b)$

$\fn_cm \gamma =\frac{AM}{MC}-----(c)$

हम जानते है की किसी त्रिभुज के लिए बाह्य कोण सामने के दो अन्तः कोणों के योग के बराबर होती है ।

अर्थात $\fn_cm \Delta AOC$ में

$\fn_cm \large i=\alpha +\gamma -----(1)$

और $\fn_cm \Delta AIC,$ से

$\fn_cm \large \gamma =r+\beta$

$\fn_cm \large r=\gamma -\beta -----(2)$

स्नेल के नियम के अनुसार ,

$\fn_cm \large \frac{\sin i}{\cos r}=\frac{\mu _{2}}{\mu _{1}}$

बहुत ही छोटे कोण के लिए , हम लिख सकते है

$\fn_cm \large \frac{i}{r}=\frac{\mu _{2}}{\mu _{1}}$

समीकरण (1) और (2) से

$\fn_cm \large \frac{\alpha +\gamma }{\gamma -\beta }=\frac{\mu _{2}}{\mu _{1}}$

समीकरण (a) ,(b) तथा (c) से

$\fn_cm \large \frac{\frac{AM}{MO}+\frac{AM}{MC}}{\frac{AM}{MC}-\frac{AM}{MI}}=\frac{\mu _{2}}{\mu _{1}}$

$\fn_cm \large \frac{\frac{1}{MO}+\frac{1}{MC}}{\frac{1}{MC}-\frac{1}{MI}}=\frac{\mu _{2}}{\mu _{1}}$

उपाक्षीय किरण के अनुसार P तथा M एक ही बिंदु पर स्थित होंगे ,

i.e $\fn_cm \large \frac{\frac{1}{PO}+\frac{1}{PC}}{\frac{1}{PC}-\frac{1}{PI}}=\frac{\mu _{2}}{\mu _{1}}$

चिन्ह परिपाटी के अनुसार

$\fn_cm PO=-u,PC=R,PI=v$

$\fn_cm \large \therefore \frac{\frac{1}{-u}+\frac{1}{R}}{\frac{1}{R}-\frac{1}{v}}=\frac{\mu _{2}}{\mu _{1}}$

$\fn_cm \large \Rightarrow -\frac{\mu _{1}}{u}+\frac{\mu _{1}}{R}=\frac{\mu _{2}}{R}+\frac{\mu _{2}}{v}$

$\fn_cm \LARGE \Rightarrow \left [\frac{\mu _{2}}{v}-\frac{\mu _{1}}{u}=\frac{\mu _{2}-\mu _{1}}{R} \right ]$

विद्यार्थी बाकि के व्यंजक खुद से बनाये , निचे मैं यहाँ सिर्फ उसका चित्र बना दे रहा हूँ ।

◊ अवतल गोलीय सतह द्वारा अपवर्तन जबकि वस्तु विरल माध्यम में स्थित हो

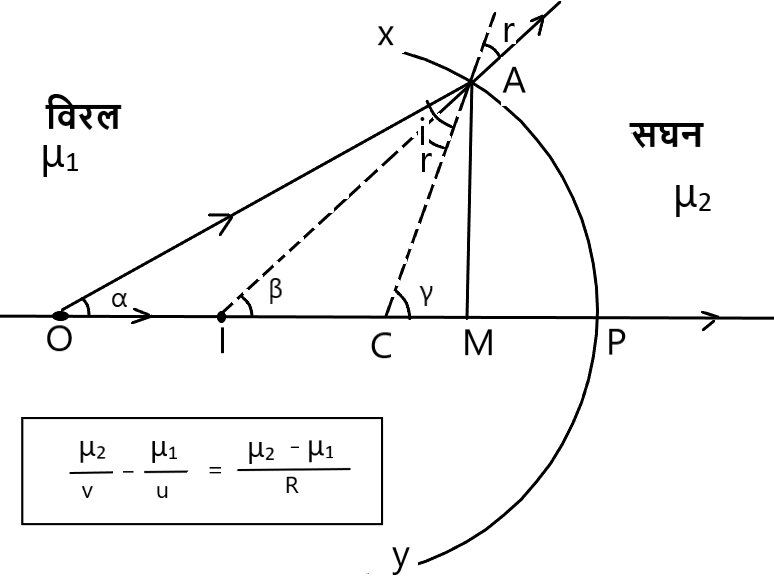
◊ उत्तल गोलीय सतह द्वारा अपवर्तन जबकि वस्तु सघन माध्यम में स्थित हो

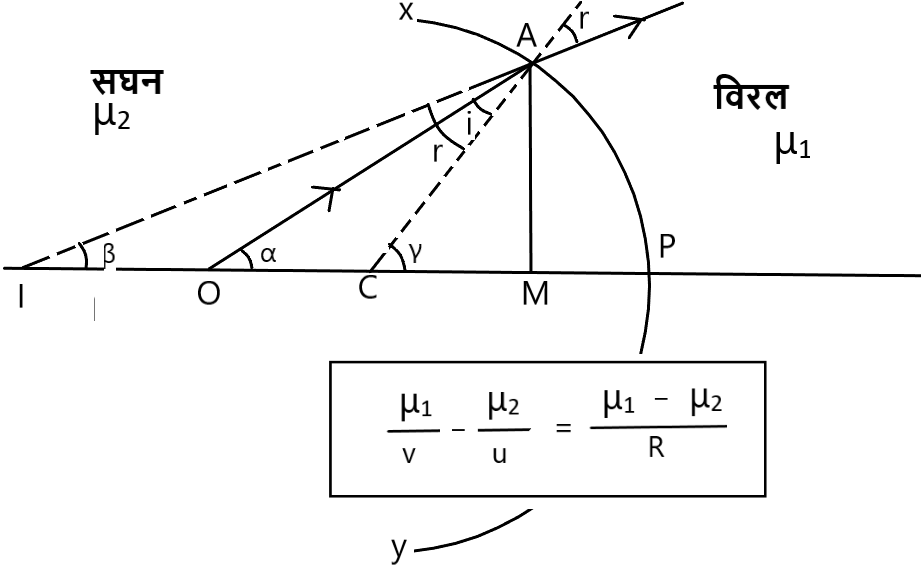
◊ अवतल गोलीय सतह द्वारा अपवर्तन जबकि वस्तु सघन माध्यम में स्थित हो

अभ्यासार्थ प्रश्न 1

(1) ऊपर के चारों condition के लिए सूत्र परीक्षा के पहलु से बहुत ही उपयोगी है , विद्यार्थी इसे बार बार दुहराएँ ।

(1) कांच के 6 सेमी व्यास के एक ठोस गोले के अंदर वायु का एक बुलबुला गोले के पृष्ठ से व्यास के अनुदिश देखने पर पास वाले पृष्ठ से 2 सेमी की दुरी पर दिखाई देता है । गोले के अंदर बुलबुले की वास्तविक स्थिति ज्ञात कीजिए । ( 2.57 सेमी )

(2) 12 सेमी त्रिज्यावाले कांच के गोले के अंदर के केंद्र से 3 सेमी की दुरी पर एक छोटा सा धब्बा है । यदि केंद्र और धब्बे को मिलाने वाली रेखा पर धब्बे के निकटतम छोर से देखा जाये , तो धब्बा कहाँ दिखाई देगा? ( सतह से 8 सेमी की दुरी पर )

(3) एक कांच की बेलनाकार छड़ के सिरे को 2 सेमी त्रिज्या के अर्धगोलीय आकार का बना दिया गया है । इस सिरे से कांच की ओर 12 सेमी की दुरी पर एक वस्तु स्थित है । वस्तु का प्रतिबिम्ब पृष्ठ से कितनी दूर बनेगा । (8 सेमी )

(4) 4 सेमी त्रिज्या के कांच के एक गोले के केंद्र से 1 सेमी की दुरी पर वायु का एक बुलबुला है । कांच का अपवर्तनांक 1.5 है । (a) बुलबुले के निकट वाले पृष्ठ से देखने पर (b) बुलबुले के दूर वाले पृष्ठ से देखने पर वह कहाँ दिखाई देगा । (2.7 सेमी, 5.71 सेमी )

◊ लेंस

लेंस किसी पारदर्शक माध्यम का एक टुकड़ा होता है जो दो अपवर्तक सतहों द्वारा घिरा हुआ होता है जिनमे से कम से कम एक सतह वक्रित होती है ।

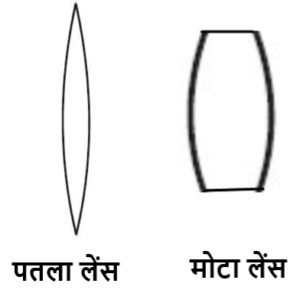
यहाँ पर हमलोग पतले लेंस की चर्चा करेंगे

लेंस दो प्रकार के होते है

(1) उत्तल लेंस :- इस लेंस का केंद्रीय भाग अपेक्षाकृत मोटा होता है । यह अभिसारी लेंस की तरह व्यवहार करता है अर्थात मुख्य अक्ष के समान्तर आती किरणों को एक बिंदु पर मिलाती है ।

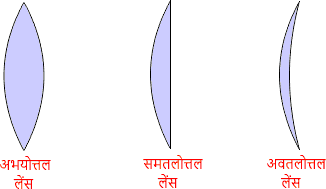
(2) अवतल लेंस :- इस लेंस का केंद्रीय भाग अपेक्षाकृत पतला होता है । यह अपसारी लेंस की तरह व्यवहार करता है अर्थात मुख्य अक्ष के समान्तर आती किरणें अपवर्तन के बाद एक बिंदु से आती हुई प्रतीत होती है ।

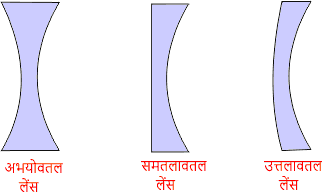
◊ लेंस से सम्बंधित महत्वपूर्ण राशि

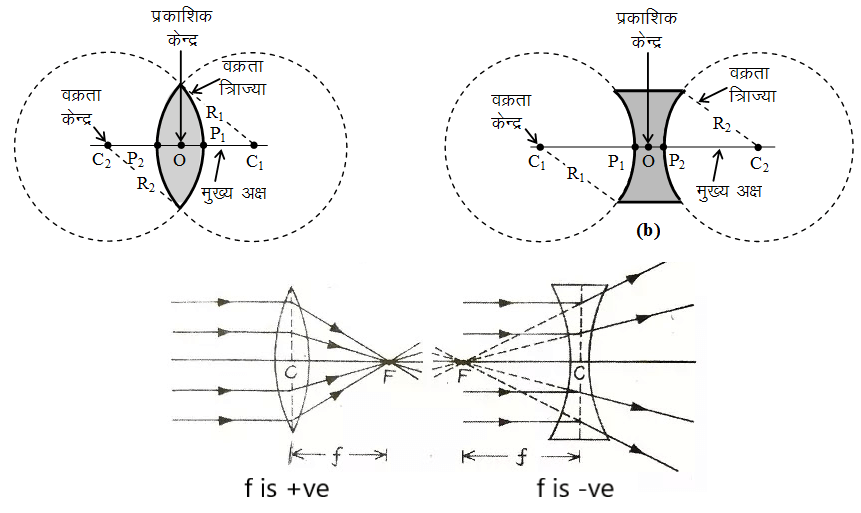
◊ लेंस निर्मात्री सूत्र

यह सूत्र लेंस की फोकस दुरी, लेंस के पदार्थ का अपवर्तनांक तथा इसके पृष्ठ की वक्रता त्रिज्याओं के मध्य सम्बन्ध को बतलाती है । लेंस बनाने वाले लोग इस समीकरण का उपयोग दी गई फोकस दुरी का लेंस बनाने में करते है ।

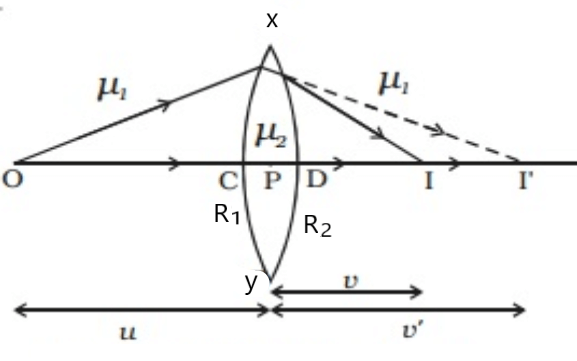
माना की XY एक पतला उत्तल लेंस है जिसका प्रकाशिक केंद्र O है । माना की $R_{1}$ तथा $R_{2}$ दोनों सतहों की वक्रता त्रिज्याएँ , $\mu _{1}$ लेंस का अपवर्तनांक तथा $\mu _{2}$ उस माध्यम का अपवर्तनांक है जिसमे लेंस रखा गया है ।

माना की O एक बिन्दुवत वस्तु है जिसे मुख्य अक्ष पर रखा गया है । पहले सतह के अपवर्तन के बाद इसका आभासी प्रतिबिम्ब I’ मुख्य अक्ष पर बनता है ।

अर्थात

$\fn_cm \large \frac{\mu _{2}}{v'}-\frac{\mu _{1}}{u}=\frac{\mu _{2}-\mu _{1}}{R_{1}}-----(1)$

(NOTE:- sign convention is not used here, because at the time of this derivation we already took sign convention)

दूसरे अपवर्तन के लिए I’ वस्तु की तरह कार्य करती है जिसका दूसरे सतह के अपवर्तन के बाद वास्तविक प्रतिबिम्ब I मुख्य अक्ष पर बनता है ।

अर्थात $\fn_cm \large \frac{\mu _{1}}{v}-\frac{\mu _{2}}{v'}=\frac{\mu _{1}-\mu _{2}}{R_{2}}-----(2)$

समीकाण (1) तथा (2) को जोड़ने पर

$\fn_cm \large \frac{\mu_2}{v^{'}}-\frac{\mu_1}{u}+\frac{\mu_1}{v}-\frac{\mu_2}{v^{'}}=\frac{\mu_2-\mu_1}{R_1}+\frac{\mu_1-\mu_2}{R_2}$

$\fn_cm \large \frac{\mu _{1}}{v}-\frac{\mu _{1}}{u}=\left ( \mu _{2}-\mu _{1} \right )\left ( \frac{1}{R_{1}}-\frac{1}{R_{2}} \right )$

$\fn_cm \large \frac{1}{v}-\frac{1}{u}=\left ( \frac{\mu _{2}}{\mu _{1}}-1 \right )\left ( \frac{1}{R_{1}}-\frac{1}{R_{2}} \right )$

$\fn_cm \large if\; u\rightarrow \infty \; ,\; then\; v\rightarrow f$

$\fn_cm \large \left [ \frac{1}{f}=\left ( \frac{\mu _{2}}{\mu _{1}}-1 \right )\left ( \frac{1}{R_{1}}-\frac{1}{R_{2}} \right ) \right ]$

यह लेंस निर्मात्री सूत्र है ।

NOTE:-

(a) लेंस की मुख्य अक्ष के समान्तर आपतित किरणें लेंस के अपवर्तन के बाद मुख्य फोकस से होकर गुजरती है ( उत्तल लेंस के लिए ) या मुख्य फोकस से आती हुई प्रतीत होती है( अवतल लेंस के लिए )

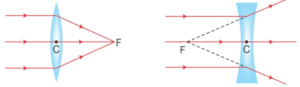
(b) लेंस के प्रकाशिक केंद्र से होकर गुजरने वाली किरणें बिना विचलित तथा विस्थापित हुए सीधी चली जाती है । ( पतले लेंस के लिए ही यह संभव है )

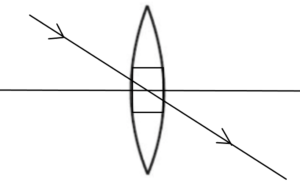
अभ्यासार्थ प्रश्न 2

(1) कांच के एक द्वी – उत्तल लेंस की वक्रता – त्रिज्याएँ क्रमश : 20 सेमी तथा 30 सेमी है । लेंस की फोकस दुरी ज्ञात करें । ( 24 सेमी )

(2) काँच के बने एक उत्तल लेंस की वक्रता त्रिज्याएँ क्रमशः 15 सेमी तथा 30 सेमी है । लेंस की फोकस दुरी ज्ञात करें । (20 सेमी )

(3) कांच के बने एक द्वी उत्तल लेंस की वक्रता त्रिज्याएँ 20 सेमी तथा 40 सेमी है । कांच का अपवर्तनांक ज्ञात करें । (1.67 )

(4) काँच के एक पतले समतलउत्तल लेंस की फोकस दुरी 40 सेमी है । लेंस के वक्र पृष्ठ की त्रिज्या ज्ञात करें । (20 सेमी )

(5) काँच के बने एक उत्तल लेंस की वक्रता त्रिज्याएँ 15 सेमी तथा 30 सेमी है । यदि कम वक्रता वाला पृष्ठ अवतल हो , तो लेंस की फोकस दुरी ज्ञात कीजिये । ( 60 सेमी )

(6) एक द्वी उत्तल लेंस की फोकस दुरी 25 सेमी है । लेंस के एक पृष्ठ की वक्रता त्रिज्या दूसरे की दोगुनी है । लेंस के दोनों पृष्ठ का वक्रता त्रिज्या ज्ञात करें । ( 18.75 सेमी , 37.5 सेमी )

(7) काँच के एक द्वी उत्तल लेंस की वक्रता त्रिज्याओं का अनुपात 1:2 है । यह लेंस 6 सेमी दुरी पर स्थित वस्तु के आने वाले प्रकाश की किरणों को समान्तर कर देता है । इसके पृष्ठों की वक्रता त्रिजियाएँ ज्ञात करें । (4.5 सेमी , 9 सेमी )

(8) 15 सेमी फोकस दुरी वाले काँच के उत्तल लेंस को पानी में डुबोने पर इसकी प्रभावी फोकस दुरी क्या होगी । ( 60 सेमी )

(9) 20 सेमी फोकस दुरी वाले काँच के एक उत्तल लेंस को 1.6 अपवर्तनांक वाली बेंजीन में डुबोने पर उसका फोकस दुरी ज्ञात कीजिये । ( 160 सेमी )

(10) 25 सेमी फोकस दुरी वाले काँच के एक उत्तल लेंस को पानी डुबोया गया है । लेंस की फोकस दुरी में हुए परिवर्तन की गणना कीजिये । ( 72.8 सेमी )

(11) एक द्वी – उत्तल लेंस की वक्रता त्रिज्याएँ क्रमशः 10 सेमी एवं 20 सेमी है । इसे 1.76 अपवर्तनांक वाले द्रव में डुबोने पर फोकस दुरी ज्ञात कीजिये । लेंस के पदार्थ का अपवर्तनांक 1.6 है । द्रव में लेंस की प्रकृति भी बतलाइये । (-73.3 सेमी , अपसारी लेंस )

(12) काँच के एक लेंस की वायु में फोकस दुरी 30 सेमी तथा एक द्रव में डुबोने पर फोकस दुरी 120 सेमी है । द्रव का अपवर्तनांक ज्ञात करें । ( 4/3)

◊ लेंस सूत्र

यह सूत्र लेंस की फोकस दुरी , वस्तु दुरी तथा प्रतिबिम्ब दुरी के बीच सम्बन्ध को दर्शाती है

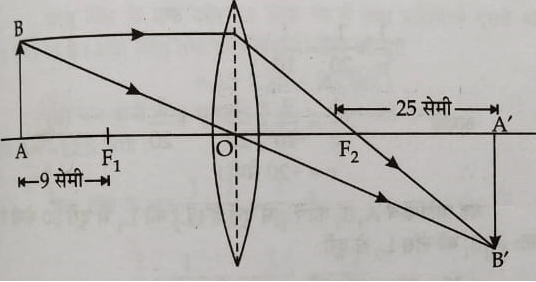
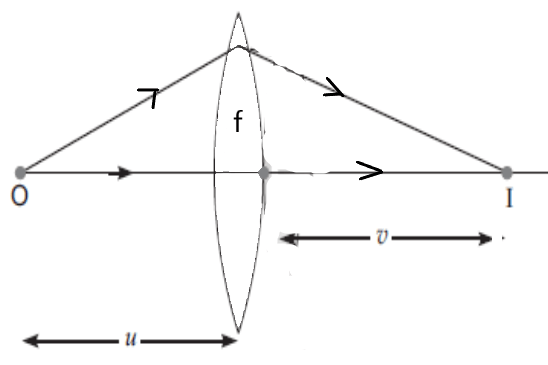
माना की xy एक उत्तल लेंस है जिसका फोकस दुरी फ है । AB एक वस्तु है जिसे लेंस के मुख्य फोकस पर लंबवत रखा गया है , अपवर्तन के बाद जिसका वास्तविक एवं उल्टा प्रतिबिम्ब A’B’ मुख्य फोकस पर बनता है ।

चित्र के अनुसार $\Delta BPA\; \; and \; \; \Delta B'PA'\; \; \; are\; \; \; similar$

$\fn_cm i.e \; \; \frac{B'A'}{BA}=\frac{PA'}{PA}-----(1)$

$also \; \; \Delta MFP\; \; \; and\; \; \; \Delta B'FA'\; \; \; are \; \; similar$

$\fn_cm i.e\; \; \frac{B'A'}{MP}=\frac{FA'}{PF}$

$\fn_cm \because MP=BA$

$\fn_cm \therefore \frac{B'A'}{BA}=\frac{FA'}{PF}-----(2)$

$\therefore \; \; from (1)\; \; and \; \; (2)$

$\fn_cm \Rightarrow \frac{PA'}{PA}=\frac{FA'}{PF}$

$\fn_cm \Rightarrow \frac{PA'}{PA}=\frac{PA'-PF}{PF}$

चिन्ह परिपाटी के अनुसार,

$\fn_cm PA=-u,\; \; PA'=v\; \; and \; \; PF=f$

$\fn_cm \large \therefore \frac{v}{-u}=\frac{v-f}{f}$

$\fn_cm \large \Rightarrow vf=-uv+uf$

दोनों तरफ uvf से भाग देने पर

$\fn_cm \large \Rightarrow \frac{vf}{uvf}=\frac{-uv}{uvf}+\frac{uf}{uvf}$

$\fn_cm \large \Rightarrow \frac{1}{u}=-\frac{1}{f}+\frac{1}{v}$

$\fn_cm \large \left [ \frac{1}{v}-\frac{1}{u}=\frac{1}{f} \right ]$ यह लेंस सूत्र है

रेखीय आवर्धन

रेखीय आवर्धन हमें यह बतलाती है की प्रतिबिम्ब वस्तु से कितना गुना बड़ा या छोटा है । अर्थात किसी लेंस द्वारा बनने वाले प्रतिबिम्ब के आकार तथा वस्तु के आकार के अनुपात को लेंस का रेखीय आवर्धन कहते है । इसे m द्वारा सूचित किया जाता है ।

$\fn_cm \large i.e\; \;\; \left [ m=\frac{h_{2}}{h_{1}} \right ]$

जहाँ $\large h_{2}$ – प्रतिबिम्ब की ऊंचाई

$\large h_{1}$ – वस्तु की ऊंचाई

$\fn_cm from\; above\;figure \;\; \frac{B'A'}{BA}=\frac{PA'}{PA}$

$\fn_cm \large \Rightarrow \frac{-h_{2}}{h_{1}}=\frac{v}{-u}$

$\fn_cm \large \left [ m=\frac{v}{u} \right ]$

लेंस द्वारा बने प्रतिबिम्बों की प्रकृति

1. उत्तल लेंस द्वारा

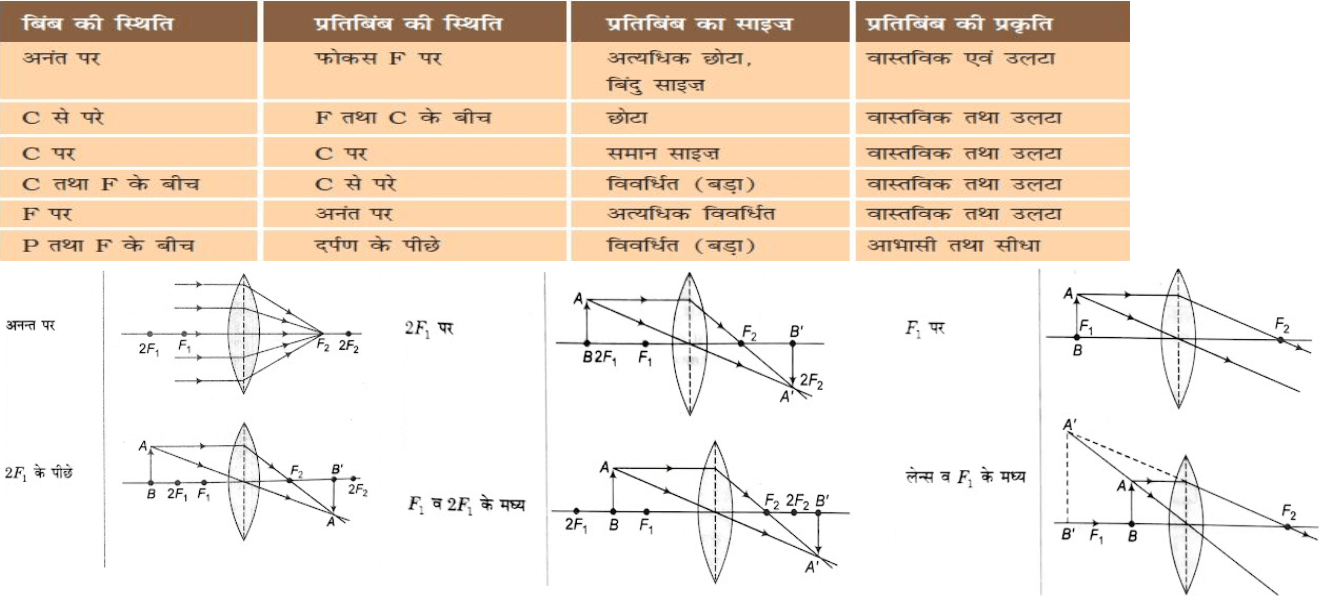
2 . अवतल लेंस द्वारा

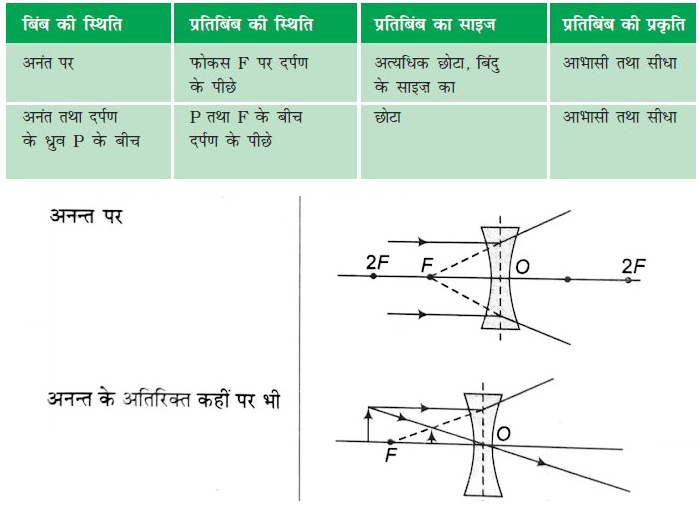
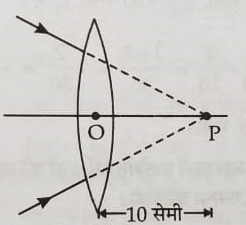
अभ्यासार्थ प्रश्न 3

(1) एक वस्तु एक उत्तल लेंस के सामने इतनी दूर पर रखी जाती है की उसका वास्तविक प्रतिबिम्ब उतने ही आकार का बनता है। जब वस्तु को लेंस की ओर 16 सेमी खिसका देते है तब वास्तविक प्रतिबिम्ब वस्तु से तीन गुना बड़ा बनता है । लेंस की फोकस दुरी ज्ञात कीजिये ।( 24 सेमी )

(2) 21 सेमी फोकस दुरी के एक अवतल लेंस के सामने 14 सेमी की दुरी पर 3 सेमी आकार की एक वस्तु स्थित है । लेंस द्वारा बने प्रतिबिम्ब का वर्णन कीजिये । यदि वस्तु को लेंस से दूर हटाया जाये , तो क्या होगा । (v=-8.4 सेमी , h2=1.8 सेमी आभासी तथा सीधा )

(3) 3 सेमी ऊँची एक वस्तु 21 सेमी फोकस दुरी के एक अवतल लेंस के सामने 14 सेमी की दुरी पर रखी है । लेंस द्वारा निर्मित प्रतिबिम्ब का वर्णन करें । क्या होता है जब वस्तु लेंस से दूर हटती जाती है । (8.4 सेमी , सीधा , आभासी ऊंचाई = 1.8 सेमी )

(4) एक किरण पुंज किसी बिंदु P पर अभिसरित होता है । किरणों के मार्ग में P से 12 सेमी पहले ही एक लेंस को रखने पर यह किरण पुंज कहाँ अभिसरित होगा , यदि (a) लेंस 20 सेमी दुरी का एक उत्तल लेंस हो (b) लेंस 16 सेमी फोकस दुरी का एक अवतल लेंस हो ( लेंस से 7.5 सेमी दूर बिंदु P की ओर , लेंस से 18 सेमी दूर बिंदु P की ओर )

(5) सूर्य की समान्तर किरणे 15 सेमी फोकस दुरी के अवतल लेंस पर गिरती है । इस लेंस से 25 सेमी की दुरी पर 20 सेमी फोकस दुरी का एक उत्तल लेंस स्थित है । सूर्य का प्रतिबिम्ब प्राप्त करने के लिए पर्दा कहाँ रखना होगा । ( उत्तल लेंस से 40 सेमी आगे )

(6) 20 सेमी फोकस दुरी के एक अभिसारी लेंस के सामने एक वस्तु कहाँ रखी जाये जिससे की दुगने आकार का वास्तविक प्रतिबिम्ब बन जाये । ( 30 सेमी )

(7) संलग्न चित्र से लेंस की फोकस दुरी ज्ञात कीजिये । ( 15 सेमी )

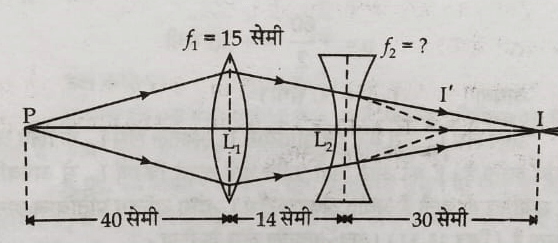
(8) दिए गए चित्र में पहले लेंस की फोकस दुरी दिया हुआ है । दूसरे लेंस की फोकस दुरी ज्ञात करें । ( -15 सेमी )

(9) माना की उत्तल लेंस पर प्रकाश की किरणे निम्न चित्र के अनुसार पड़ रही है । यदि लेंस की फोकस दुरी 30 सेमी है तो प्रतिबिम्ब की स्थिति ज्ञात करें । ( 5.5 सेमी )

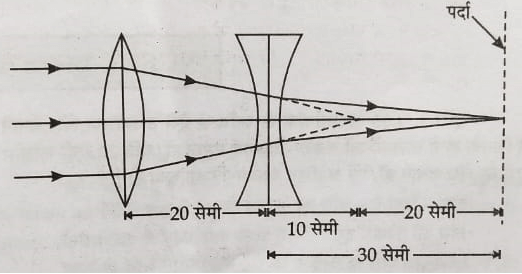
(10) दिए गए चित्र में प्रकाश की किरणे अनंत से आ रही है । अवतल लेंस की फोकस दुरी ज्ञात करें । (-15 सेमी )

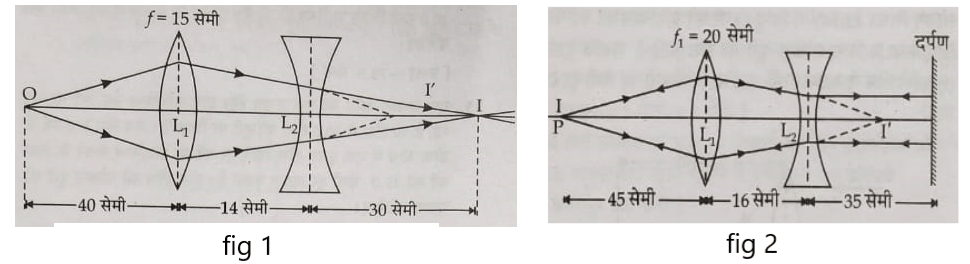
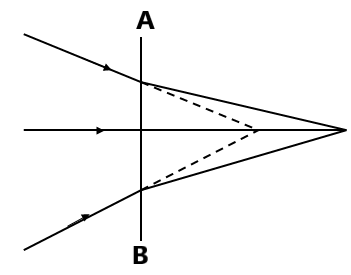
(11) चित्र 1 और 2 में दूसरे लेंस की फोकस दुरी ज्ञात करें । (-15 सेमी , -20 सेमी )

लेंस की क्षमता

हम जानते हैं कि किसी लेंस की प्रकाश किरणों को अभिसरित अथवा अपसरित करने की क्षमता उसकी फोकस दूरी पर निर्भर करती है। किसी लेंस द्वारा प्रकाश किरणों को अभिसरण या अपसरण करने की मात्रा (degree) को उसकी क्षमता के रूप में व्यक्त किया जाता है। अर्थात जिस लेंस की क्षमता अधिक ( फोकस दुरी कम ) होगी वह लेंस प्रकाश की किरणों को अधिक अभिसरित या अपसरित करती है ।

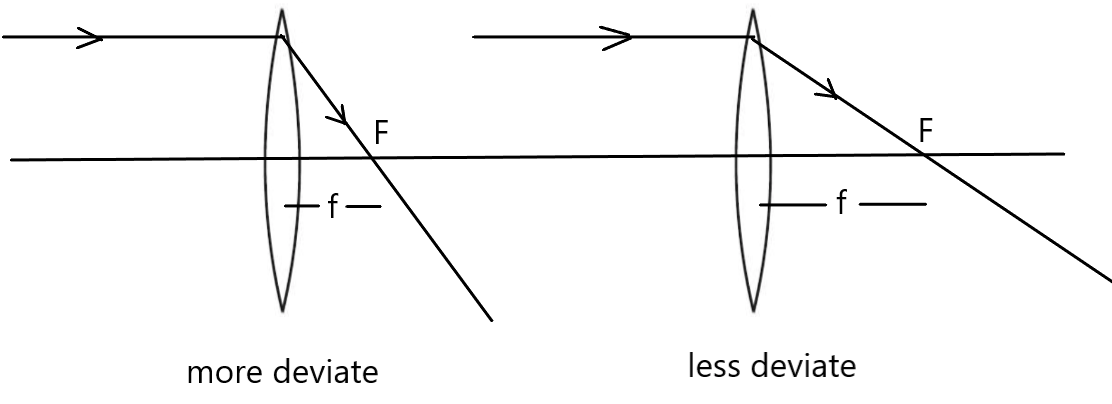
किसी लेंस की क्षमता को लेंस की फोकस दुरी के व्युत्क्रम के रूप में परिभाषित किया जाता है ।इसे P द्वारा सूचित किया जाता है ।

$\fn_cm \large i.e \; \; \left [ P=\frac{1}{f} \right ]$

इसका S.I मात्रक /m या dioptre (D) होता है । उत्तल लेंस का क्षमता +ve तथा अवतल लेंस की क्षमता -ve होती है

संपर्क में लेंस

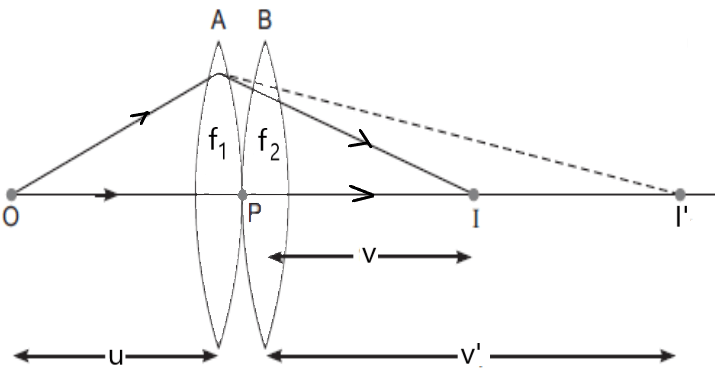
माना की दो पतले उत्तल लेंस A तथा B को एक ही अक्ष पर परस्पर संपर्क में रखा गया है जिसका फोकस दुरी क्रमशः $\fn_cm f_1$ तथा $\fn_cm f_2$ है । माना की एक बिंदुअत वस्तु O जिसे जिसे मुख्य अक्ष में u दुरी पर रखा गया है ।

पहले लेंस A के लिए, O वस्तु है जिसका एक वास्तविक प्रतिबिम्ब I’ लेंस के दूसरी और v’ दुरी पर बनता है ।

अर्थात हम लिख सकते है

$\fn_cm \large \frac{1}{v'}-\frac{1}{u}=\frac{1}{f_{1}}-----(1)$

यह प्रतिबिम्ब I’ लेंस B के लिए एक आभासी वस्तु का काम करती है ।

अर्थात , लेंस B के लिए , I’ एक आभासी वस्तु है , जिसका एक वास्तविक प्रतिबिम्ब I लेंस से v दुरी पर बनता है ।

अर्थात हम लिख सकते है

$\fn_cm \large \frac{1}{v}-\frac{1}{v'}=\frac{1}{f_{2}}-----(2)$

समीकरण (1) और (2) को जोड़ने पर

$\fn_cm \large \frac{1}{v}-\frac{1}{u}=\frac{1}{f_{1}}+\frac{1}{f_{2}}-----(a)$

यदि इन दोनों लेंसों के स्थान पर एक ऐसा पतला लेंस रखा जाए जो O पर स्थित वस्तु का प्रतिबिम्ब I पर ही बनाए, तो यह लेंस दोनों लेंसों का समतुल्य लेंस होगा।

यदि समतुल्य लेंस की फोकस दुरी $\fn_cm f$ हो तो हम लिख सकते है

$\fn_cm \large \frac{1}{v}-\frac{1}{u}=\frac{1}{f}-----(b)$

समीकरण (a) तथा (b) से

$\fn_cm \large \left [ \frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}} \right ]$

यदि पहले लेंस की क्षमता $\fn_cm p_1$ तथा दूसरे लेंस की क्षमता $\fn_cm p_2$ हो , तो लेंस की समतुल्य क्षमता होगी

$\fn_cm \large \left [ p=p_{1}+p_{2} \right ]$

अभ्यासार्थ प्रश्न 1

(1) 3.5D तथा -4.75D क्षमता वाले दो लेंस परस्पर संपर्क में रखे गए है । संयुक्त लेंस की फोकस दुरी ज्ञात करे । ( -80 सेमी )

(2) 30 सेमी फोकस दुरी का एक उत्तल लेंस 20 सेमी फोकस दुरी के एक अवतल लेंस के संपर्क में रखा गया है । इस युग्म की फोकस दुरी तथा क्षमता ज्ञात कीजिये । ( 60 सेमी , -1.67D)

(3) 25 सेमी फोकस दुरी के एक उत्तल लेंस के संपर्क में एक अवतल लेंस रखा गया है । यदि यह युग्म 50 सेमी फोकस दुरी वाले अभिसारी लेंस की भांति व्यवहार करे तो अवतल लेंस की क्षमता तथा फोकस दुरी ज्ञात कीजिये । ( -2D, – 50 सेमी )

(4) 15 सेमी और 30 सेमी फोकस दुरी के दो पतले उत्तल लेंसों को एक दूसरे के संपर्क में रखा जाता है । संयोजित लेंस की शक्ति क्या होगी । (10D)

(5) +5D तथा -7D क्षमता के दो पतले लेंसों को संपर्क में रखकर बनाये गए संयुक्त लेंस की क्षमता एवं फोकस दुरो ज्ञात करें । संयुक्त लेंस अपसारी या अभ्सारी होगा ।( -2D, -50 सेमी , अपसारी )

(6) दो पतले लेंसों को जिनकी क्षमताएँ +15.5D तथा -5.5D है , सटाकर रखा गया है । इस सयोंग से 30 सेमी की दुरी पर 3 सेमी लम्बी वस्तु राखी गई है । प्रतिबिम्ब की स्थिति तथा लम्बाई ज्ञात करें । (15 सेमी , 1.5 सेमी )

(7) दो पतले लेंस जिनकी क्षमताएँ क्रमशः +3D तथा -5D है, मिलकर एक संयुक्त लेंस बनाया गया है । इस संयुक्त लेंस से 50 सेमी की दुरी पर रखी वस्तु के प्रतिबिम्ब की स्थिति ज्ञात कीजिये ।

(8) एक उत्तल और अवतल लेंस सटा हुआ है और उनका योग अभिसारी निकाय बन जाता है , जिसकी फोकस दुरी 20 सेमी है । यदि उत्तल लेंस की फोकस दुरी 10 सेमी हो , तब अवतल लेंस की फोकस दुरी क्या होगी ? ( -20 सेमी )

(9) दो पतले उत्तल लेंस जिनकी क्षमताएँ 5D तथा 2D है , एक दूसरे से 20 सेमी की दुरी पर समाक्षीय रूप से स्थित है । समतुल्य लेंस की फोकस दुरी एवं क्षमता ज्ञात कीजिये ।

(10) दो पतले लेंस जिनमे से प्रत्येक की फोकस दुरी 25 सेमी है , एक दूसरे के संपर्क में रखे हुए है । इनमे 15 सेमी की दुरी पर एक वस्तु रखने पर वस्तु और प्रतिबिम्ब के बीच कितनी दुरी होगी , जबकि दोनों लेंस (a) उत्तल (b) अवतल है ?

NOTE

$\fn_cm {\color{Red} \textbf{1.}}$ यदि संपर्क में रखे लेंसों का आवर्धन क्रमशः $\fn_cm m_1, m_2, m_3, ......$ हो तो लेंसों का का समतुल्य आवर्धन होगा

$\fn_cm \left [ m=m_1\times m_2\times m_3 \times....... \right ]$

$\fn_cm {\color{Red} \textbf{2.}}$ हम जानते है की $\fn_cm \large \frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}}$

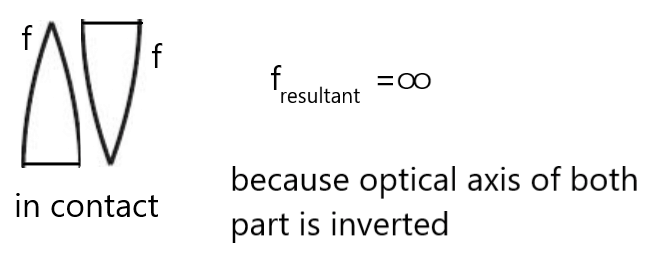
इनमे से यदि एक लेंस उत्तल तथा दूसरा लेंस अवतल हो तो , हम लिख सकते है

$\fn_cm \large \frac{1}{f}=\frac{1}{f_{1}}-\frac{1}{f_{2}}$

$\fn_cm \large \frac{1}{f}=\frac{f_{2}-f_{1}}{f_{1}f_{2}}$

$\fn_cm \large \therefore \left [ f=\frac{f_{1}f_{2}}{f_{2}-f_{1}} \right ]$

case I – यदि $\fn_cm \large f_{1}=f_{2}$ , तब $\fn_cm \large f\rightarrow \infty$ , अर्थात समतुल्य लेंस एक काँच की पट्टी की तरह व्यवहार करती है ।

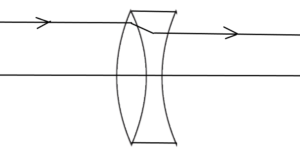
case II- यदि $\fn_cm \large f_{1}>f_{2}$ , तब $\fn_cm \large f$ -ve होगा , तथा यह एक अवतल लेंस की तरह व्यवहार करेगी ।

case III- यदि $\fn_cm \large f_{1}<f_{2}$ , तब $\fn_cm \large f$ +ve होगा, तथा यह एक उत्तल लेंस की तरह व्यवहार करेगी ।

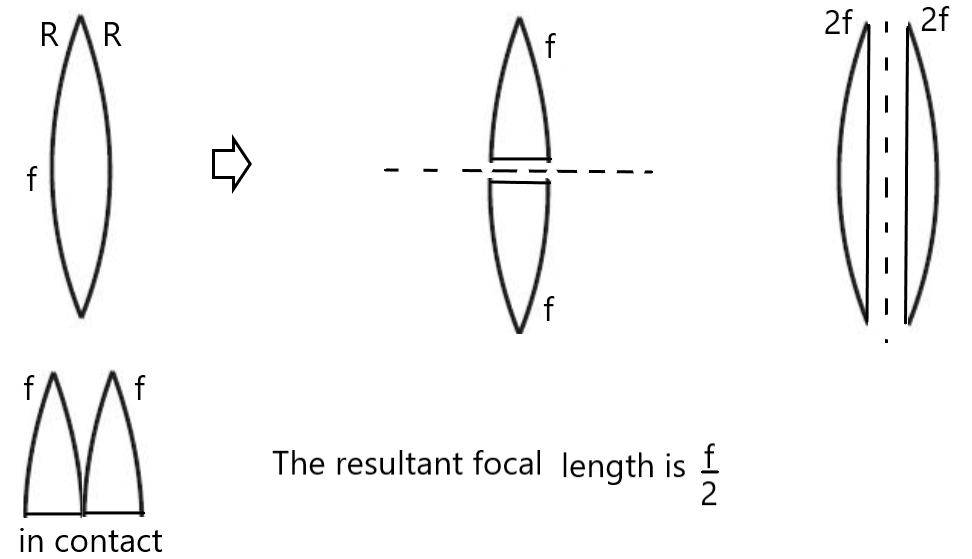
$\fn_cm {\color{Red} \textbf{3.}}$ यदि दो लेंस जिसकी फोकस दुरी $\fn_cm f_1$ तथा $\fn_cm f_2$ है , दोनों $\fn_cm d$ दुरी पर स्थित हो तो उन दोनों का समतुल्य फोकस दुरी होगा ।

$\fn_cm \large \left [ \frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}}-\frac{d}{f_{1}f_{2}} \right ]$

$\fn_cm {\color{Red} \textbf{4.}}$ यदि कोई लेंस तीन प्रकार के अलग अलग माध्यम से मिल कर बनी है , तो उस लेंस के तीन फोकस दुरी होंगे तथा किसी वस्तु के लिए तीन प्रतिबिम्ब प्राप्त होंगे ।

$\fn_cm {\color{Red} \textbf{5.}}$

$\fn_cm {\color{Red} \textbf{6.}}$

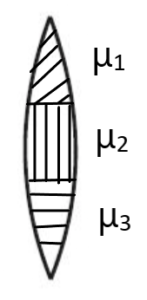
$\fn_cm {\color{Red} \textbf{7.}}$ किसी तरल के अंदर एक लेंस की क्षमता होगी $\fn_cm \large \left [ p=\frac{\mu _{liquid}}{f} \right ]$

$\fn_cm {\color{Red} \textbf{8.}}$ किसी दर्पण का फोकस दुरी सिर्फ दर्पण के वक्रता त्रिज्या पर निर्भर करती है $\fn_cm \large f=\frac{R}{2}$ , परन्तु किसी लेंस के फोकस दुरी $\fn_cm \large \mu_{1}, \mu_{2}, R{1}\;and \; R_{2}$ पर निर्भर करती है ।

$\fn_cm {\color{Red} \textbf{9.}}$

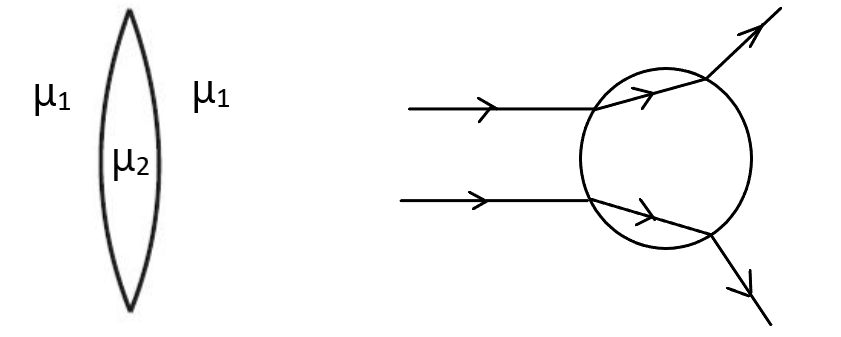
हम जानते है की

$\fn_cm \large \frac{1}{f}=(\frac{\mu_{2} }{\mu_{1} }-1)\left ( \frac{1}{R_{1}}-\frac{1}{R_{2}} \right )$

यदि $\fn_cm \large \mu_{1}> \mu_{2}$ , तब फोकस दुरी f -ve होगी । अर्थात यह उत्तल लेंस न होकर अवतल लेंस की तरह व्यवहार करती है जबकि यह दिखने में उत्तल लेंस की तरह ही होती है । उसी प्रकार अवतल लेंस भी उत्तल लेंस की तरह व्यवहार करती है । ex- पानी के अंदर हवा का बुलबुला

$\fn_cm {\color{Red} \textbf{10.}}$ यदि प्रकाश की किरणे सतह के लम्बवत आपतित होती है (i=0) तथा यदि $\fn_cm \large \mu_{1}=\mu_{2}$ तो इन condition में प्रकाश का अपवर्तन नहीं होगा।

प्रश्न

1. किसी लेंस की फोकस दुरी किन किन बातों पर निर्भर करती है ।

2 .एक लेंस जिसकी दोनों वक्रता त्रिज्याएँ अलग अलग है , अपने अक्ष पर स्थित वस्तु का प्रतिबिम्ब बना रहा है । यदि लेंस को उलट कर रख दिया जाये तो क्या प्रतिबिम्ब की स्थिति बदल जाएगी ।

3 . यदि किसी लेंस का कुछ भाग को ढक दिया जाये तो उससे बनने वाले प्रतिबिम्ब पर क्या प्रभाव पड़ेगा ?

4 . सौर ऊर्जा एकत्र करने के लिए कौन सा लेंस अधिक उपयुक्त है , उत्तल या अवतल ।

5 . किस दशा में लेंस की प्रथम एवं द्वितीय फोकस दुरी का मान बराबर नहीं होता है ।

6 . एक उत्तल लेंस द्वारा सूर्य का प्रतिबिम्ब लेंस से 20 सेमी की दुरी पर बनता है । प्रतिबिम्ब कहाँ बनेगा यदि (a) उसी क्षमता का दोगुने द्वारक वाला लेंस लिया जाये (b) उतने ही द्वारक का दुगुने क्षमता का लेंस लिया जाये ।

7 . दिए गए चित्र में बतलाइये लेंस AB अवतल है या उत्तल ।

8 . एक उत्तल लेंस के दोनों पृष्ठों की वक्रता त्रिज्याएँ परस्पर बराबर है । यदि लेंस के पदार्थ का अपवर्तनांक 1.5 हो , तो सिद्ध कीजिये की लेंस की फोकस दुरी उसकी वक्रता त्रिज्या के बराबर होगी ।

9 . जल के अंदर वायु का बुलबुला किस लेंस की भांति व्यवहार करेगा , चित्र द्वारा समझाइये ।

10 . एक लेंस एक ऐसे माध्यम में रखा है जिसमे यह एक साधारण प्लेट की भांति व्यवहार करता है । लेंस तथा माध्यम के अपवर्तनांक में क्या सम्बन्ध है ।

11 . किसी लेंस की क्षमता वायु की तुलना में जल से अधिक होगी अथवा कम ।

12 . एक अवतल लेंस द्वारा अनंत पर स्थित वस्तु का प्रतिबिम्ब लेंस के फोकस पर बनता है । यदि वस्तु फोकस पर राखी जाये , तो उसका प्रतिबिम्ब कहाँ बनेगा ।

13 . 10D क्षमता वाले उत्तल लेंस से 20 सेमी की दुरी पर 2 सेमी लम्बी वस्तु स्थित है । प्रतिबिम्ब की लम्बाई एवं प्रकृति बताइये ।

14 . लेंस की क्षमता से क्या तात्पर्य है , डाइऑप्टर की परिभाषा लिखिए ।

15 . +10D तथा -10D क्षमता वाले दो लेंस परस्पर संपर्क में रखे है । इस संयोग की क्षमता तथा फोकस दुरी बतलाइये । चित्र सहित समझाइये ।

16 . एक अवतल लेंस एक ऐसे माध्यम में डुबोया जाता है जिसका अपवर्तनांक लेंस के माध्यम के अपवर्तनांक से अधिक है । बतलाइये की लेंस किस प्रकार व्यवहार करेगा ।

17 . दिए गए चित्र में यदि दोनों पृष्ठों की वक्रता त्रिज्याएँ समान है । क्या इसे लेंस कहा जा सकता है ? इसकी क्षमता कितनी होगी तथा इसका उपयोग कहाँ हो सकता है । यदि दोनों त्रिज्याएँ अलग अलग हो तो यह किस प्रकार के लेंस की भांति व्यवहार करेगा ।

18 . एक लेंस जिसकी फोकस दुरी f है , एक दीप्त वस्तु का परदे पर m गुना बड़ा प्रतिबिम्ब बनाता है । तो दिखलाइये की परदे की लेंस से दुरी (m+1) है

19 . एक वस्तु तथा पर्दे के बीच की दुरी a है तथा इसके बीच f फोकस दुरी का उत्तल लेंस रखा है तो सिद्ध कीजिये की वस्तु का पर्दे पर प्रतिबिम्ब प्राप्त करने के लिए a का न्यूनतम मान 4f होना चाहिए ।

20 . लेंस के आवर्धन से क्या अभिप्राय है ? इसका सूत्र लिखिए ।

21 . किसी लेंस के लिए निम्नलिखित सूत्र प्राप्त कीजिये । $\fn_cm \large \left [ \frac{1}{f}=\left ( \frac{\mu _{2}}{\mu _{1}}-1 \right )\left ( \frac{1}{R_{1}}-\frac{1}{R_{2}} \right ) \right ]$

22 . लेंस की क्षमता से आप क्या समझते है ? संपर्क में स्थित दो पतले लेंसों के संयोग की क्षमता के लिए व्यंजक प्राप्त करें ।

23 . सिद्ध कीजिये की संपर्क में रखे दो पतले लेंसों के संयोग की फोकस दुरी f का मान समीकरण से प्राप्त होता है । $\fn_cm \large \frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}}$

24 . लेंस सूत्र से क्या अभिप्राय है ? अवतल लेंस के लिए “लेंस सूत्र” का व्यंजक प्राप्त करें ।