एकसमान वृत्तीय गति :-
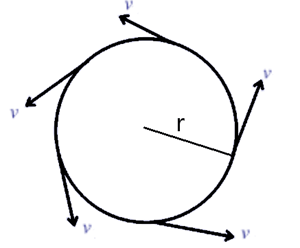
जब कोई कण एक निश्चित बिंदु को केंद्र मानकर उसके चरों ओर एक वृत्तीय मार्ग पर अचर चाल से गति करता है , तो उसकी गति को समरूप वृत्तीय गति कहते है।
इस गति में वस्तु का चाल स्थिर है , परन्तु दिशा में परिवर्तन के कारण इसकी वेग में परिवर्तन होता है अतः यह एक ऐसे एकसमान त्वरित गति का उदहारण है जिसमे इसकी चाल नियत रहती है।
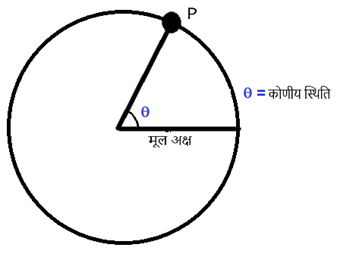
कोणीय स्थिति :- वृत्तीय गति करते हुए किसी कण के स्थिति सदिश द्वारा उसके मूल अक्ष पर बनाए गए कोण को उसका कोणीय स्थिति कहते है। इसे द्वारा सूचित किया जाता है। इसका S.I मात्रक रेडियन (rad) होता है।
कोणीय विस्थापन :- वृत्तीय गति करता हुआ किसी कण द्वारा किसी समय अंतराल में उसके कोणीय स्थिति के परिवर्तन को उस वस्तु का कोणीय विस्थापन कहते है।
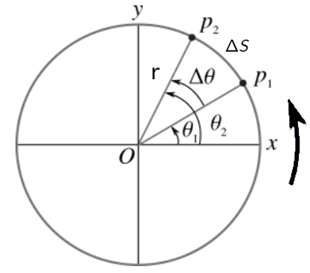
चित्र में कण का कोणीय विस्थापन है।
इसका S.I मात्रक रेडियन (rad) होता है।
हम जानते है की किसी वृत्तखंड में
![]()
कोणीय वेग :- वृत्तीय गति करता हुआ कोई कण द्वारा कोणीय विस्थापन की दर को उसका कोणीय वेग कहते है।
अर्थात औसत कोणीय वेग
जहाँ समय अंतराल में तय किया गया कोणीय विस्थापन है। इसका S.I मात्रक रेडियन/ सेकंड (rad/sec) होता है।
किसी कण का क्षणिक कोणीय वेग / कोणीय वेग
कोणीय वेग तथा रेखीय वेग में सम्बन्ध :-
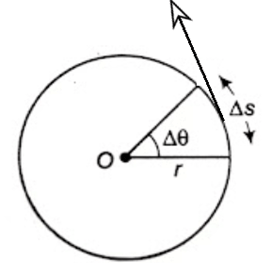
माना की कोई कण समय में r त्रिज्या की वृत की परिधि पर दुरी तय करता है।
तो कोणीय विस्थापन
दोनों तरफ से भाग देने पर
दोनों तरफ limit लगाने पर
वृत्तीय गति में रेखीय वेग की दिशा हमेशा वृत की स्पर्श रेखा के अनुदिश होती है।

NOTE:- यदि कोई ढृढ़ पिंड किसी अक्ष के चरों ओर घूर्णन गति करती है तो सभी कणो का कोणीय वेग समान रहता है , परन्तु उनके रेखीय वेग भिन्न भिन्न होते है। जो कण अक्ष से जितनी अधिक दुरी पर होता है , उसका रेखीय वेग उतना ही अधिक होता है ( )
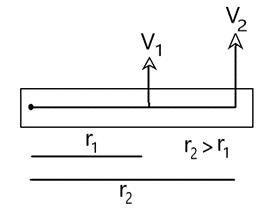
r=0 के लिए v=0
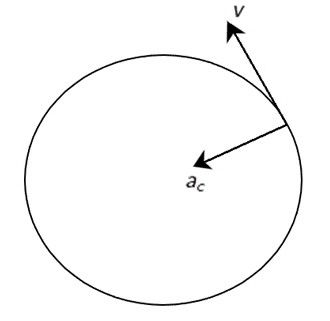
अभिकेंद्र त्वरण :-
जब कोई कण एकसमान वृत्तीय गति में गति करता है तो कण की चाल तो अचर रहती है परन्तु उसकी दिशा निरंतर बदलती रहती है। जिसका कारण कण में एक त्वरण होता है तथा जिसकी दिशा हमेशा वृत के केंद्र की ओर होती है। इसे अभिकेंद्र त्वरण कहते है।
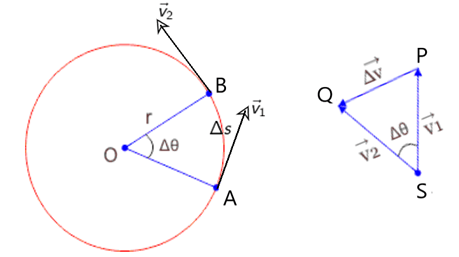
माना की कोई कण r त्रिज्या के वृत्तीय पथ पर नियत चाल v से गति कर रहा है। माना की समय अंतराल में कण A से B तक पहुँचती है तथा इस समय अंतराल में कण का कोणीय विस्थापन है तथा दुरी है। A पर कण का वेग है तथा B पर कण का वेग है।
वेग का अंतर प्राप्त करने के लिए एक दूसरे चित्र का निर्माण करते है , जैसा की चित्र में दिखाया गया है। यहाँ पर वेग के अंतर को प्रदर्शित करता है।
पहले चित्र में
दूसरे चित्र में , छोटे कोण के लिए PQ को हम चाप के रूप में मान सकते है। अर्थात
समीकरण (1) और (2) से
दोनों तरफ से भाग देने पर
दोनों तरफ limit करने पर
यह त्वरण अभिकेंद्र त्वरण कहलाती है तथा जिसकी दिशा की ओर अर्थात केंद्र की ओर होती है।