♦ विधुत धारा ♦
विधुत आवेशों के प्रवाह से ही विधुत धारा उत्पन्न होती है । किसी पदार्थ के अनुप्रस्थ काट में से आवेश की प्रवाह की दर को विधुत धारा कहते है ।
अर्थात 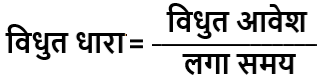
( औसत धारा )
किसी समय क्षणिक धारा होगी
विधुत धारा के पास परिमाण तथा दिशा दोनों होते हैं परंतु यह सदिश राशि नहीं है क्योंकि यह सदिशों का योग का त्रिभुज नियम का पालन नहीं करता है ।
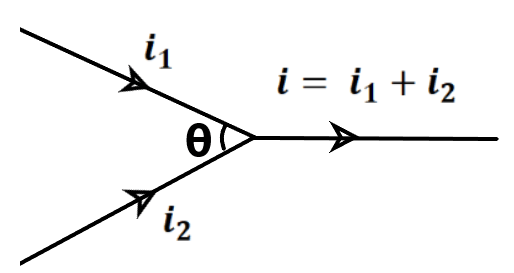
विधुत धारा की दिशा +ve आवेश की दिशा की ओर तथा -ve आवेश की दिशा के विपरीत होती है।विधुत धारा का S.I मात्रक C/s या एम्पियर(A) होता है ।
चूँकि यदि t= 1 sec तो
अर्थात ” किसी परिपथ में एक सेकंड में जितना आवेश प्रवाहित होता है उसे ही उसे परिपथ की विधुत धारा कहते हैं ।”
यदि t= 1 sec तथा Q= 1 Coulomb तो i= 1 Ampere
अर्थात ” 1 एम्पियर विधुत धारा का वह मान होता है जब किसी परिपथ में एक सेकंड में एक कूलम्ब आवेश प्रवाहित हो ”
NOTE:-
यदि कोई आवेश q , एक वृतीय पथ जिसकी त्रिज्या r है , v वेग से घूम रही है । तो उसके परिधि के परितः किसी बिंदु पर समतुल्य विधुत धारा का मान होगा ।
जहाँ
आवेश की आवृत्ति है ।
विधुत धारा दो प्रकार की होती है
(1) दिष्ट धारा :- जिसकी दिशा समय के साथ नहीं बदलती है
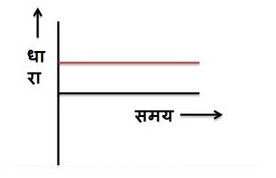
(2) प्रत्यावर्ती धारा :- जिसका परिमाण तथा दिशा दोनों आवर्ती रूप से बदलती रहती है।
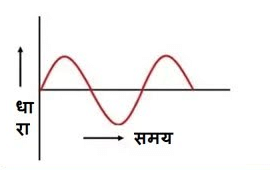
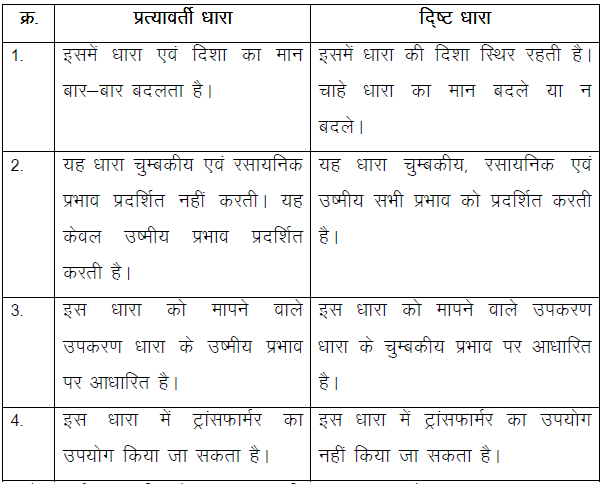
पदार्थों में धारा वाहक
ठोसों में धारा वाहक
(1) चालक में :- मुक्त इलेक्ट्रॉन्स
(2) कुचालक में :- चूँकि कुचालक में मुक्त इलेक्ट्रॉन नहीं होते हैं इस प्रकार इसमें धारा वाहक नहीं होते हैं।
(3) अर्धचालक में :- मुक्त इलेक्ट्रॉन्स तथा +ve विवर ( होल्स )
द्रव में धारा वाहक
कुछ द्रव जो विधुत धारा को प्रवाहित होने देते हैं तथा साथ ही आयन में विघटित हो जाते हैं विद्युत अपघटय (Electrolyte) कहलाते हैं।
जैसे – CuSo4 विलयन , NaCl विलयन , H2SO4 विलयन , AgNO3 इत्यादि ।
वाह्य विधुत क्षेत्र के प्रभाव में विद्युत अपघटय के पॉजिटिव तथा नेगेटिव आयन निश्चित दिशा में गतिमान होते हैं इस प्रकार विधुत धारा प्रवाहित होती है।
अतः द्रवों में +ve तथा -ve आयन्स धारा वाहक होते हैं।
गैसों में धारा वाहक
सामान्यतः गैसें विधुत की कुचालक होती है परंतु जब इस पर अल्प दाब पर उच्च विभव आरोपित किया जाता है तो यह आयनित होकर चालक की तरह व्यवहार करती है । अर्थात आयनित गैसों में +ve आयन्स तथा -ve इलेक्ट्रॉन्स होते है । अतः गैसों में आयन्स तथा मुक्त इलेक्ट्रॉन्स धारा वाहक होते है ।
धारा घनत्व
किसी चालक में किसी बिंदु पर तल के लंबवत प्रति एकांक क्षेत्रफल से गुजरने वाली विधुत धारा को धारा घनत्व कहते हैं । इसे J द्वारा सूचित किया जाता है। यदि विधुत धारा समान रूप से वितरित हो तो,
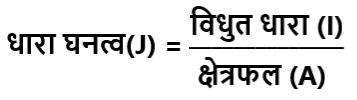
धारा घनत्व चालक के अंदर किसी बिंदु का (ना की संपूर्ण चालक का) एक गुण है। यह एक सदिश राशि है जिसकी दिशा विधुत धारा की दिशा की ओर होती है।
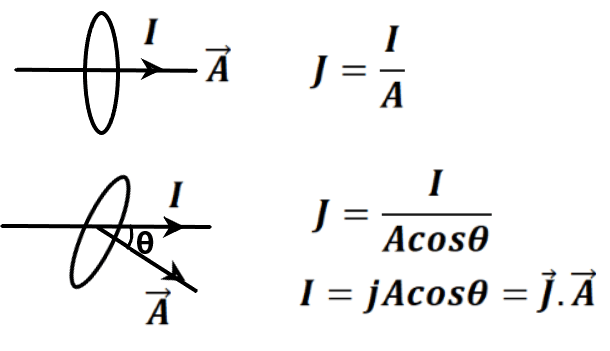
धारा घनत्व का S.I मात्रक A/m² तथा विमीय सूत्र होता है।
| (1) यदि किसी तार से 10 sec में 50μC आवेश प्रवाहित होता है तो तार में प्रवाहित विधुतधारा का मान ज्ञात करें ?
(2) एक तार में 20 μA की धारा 30 sec तक प्रवाहित होती है ज्ञात कीजिए (a) तार से स्थानांतरित आवेश (3) किसी चालक में बिंदु P से Q की ओर (3) हाइड्रोजन परमाणु में इलेक्ट्रॉन (4) किसी तार का व्यास 0.2 cm है। इससे 10A की धारा प्रवाहित हो रही है । तार में धारा घनत्व की गणना करें । (5) किसी विधुत परिपथ में जब धारा घनत्व बढ़कर 600 A/cm² हो जाता है तो इसके फ्यूज की तार पिघल जाती है । यदि तार में प्रवाहित धारा को 0.4 A ही सीमित रखना हो तो तार का व्यास कितना होना चाहिए ? (6) यदि किसी तार में 40 min में 0.8 मोल इलेक्ट्रॉन्स प्रवाहित होते हैं (a) तार से गुजरने वाला कुल आवेश कितना होगा ? (7) एक इलेक्ट्रान पुंज का परिच्छेद क्षेत्रफल 1 mm² है । किसी परिच्छेद के लम्बवत प्रति सेकण्ड |
संवहन वेग / अपवाह वेग /अनुगमन वेग (Drift Velocity)
बाह्य विधुत क्षेत्र की अनुपस्थिति में धातु के मुक्त इलेक्ट्रॉन सभी दिशाओं में अनियमित रूप से गति करते रहते हैं जिसके कारण इलेक्ट्रोनो का किसी निश्चित दिशा में प्रवाह नहीं होता अतः विधुत धारा शून्य होती है ।
लेकिन विधुत क्षेत्र की उपस्थिति में सभी इलेक्ट्रोनो में विधुत क्षेत्र की दिशा के विपरीत एक बल लगता है लेकिन आयनो से टक्कर के क्रम में मुक्त इलेक्ट्रॉन्स टेढ़े-मेढ़े पथ में चलते हैं।
इस प्रकार इलेक्ट्रॉन विधुत क्षेत्र की दिशा के विपरीत प्रणोदित बल की दिशा में एक छोटे एक समान वेग जिसे संवहन वेग कहते हैं से चलते हैं।
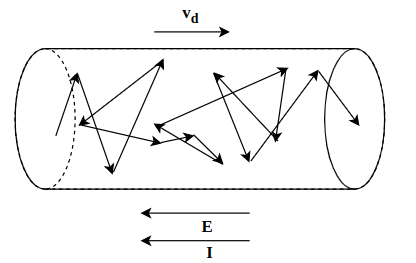
यदि दो क्रमागत टककारों के बीच का माध्य समय हो , जिसे विश्रांति समय कहा जाता है । तो संवहन वेग का मान होगा
NOTE:
इलेक्ट्रॉन का क्षणिक वेग
इलेक्ट्रॉन का अपवाह वेग
विश्रांति समय
चालक में अनुगमन वेग के कारण ही विधुत धारा प्रवाहित होते हैं
, अर्थात विधुत क्षेत्र अधिक होने पर अनुगमन वेग भी अधिक होगा ।
गतिशीलता
किसी आवेश वाहक की गतिशीलता को इसके अपवाह वेग तथा आरोपित विधुत क्षेत्र के अनुपात के रूप में परिभाषित किया जाता है । अर्थात प्रति एकांक विधुत क्षेत्र आवेशों के अपवाह वेग को आवेशों की गतिशीलता कहते है ।
अर्थात
इसका S.I मात्रक तथा विमीय सूत्र
होता है ।
धारा चालक की गतिशीलता उसके द्रव्यमान के व्युत्क्रणुपाती होता है । जैसे अर्धचालक में किसी इलेक्ट्रान की गतिशीलता , विवर ( होल्स ) की तुलना में अधिक होती है , क्योंकि इलेक्ट्रान का द्रव्यमान होल की तुलना में बहुत ही कम होती है ।
♦ अपवाह वेग तथा विधुत धारा में सम्बन्ध ♦
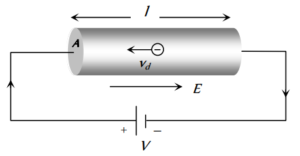
माना की l लम्बाई का एक चालक है जिसका समरूप अनुप्रस्थ क्षेत्रफल A है । माना की चालक के प्रति इकाई आयतन में मुक्त इलेक्ट्रॉन्स की संख्या n है ।
चालक में मुक्त इलेक्ट्रॉन्स की कुल संख्या = n × चालक का आयतन = nAl
∴ चालक में मुक्त इलेक्ट्रॉन्स का कुल आवेश Q= e(nAl)
चालक की लम्बाई में से आवेश को प्रवाहित होने में लगा समय होगा ।
∴ चालक में विधुत धारा होगी
यहाँ पर
उसी प्रकार
यहाँ अर्थात जब किसी चालक के असमान परिच्छेद के क्षेत्रफल से स्थायी धारा प्रवाहित होती है , तो अनुगमन वेग अनुप्रस्थ परिच्छेद के क्षेत्रफल के व्यत्क्रमानुपाती होता है
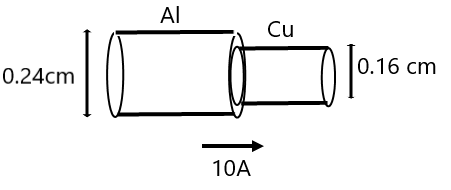
| (1) ज्ञात करें (a) Al के तार में धारा घनत्व (b) ताम्बे के तार में इलेक्ट्रॉनों का अनुगमन वेग जबकि ताम्बे में इलेक्ट्रान घनत्व
(2) एक तार में (3) Cu की किसी तार का अनुप्रस्थ क्षेत्रफल 2 mm² है । इसमें 2A धारा प्रवाहित होती है । तार में इलेक्ट्रान का अनुगमन वेग ज्ञात करें । मान लीजिये प्रति परमाणु केवल एक ही मुक्त इलेक्ट्रान है । दिया है M= 63 ग्राम तथा Cu का घनत्व 8900 kg/m³ है । (
|
ओम का नियम
यदि किसी चालक की भौतिक अवस्थाएं ( ताप , घनत्व इत्यादि ) न बदले तो उसमे से प्रवाहित विधुत धारा, उसके सिरों पर लगाए गए विभवांतर के समानुपाती होता है ।
अर्थात ,
जहाँ R एक नियतांक है जिसे चालक का प्रतिरोध कहते है । इसका S.I मात्रक V/A या ओम होता है ।
दूसरे शब्दों में ओम के नियम के अनुसार ” जब तक किसी चालक की भौतिक अवस्था में कोई परिवर्तन न किया जाये , तब तक उसका प्रतिरोध नियत रहता है , चाहे चालक के बीच कितना ही विभवांतर क्यों न लगाया जाये । ”
ओम के नियम की व्युत्पत्ति

माना की l लम्बाई का एक चालक है जिसका समरूप अनुप्रस्थ क्षेत्रफल A है । माना की चालक के प्रति इकाई आयतन में मुक्त इलेक्ट्रॉन्स की संख्या n है । चालक के सिरों में V विभवांतर आरोपित किया जाता है , जिसके कारण चालक के अंदर समरूप विधुत क्षेत्र E उत्पन्न हो जाता है ।
हम जानते है की इलेक्ट्रान का अनुगमन वेग होगा
जहाँ एक नियतांक है जिसे पदार्थ का प्रतिरोध कहते है इसे R द्वारा सूचित किया जाता है
अर्थात
यह ओम का नियम कहलाता है । S.I पद्दति में R का मात्रक (V/A) या ओम (Ω) होता है ।
प्रतिरोध :- पदार्थ का वह गुण जिसके कारण वह उससे प्रवाहित होने वाली विधुत धारा का विरोध करता है , प्रतिरोध कहलाता है ।
पदार्थ का प्रतिरोधकता
हम जानते है की
जहाँ एक अलग प्रकार का नियतांक है जिसे पदार्थ की प्रतिरोधकता ( विशिष्ट प्रतिरोध ) कहा जाता है । इसका S.I मात्रक
होता है ।
NOTE:-
- प्रतिरोधकता , पदार्थ पर निर्भर करता है लेकिन प्रतिरोध , पदार्थ के साथ साथ चालक की लम्बाई तथा क्षेत्रफल पर निर्भर करता है ।
- जिस चालक का प्रतिरोध मापने योग्य हो उसे प्रतिरोधक कहते है । प्रतिरोध का चिन्ह

- प्रतिरोधकता का व्युत्क्रम पदार्थ की चालकता कहलाती है , इसे
द्वारा सूचित किया जाता है ।
अर्थात चालकता का S.I मात्रक
या mho/m या Siemen(S)/m होता है ।
किसी भी पदार्थ के लिए उसका प्रतिरोधकता तथा चालकता का गुणनफल हमेशा इकाई होता है ।
ओम के नियम का सूक्ष्मदर्शीय रूप
हम जानते है की
जहाँ
विधुत धारा घनत्व
जहाँ पदार्थ की चालकता ( या विशिष्ट चालकता ) है । यह ओम के नियम का सूक्ष्मदर्शीय रूप है ।
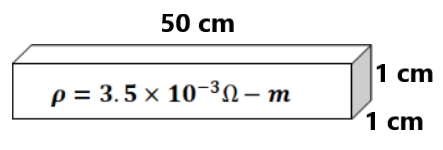
| (1) किसी तार की लम्बाई 2m तथा व्यास 1mm है । इसका प्रतिरोध ज्ञात करें (a) तार के पदार्थ की प्रतिरोधकता (2) एक (3) किसी तार को खींचकर इसका व्यास आधा कर दिया जाता है । इसका नया प्रतिरोध कितना होगा ? (4) यदि कॉपर के तार को 0.3% खिंचा जाता है तो इसके प्रतिरोध में होने वाले प्रतिशत परिवर्तन की गणना करें । (0.6%) (5) किसी तार की लम्बाई दुगुनी तथा अनुप्रस्थ काट क्षेत्रफल आधी कर दी जाये तो निम्न में वृद्धि ज्ञात करें । (a) प्रतिरोध (b) प्रतिरोधकता ( 3 गुणा , none) (6) 0.20 cm व्यास की किसी छड़ में 3A विधुत धारा प्रवाहित होती है । छड़ की लम्बाई 1.5 m तथा सिरों के बीच विभवांतर 40V है । छड़ का प्रतिरोध ज्ञात करें । (7) 1m लम्बे खोखले बेलनाकार चालक का प्रतिरोध ज्ञात कीजिये । बेलन का आतंरिक तथा बाह्य त्रिज्याएँ क्रमशः 1mm तथा 2mm है तथा पदार्थ की प्रतिरोधकता (8) प्रतिरोध ज्ञात करें
(a) गुटके के वर्गाकार सिरों के बीच। |
ओम के नियम के अपवाद :
वे पदार्थ जो ओम के नोयं का सटीकता से पालन करते है , ओमीय चालक (Ohmic Conductor) कहलाते है । जैसे अधिकतर धातुएं ।
वे पदार्थ जो ओम के नियम का सटीकता से पालन नहीं करते है , अनओमीय चालक कहलाते है । जैसे निर्वात नली , अर्धचालक डायोड , ट्रांजिस्टर इत्यादि ।
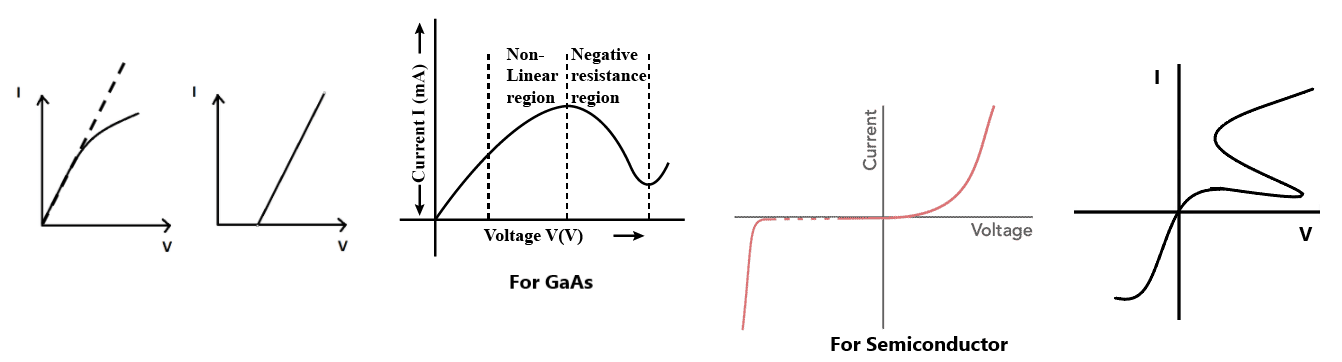
(1) विभवांतर के साथ धारा का परिवर्तन अ- रैखिक ( non linear) होना ।
धात्विक चालक के लिए नियत ताप पर (V-I) ग्राफ खींचे तो एक सरल रेखा प्राप्त होती है , लेकिन धारा की प्रबलता निरंतर बढ़ाये जाने पर चालक का ताप बढ़ता जाता है , जिससे (V-I) ग्राफ सरल रेखा न होकर वक्र हो जाता है ।
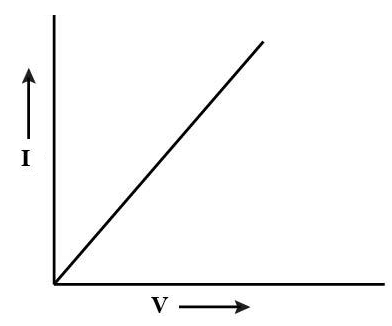
(2) वोल्टता में कमी पर भी धारा में वृद्धि का होना ।
(3) विभवांतर एवं धारा में सम्बन्ध अद्वितीय का न होना ।
(4) केवल एक निश्चित विभवांतर पर ही मापने योग्य धारा का प्रवाहित होना ।
चालकता के पदों में पदार्थों का वर्गीकरण :-
एक आदर्श चालक की चालकता अनंत होती है , जबकि एक आदर्श विधुत रोधी की चालकता शून्य होती है ।
(1) सुचालक :- वे पदार्थ जिनकी चालकता से
की कोटि में होती है , विधुत के सुचालक होते है ।
(2) अर्धचालक :- वे पदार्थ जिनकी चालकता से
की कोटि में होती है , विधुत के सुचालक होते है ।
(3) कुचालक/ विधुत रोधी :- वे पदार्थ जिनकी चालकता से भी कम होती है , विधुत रोधी कहलाते है ।
तापमान के साथ प्रतिरोध / प्रतिरोधकता में परिवर्तन
किसी चालक द्वारा उत्पन्न प्रतिरोध उसमे उपस्थित मुक्त इलेक्ट्रान एवं आयन्स के टक्करों के कारण होता है । जब चालक के ताप में वृद्धि होती है तो टक्करों के बीच का समय कम हो जाता है । अर्थात विधुत धारा का विरोध भी बढ़ जाता है ।
अतः हम कह सकते है की चालकों का प्रतिरोधकता / प्रतिरोध तापमान बढ़ने से बढ़ता है तथा तापमान घटने से घटता है ।
ताप के अल्प मानों के लिए ताप तथा प्रतिरोधकता निम्न सम्बन्ध द्वारा व्यक्त किया जा सकता है ।
जहाँ
प्रारंभिक ताप पर चालक की प्रतिरोधकता
अंतिम ताप पर चालक की प्रतिरोधकता
तापमान में वृद्धि ( तापमान को केल्विन में लेना होगा )
प्रतिरोधकता ताप गुणांक (temperature coefficient of resistivity)
इसका S.I मात्रक /K या /°C होता है ।
हम जानते है की
यदि अल्प तापमान के साथ में कोई परिवर्तन नहीं होता है तो
अर्थात ताप के साथ, प्रतिरोध के लिए हम लिख सकते है
जहाँ प्रतिरोध ताप गुणांक (temperature coefficient of resistivity)
NOTE:-
(a) का मान जितना कम या अधिक होगा , तापमान के साथ प्रतिरोध में वृद्धि उतना ही कम या अधिक होगा ।
(b) चालकों के लिए +ve होता है अर्थात तापमान में वृद्धि के साथ इसका प्रतिरोध बढ़ता है ।
(c) कुचालकों तथा अर्धचालकों के लिए का मान -ve होता है अर्थात ताप के साथ इसका प्रतिरोध घटता है ।
(d) मिश्र धातु (Alloy) जैसे मैगनिन, नाइक्रोम , कान्सटेन्टेन इत्यादि के लिए का मान बहुत ही कम होता है
अर्थात ताप के साथ इसका प्रतिरोध में परिवर्तन बहुत ही कम होता है ।
(e) पर अर्धचालक , कुचालक की तरह व्यवहार करते है , परन्तु कमरे के ताप पर ये चालकों की तरह व्यवहार करते है ।
(f) अर्धचालक या कुचालक के लिए
जहाँ चालक तथा संयोजी बैंड के बीच ऊर्जा अंतराल
वोल्ट्जमैन नियतांक (Boltzmann Constant)
(g) ताप बढ़ने से विधुत अपघट्यों की प्रतिरोधकता कम हो जाती है , क्योंकि विधुत अपघट्य की श्यानता (Viscosity) घट जाती है , जिससे की उसके अंदर आवेश वाहकों को चलने फिरने में पहले से अधिक स्वतंत्रता मिल जाती है ।
अतिचालकता (Superconductivity)
किसी धातु , मिश्रधातु , ऑक्साइड का वह गुण जिसके कारण वह अल्प ताप पर लगभग शून्य प्रतिरोध प्रदर्शित करता है , अति चालकता कहलाती है ।
वे पदार्थ जो अतिचालकता का गुण दर्शाते है अतिचालक कहलाते (super conductor) है । वह तापमान जिसके निचे कोई पदार्थ अतिचालक में परिवर्तित हो जाता है , क्रांतिक तापमान कहलाता है ।
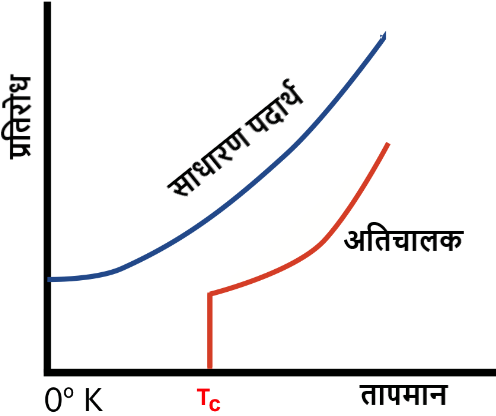
प्रयोग से यह देखा गया है की 4.2 K के निचे Hg का प्रतिरोध घटकर शून्य हो जाता है । किसी अतिचालक में इलेक्ट्रॉन्स परस्पर सम्पूर्ण कला सम्बन्ध रूप से प्रवाहित होते है तथा उनके बीच टक्कर नहीं होती है ।
यदि एक बार अतिचालकता लूप में धरा प्रवाहित कर दी जाती है तो स्विच बंद कर देने के उपरान्त भी धारा अनंत समय तक बने रहते है ।
थर्मिस्टर (Thermister)
थर्मिस्टर वह पदार्थ होता है जिसका प्रतिरोध ताप गुणांक ( ) बहुत ही उच्च होता है । जिसके कारण ताप में अल्प परिवर्तन के साथ थर्मिस्टर का प्रतिरोध बहुत तीव्रता से परिवर्तित होता है । इसमें
+ve तथा -ve दोने हो सकते है ।
साधारणतः थर्मिस्टर अर्धचालक का बना होता है जिसमे -ve होता है ।
उपयोग :-
(a) इसका उपयोग विधुत परिपथ में वाल्ट को नियंत्रण करने में किया जाता है ।
(b) थर्मिस्टर का उपयोग तापमापी यंत्र में भी किया जाता है ।
| (1) 27°C पर किसी प्रतिरोधक का प्रतिरोध 83 Ω है । यदि प्रतिरोध 100 Ω पाया जाये तथा प्रतिरोधक के पदार्थ का ताप गुणांक (2) किसी टंगस्टन की कुंडली का 15 °C पर प्रतिरोध 12 Ω है । यदि टंगस्टन का प्रतिरोधक ताप गुणांक 0.004 /°C हो तो 80 °C पर कुंडली के प्रतिरोध की गणना करें । (15 Ω) (3) किसी तार का 300K पर प्रतिरोध 1 Ω है । किस ताप पर तार का प्रतिरोध 2 Ω हो जायेगा । दिया हुआ है α= 0.00125 /°C . (1127.4 K) (4) टंगस्टन धातु का प्रतिरोधकता ताप गुणांक 0.0045 /°C है , इसके एक तार का 200 °C पर प्रतिरोध 148 Ω है । 0 °C एवं 500 °C पर इसका प्रतिरोध क्या होगा ? ( 77.9 Ω , 253 Ω) (5) चांदी के तार का 0°C पर प्रतिरोध 1.25 Ω है । इसके प्रतिरोध को दुगुना करने के लिए इसे किस ताप पर गर्म करना पड़ेगा ? α= 0.00375 /°स। (267 °C) |
प्रतिरोधकों का संयोजन / समूहन
परिपथ के निर्माण के लिए बहुत से प्रतिरोधकों को एक दूसरे के साथ संयोजित किया जाता है ।
(1) श्रेणी क्रम (Series Connection):-
इस क्रम में सभी प्रतिरोधों को एक ही पथ से जोड़ा जाता है । इसमें सभी प्रतिरोधों में विधुत धारा समान रहती है।
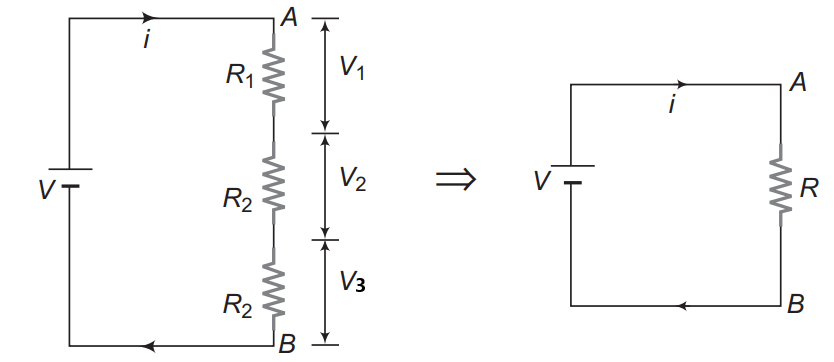
श्रेणी क्रम में प्रतिरोधों में विभव का वितरण होता है । माना की R1 , R2 तथा R3 प्रतिरोधकों के सिरों का विभवांतर V1 , V2 तथा V3 हो तो
हम जानते है की
यदि तथा
का समतुल्य प्रतिरोध
हो तो ,
समीकरण (1) और (2) से
NOTE:-
(a) हम जानते है की
श्रेणी क्रम में अचर है
अर्थात जिसका प्रतिरोध अधिक होगा उसका विभवांतर भी अधिक होगा
(b) दो प्रतिरोध के लिए
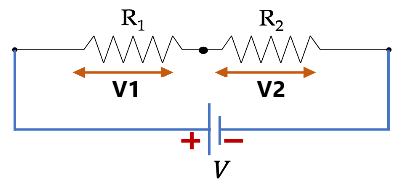
तथा
(c) इस क्रम में समतुल्य प्रतिरोध का मान संयोजन में सबसे बड़े प्रतिरोध के मान से भी बड़ा होता है ।
(2) समान्तर क्रम (Parallel Connection):-
इस क्रम में सभी प्रतिरोधों का एक सिरा एक साथ तथा दूसरा सिरा एक साथ इस प्रकार जोड़ा जाता है की प्रत्येक प्रतिरोधों का विभवांतर समान हो ।
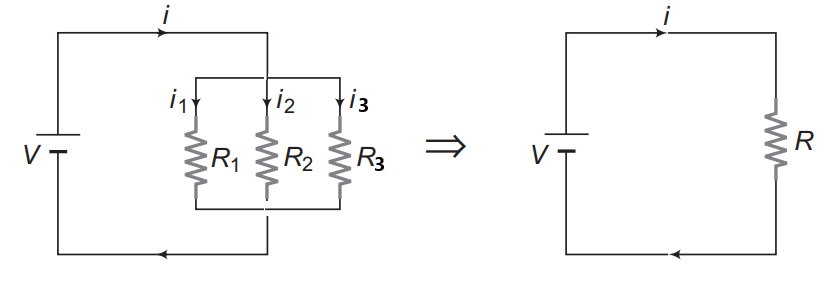
समांतर क्रम में विधुत धारा का वितरण होता है । माना की तथा
में क्रमशः
तथा
विधुत धारा प्रवाहित हो रही है ।
तो सेल से निकलने वाली धारा होगी
हम जानते है की
यदि तथा
का समतुल्य प्रतिरोध
हो तो
समीकरण (1) और (2) से
NOTE:-
(a) हम जानते है की
समांतर क्रम में अचर होता है , अर्थात
अर्थात कम मान वाले प्रतिरोध में अधिक धारा प्रवाहित होगी ।
(b) दो प्रतिरोध के लिए
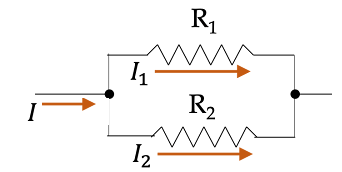
तथा
(c) इस क्रम में समतुल्य प्रतिरोध का मान संयोजन के सबसे छोटे प्रतिरोध के मान से भी कम होता है ।
| sd |