REFRACTION THROUGH A PRISM -

Refraction through prism (introduction)

hhh

PRISM

A prism is a portion of a transparent medium bounded by two plane faces inclined to each other at a suitable angle.

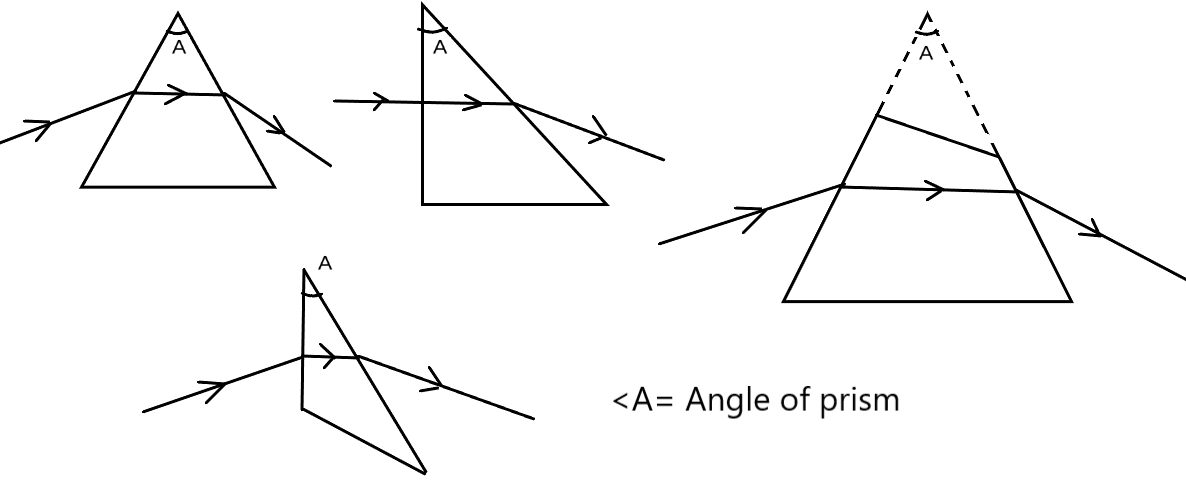
TERM ASSOCIATED IN PRISM

(a) Angle of prism:- The angle of a prism or the refracting angle of a prism is the angle between the plane on which light is incident and the plane from which light emerges.

(b) Incidence angle:- It is the angle that the incident ray makes with the normal to the plane where the ray first strikes the prism.

(c) Emergence Angle:- It is the angle that the ray that emerges out of the prism makes with the normal to the plane where the ray exit the prism.

(d) Angle of deviation:- It is the angle between the emergent ray and the incident ray. Generally, it is denoted by $\fn_cm \large \delta$

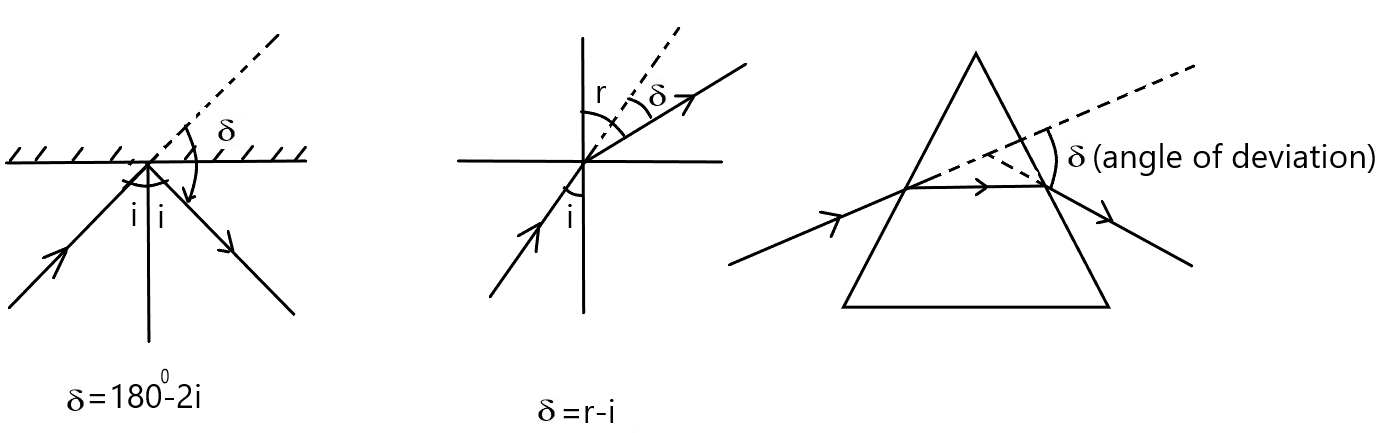
CALCULATION OF ANGLE OF DEVIATION

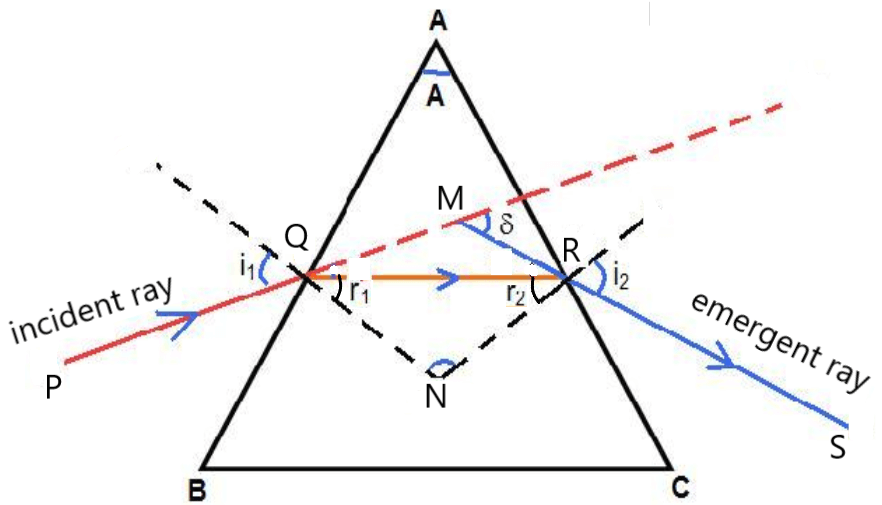
Let ABC is a prism with angle A. A ray of light PQ is incident on the face AB of the prism at an angle $\fn_cm \large i_{1}$ . It bends towards the normal with a refraction angle $\fn_cm \large r_{1}$ . The refracted ray QR is incident at face AC with an angle $\fn_cm \large r_{2}$ . It bends away from normal with a refraction angle $\fn_cm \large i_{2}$ .

From fig. $\fn_cm \large \delta$ is the angle of deviation.

$\fn_cm \large i.e\;in\;\Delta MQR$

$\fn_cm \large \Rightarrow \delta =\angle MQR+\angle MRQ$

$\fn_cm \large \Rightarrow \delta =(i_{1}-r_{1})+(i_{2}-r_{2})$

$\fn_cm \large \Rightarrow \delta =(i_{1}+i_{2})-(r_{1}+r_{2})-----(1)$

$\fn_cm \large in\;\Delta QNR\;\;r_{1}+r_{2}+\angle QNR=180^{0}-----(a)$

In quadrilateral AQNR

$\fn_cm \large \Rightarrow A+\angle AQN+\angle QNR+\angle ARN=360^{0}$

$\fn_cm \large \Rightarrow A+90^{0}+\angle QNR+90^{0}=360^{0}$

$\fn_cm \large \Rightarrow A+\angle QNR=180^{0}-----(b))$

from (a) and (b)

$\fn_cm \large r_{1}+r_{2}+\angle QNR=A+ \angle QNR$

$\fn_cm \large \left [ r_{1}+r_{2}=A \right ]$

from (1)

$\fn_cm \large \left [ \delta =i_{1}+i_{2}-A \right ]-----(A)$

Thus, the angle of deviation depends on the angle of incidence.

Let $\fn_cm \large \mu$ is the refractive index of prism.

using Snell’s law for face AB

$\fn_cm \large \frac{ \sin i_{1}}{sin r_{1}}=\mu$

for small angle

$\fn_cm \large \frac{i_{1}}{r_{1}}=\mu$

$\fn_cm \large \therefore \left [ i_{1}=\mu r_{1} \right ]$

Similarly for face AC

$\fn_cm \large \left [ i_{2}=\mu r_{2} \right ]$

we know that

$\fn_cm \large \delta =i_{1}+i_{2}-A$

$\fn_cm \large \Rightarrow \delta =\mu r_{1}+\mu r_{2}-A$

$\fn_cm \large \Rightarrow \delta =\mu(r_{1}+r_{2})-A$

$\fn_cm \large \Rightarrow \delta =\mu A-A\;\;\;\;\;(\because r_{1}+r_{2}=A)$

$\fn_cm \large \left [ \delta = (\mu -1)A \right ]-----(B)$

NOTE:- When the refracting angle of the prism is small ( $\fn_cm \large < 10^{0}$ ) formula (B) is used for finding the angle of deviation, otherwise formula (A) is used.

PRISM FORMULA

We know that the angle of deviation depends on the angle of incidence (i) as $\fn_cm \large \delta =i_{1}+i_{2}-A$

when i is increased, $\fn_cm \large \delta$ first decreases, reaches a minimum, and increases again.

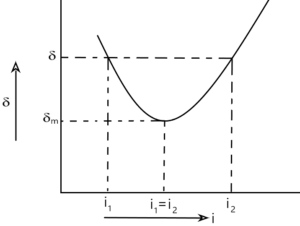
for one value of, there are two angles of incidence $\fn_cm \large i_{1}\;and \;i_{2}$ . This is because “When the direction of the light ray is reversed, the ray simply retraces its path. This statement is called the principle of Reversibility of path of light“

i.e, if the ray is reverse, the angle of incidence is $\fn_cm \large i_{2}$ and angle of emergence is $\fn_cm \large i_{1}$ and then the angle of deviation is the same $\fn_cm \large \delta =i_{2}+i_{1}-A$

in minimum deviation,

$\fn_cm \large \left [ i_{1}=i_{2} \right ]$

$\fn_cm \large let\;i_{1}=i_{2}=i$

$\fn_cm \large and\;r_{1}=r_{2}=r$

we know that

$\fn_cm \large r_{1}+r_{2}=A$

$\fn_cm \large \Rightarrow r+r=A$

$\fn_cm \large \Rightarrow \left [ r=\frac{A}{2} \right ]$

also,

$\fn_cm \large \Rightarrow \delta=i_{1}+i_{2}-A$

$\fn_cm \large \Rightarrow \delta_{m}=i+i-A$

$\fn_cm \large \Rightarrow \delta=2i-A$

$\fn_cm \large \therefore \left [ i=\frac{\delta_{m} +A}{2} \right ]$

using Snell’s law for face AB

$\fn_cm \large \frac{\sin i}{\sin r}=\mu$

$\fn_cm \large \left [ \mu=\frac{\sin (\frac{\delta_{m}+A}{2})}{\sin \frac{A}{2}} \right ]$

This is the prism formula. This is used to determining R.I of the material of the prism.

NOTE:-

1. Angle for maximum deviation:-

we know that $\fn_cm \large \delta =i_{1}+i_{2}-A$

$\fn_cm \large \delta$ is maximum when incidence angle (i) is maximum. And the maximum value of i is $\fn_cm \large i_{max}=90^{0}$

2. Condition for no emergence:-(MAYBE IGNORE THIS PORTION)

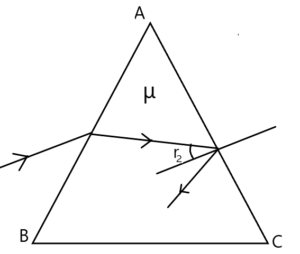
From fig, if the ray does not emerge from face AC, this will happen only when TIR occurs for a glass-air interface.

$\fn_cm \large i.e \;\;r_{2}>\theta _{c}$

$\fn_cm \large now\;\;r_{1}+r_{2}=A$

$\fn_cm \large \Rightarrow r_{2}=A-r_{1}$

$\fn_cm \large \Rightarrow r_{2min}=A-r_{1max}-----(1)$

Now $\fn_cm \large r_{1}$ is maximum when $\fn_cm \large i_{1}$ is maximum and we know that maximum value of $\fn_cm \large i_{1}=90^0$

$\fn_cm \large \Rightarrow \mu =\frac{\sin i_{1max}}{\sin r_{1max}}$

$\fn_cm \large \Rightarrow \mu =\frac{\sin 90^{0}}{\sin r_{1max}}$

$\fn_cm \large \Rightarrow \mu =\frac{1}{\sin r_{1max}}$

$\fn_cm \large \Rightarrow \sin r_{1max}=\frac{1}{\mu }=\sin \theta _{c}\;\;\;\;\; (\because \sin \theta _{c}=\frac{1}{\mu})$

$\fn_cm \large \Rightarrow r_{1max}=\theta _{c}$

from (1)

$\fn_cm \large \Rightarrow r_{2min}=A-\theta _{c}$

Now TIR will happen, when $\fn_cm \large r_2>\theta_{c}$

Obviously, 100% TIR will occur, when $\fn_cm \large r_{2min}>\theta_{c}$

$\fn_cm \large \Rightarrow A-\theta_{c}>\theta_{c}$

$\fn_cm \large \left [ A>2\theta_{c} \right ]$

When the angle of the prism is twice the critical angle for the material of the prism, the emergent angle is totally internally reflected and not emerged out.

RELATED LINK OF RAY OPTICS AND OPTICAL INSTRUMENTS
Introduction	Refraction
Total Internal Reflection	Refraction at Spherical Surfaces and by Lenses
Refraction at Spherical Surfaces and by Lenses	Dispersion by a Prism
Some Natural Phenomena due to Sunlight	Optical Instruments

IMPORTANT QUESTIONS FOR PRACTICE

1. A prism is made of glass of unknown refractive index. A parallel beam of light is incident on the face of the prism. The angle of minimum deviation is measured to be $\fn_cm \large 40^{0}$ . What is the refractive index of the material of the prism? The refracting angle of the prism is $\fn_cm \large 60^0$ . if the prism is placed in water (R.I=1.33), predict the new angle of minimum deviation of a parallel beam of light.