ELECTRIC CHARGES AND COULOMB'S LAW -

ELECTRIC CHARGE:-

Charge is the intrinsic property associated with the matter due to which it produces and experiences electric and magnetic effects. Similarly mass is a property of a body due to which a gravitational field is produced.

Generally, we know that there are only two elementary particles that have electric charge, Electron, and Proton.

Charge of electron= $\fn_cm -1.6\times 10^{-19}C\;(e^{-})$

Charge of proton= $\fn_cm +1.6\times 10^{-19}C\;(e^{+})$

Charge of neutron= $\fn_cm 0$

Mass of electron= $\fn_cm 9.1\times10^{-31}Kg$

Mass of proton= $\fn_cm 1.672\times10^{-27}Kg$

Mass of neutron= $\fn_cm 1.675\times10^{-27}Kg$

In normal conditions, a body contains an equal number of electrons and protons. So the total charge of a body is zero. The body is said to be charged, if the number of electrons and protons are unbalanced (not equal)

A positively charged body has an excess of protons and a shortage of electrons. A negatively charged body has an excess of electrons and a shortage of protons. When we say that a body is charged, we always refer to excess charge on the body.

Electric charge is a scalar quantity. Its S.I unit is Coulomb (C), $\fn_cm 1\;e.s.u=\frac{1}{3\times10^9}C$ , 1 e.m.u= 10C

CONDUCTORS AND INSULATORS: –

In general, the substances are divided into two classes based on their ability to conduct electric charge.

Those substances which have to contain more free electrons at room temperature and due to this electric charge can flow very easily on them are called conductors. Ex- silver, copper, aluminum, etc.

Those substances which have no free electrons at room temperature and electric charge cannot flow easily on them are called insulators. Ex- glass, rubber, mica, etc.

NOTE: –

When some charges are given to the conductor, they readily get distributed over the entire surface of the conductor. In contrast, if some charges are put on an insulator, it stays nearby at the same place

FRICTIONAL ELECTRICITY: –

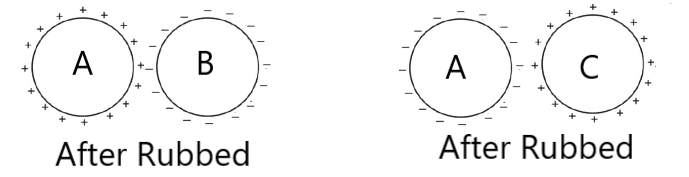
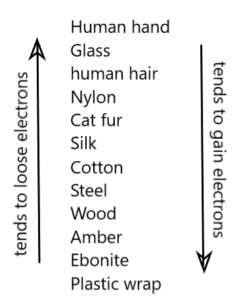
It is the electricity produced by rubbing two suitable bodies (insulators) and the transfer of electrons from one body to the other.

The body which loses the free electrons becomes +ve charged while the body which receives the free electrons, becomes –ve charged.

NOTE: –

1. In charging only free electrons are transferred from one body to another.
2. During charging mass is also affected.
3. In electrolyte (liquid) both –ve and +ve ions are mobile.

EARTHING AND GROUNDING: –

(basic idea which is given in this chapter of NCERT)

when we bring a charged body in contact with the earth, all the excess charge on the body disappears by causing momentary current to pass to the ground through the connecting low resistance conductor. This process of sharing the excess charge with the earth is called grounding or earthing.

Earthing provides a safety measure for electrical circuits and appliances. In earthing charges may be transferred from body to earth or earth to the body.

(You will get it from the details concept in the electric potential chapter)

GOLD LEAF ELECTROSCOPE: –

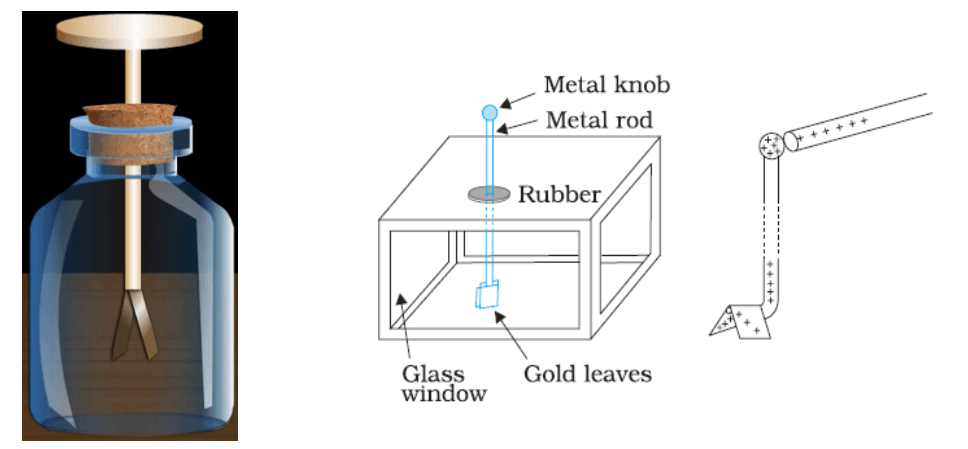
It is a simple apparatus to detect charges on a body. It consists of a verticle metal rod housed in a box, with two thin gold leaves attached to its bottom end. When a charged object touches the metal knob at the top of the rod, charges flow onto the leaves and they diverge. The degree of divergence is an indicator of the amount of charge.

METHODS OF CHARGING OF A BODY: –

An uncharged body can be charged by the following three methods.

1> By friction: – discussed earlier

2>By conduction/contact: – in this method, a charged body is brought in contact with the uncharged conductor. In this case, electrons from one body would be transferred to the other.

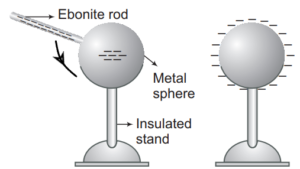
3>By Induction: –In this method, a charged body is brought close to the uncharged conductor but does not contact with it

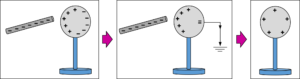
NOTE: –

By induction process, a charged body attracts an uncharged body placed nearby. So we can say that attraction is not proof of bodies being charged. But repulsion shows on the charged body.

PROPERTIES OF ELECTRIC CHARGE: –

1>Charge is transferable.

2>Charge is always associated with mass.

3>Chare produces electric and magnetic field.

4>Charge is independent of velocity.

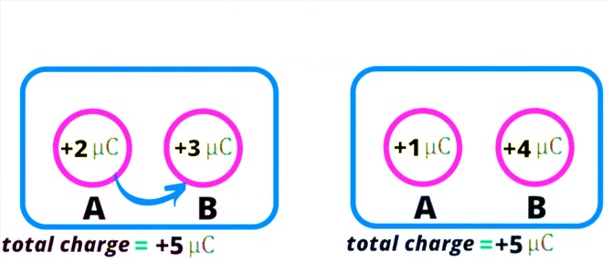
5>Additivity of charge: – the total electric charge of a body (or system) is equal to the algebraic sum of all the individual charges located at different parts of the body.

6>Quantization of electric charge: –According to this the total charge of a body is integral multiple of quantum of charge (Charge of an electron)

i.e. $\fn_cm \left [ Q=\pm ne \right ]\;\;where\;n=0,1,2,3.....$

7> Conservation of charge: – According to this the total charge of an isolated system always remains conserved.

NOTE:-

1. Charge on anybody can never be $\fn_cm \left ( 1.5e,\frac{1}{3}e \right )$ , etc
2. Apart from charge, energy (hf), angular momentum (h/2π) is also quantized.
3. Recent discoveries in high energy physics have indicated that elementary particles like protons and neutrons are themselves built out of more elementary units, called quarks, which have charge (2/3)e and (-1/3)e. Even if the quark model is established in the future, the quantization of charge will still hold. Only the quantum of charge will reduce from e to e/3.

Question> Can two similar charged bodies attract each other?

Ans> Yes, when the charge on one body (say Q1) is much greater than that on the other (say Q2) and they are close enough to each other so that the force of attraction between Q1 and the induced charge on the other exceeds the force of repulsion between Q1 and Q2.

Question> Why does a charged comb attract a small piece of paper which is uncharged?

QUESTIONS RELATED TO THE CHARGE

Q.1. A glass rod is rubbed with silk cloth. The glass rod acquires a charge of $\fn_cm +19.2\times10^{-19}C$ .

Find (a) Find the number of electrons lost by the glass (b) Find the -ve charge acquired by silk. (c) Is there a transfer of mass from glass to silk?

Q.2. Calculate the number of electrons in 250 grams of water.

Q.3. How many electrons should be removed from a body to acquire +3.2μC charge on a body?

Q.4. How many electrons contain in -1C charge?

Q.5. Is charge 0f $\fn_cm 4.5\times10^{-19}C$ possible?

Q.6. If $\fn_cm 10^9$ electrons move out of a body to another body every second. How much time (years) is required to get a total charge of 1C on the other body?

Q.7. What will happen if B and C are Rubbed?

Q.8. Object A, B, and C are three identical insulated spherical conductors. Initially, A and B have a charge of +3 μC whereas C has a charge of -6μC. Object A and C are touched and moved apart. Objects B and C are touched before they are moved apart.

(a) If objects A and B are now held near each other, they will (a) attract (b) repel (c) have no effect

(b) If A and C are held near each other they will (a) attract (b) repel (c) have no effect

Q.9.

(a) What would happen if the rod is removed before the spheres are separated?

(b) Would the induced charges be equal in magnitude even if the spheres had different sizes or different conductors?

Q.10. Calculate the total +ve (or -ve) charge on a 3.11 gram Cu Penny. (Given atomic no=29, atomic mass 63.5g)

Q.11. (a) Can two bodies having like charges attract each other?

(b) Can a charged body attract an uncharged body?

(c) Two identical metallic spheres of exactly equal masses are taken, one is given a +ve charge q and the other an equal -ve charge. Are there masses after charging differently?

Q.12. In 1 gram of a solid, there are $\fn_cm 5\times10^{21}$ atoms . If one electron is removed from each of 0.01 % atoms of the solid, find the charge gained by the solid.

COULOMB’S LAW: –

According to this, the electrostatic force between two stationary point charges is directly proportional to the product of their magnitudes and inversely proportional to the square of the distance between them and acting along the line joining the two charges.

$\fn_cm F\propto Q_1Q_2\;\;\;------(1)$

$\fn_cm F\propto \frac{1}{r^2}\;\;\;------(1)$

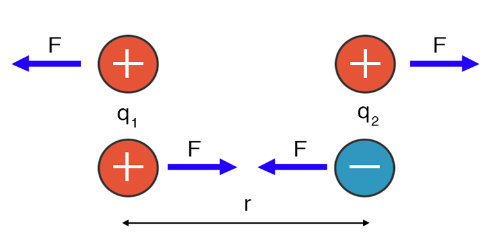
From equation (1) and (2)

$\fn_cm \left [ F\propto \frac{Q_1Q_2}{r^2} \right ]$ (Inverse square law)

$\fn_cm \left [ F= k\frac{Q_1Q_2}{r^2} \right ]$

Where k is the constant known as the electrostatic force constant and its value depends upon the nature of the medium between them.

When the charges are situated in free space (air/ vacuum), then in the S.I unit, the value of k is

$\fn_cm \left [ k=\frac{1}{4\pi\epsilon_0} \right ]$

where $\fn_cm \epsilon_0$ is called the absolute permittivity of free space and its value is $\fn_cm \left ( \epsilon_0=8.854\times10^{-12}C^2/Nm^2 \right )$

NOTE:-

(1) Permittivity is the electrical property of the medium. It is also the inverse degree of permission of the medium. It means that the inverse degree of permission has to be minimum if the charge present in a vacuum. As the charges are free to interact in a vacuum. It is also a measure of the degree of the medium which resist the flow of charge.

$\fn_cm k=\frac{1}{4\pi\epsilon_0}=\frac{1}{4\times3.14\times8.854\times10^{-12}}$

$\fn_cm \left [ k\approx 9\times10^9 \;Nm^2/C^2 \right ]$

i.e. we can write for free space

$\fn_cm \left [ F=\frac{kQ_1Q_2}{r^2}=\frac{1}{4\pi\epsilon_0}.\frac{Q_1Q_2}{r^2} \right ]$

if we put $\fn_cm Q_1=Q_2=1C\;\;and\;\;r=1m$ then we get $\fn_cm \left [ F=9\times10^9N \right ]$

i.e. ” 1C is the charge that, when placed at a distance of 1m from another charge of the same magnitude in vacuum experiences an electric force of repulsion of magnitude $\fn_cm 9\times10^9N$ . “

(2) For any medium:-

$\fn_cm \left [ F_m=\frac{1}{4\pi\epsilon_m}.\frac{Q_1Q_2}{r^2} \right ]$

Where $\fn_cm \varepsilon _m$ is the absolute permittivity of the medium.The absolute permittivity of all other mediums is greater than $\fn_cm \epsilon_0$

(3) DIELECTRIC CONSTANT (Relative Permittivity): –Relative permittivity of the medium is the permittivity of the medium with respect to the permittivity of free space/vacuum.

i.e. $\fn_cm \left [ \epsilon_r=\frac{\epsilon_m}{\epsilon_0} \right ]$

For air $\fn_cm F_{air}=\frac{1}{4\pi\epsilon_0}.\frac{Q_1Q_2}{r^2}-----(1)$

For medium $\fn_cm F_m=\frac{1}{4\pi\epsilon_m}.\frac{Q_1Q_2}{r^2}-----(2)$

From equation (1) and (2)

$\fn_cm \left [ \frac{F_{air}}{F_m}=\frac{\epsilon_m}{\epsilon_0}=K(dielectric \; constant) \right ]$

For vacuum or air K=1

For good conductors like metal K=∞

NOTE: –

The introduction of a glass slab between two charges will decrease (due to polarization) the magnitude of the force between them.
The introduction of a metallic slab between two charges will decrease the magnitude of force to zero.
Coulomb’s law is valid at a distance greater than
The electric force is conservative in nature.

ELECTROSTATIC FORCE vs GRAVITATIONAL FORCES

Electrostatic force is the force of attraction or repulsion between two charges at rest while the gravitational force is the force of attraction between two bodies by virtue of their masses.

Similarities:

Both forces obey inverse square law i.e $\fn_cm F\propto 1/r^2$
Both forces are proportional to the product of masses or charges.
Both are central forces i.e., they act along the line joining the centres of the two bodies.
Both are conservative forces i.e., the work done against these forces does not depend upon the path followed.

Dissimilarities:

Gravitational force is attractive while electrostatic force may be attractive or repulsive.
Gravitational force does not depend on the nature of the medium while electrostatic force depends on the nature of the medium between the two charges.
Electrostatic forces are much stronger than gravitational forces.

SUPERPOSITION PRINCIPLE (Force between multiple charges): –

when many charges are present, the total force on a given charge is equal to the vector sum of the forces due to the remaining charges on the given charge.

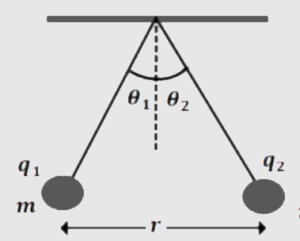
QUESTIONS RELATED TO COULOMB’S LAW

Q.1. A small sphere is given a charge of +20μC and a second sphere of equal diameter is given a charge of -5μC. The two spheres are allowed to touch each other and then separated 10 cm apart. Assume air as the medium, what force exits between them?

Q.2. A charge q is placed at the center of the line joining the two charges of each magnitude Q. Prove that the system of three charges will be in equilibrium if q=-Q/4.

Q.3. The two identical spheres A and B are situated some distance apart. Each has a charge +q coulomb and they repel each other with a force of $\fn_cm 10^{-5}N$ . A third identical conducting sphere C is first touched with A and then with B and then placed exactly midway between A and B. Find the resultant force on C.

Q.4. (a) Two point charges +Q and +4Q are placed at a distance of 9 cm apart on a horizontal plane. Where should the third charge be placed for it to be in equilibrium? (b) Situation are the same but the charges are Q and -4Q and the test charge is +ve.

Q.5. Three point charges of +5μC each are placed at the vertices of an equilateral triangle of side 10 cm long. Find the force on each charge.

Q.6. Two small spheres, each having a mass of 0.1 gare suspended from a point of thread 20 cm long. They are equally charged and they repel each other to a distance of 24 cm. What is the charge on each sphere?

Q.7. The electric force of repulsion between two +vely charged ions carrying equal charge is $\fn_cm 3.7\times10^{-9}N$ when they are separated by a distance of 5Å. How many electrons are missing from each ion?

Q.8. Two small spheres of charge Q are suspended by two insulating strings of equal length ‘ l ‘ from a common point. The system is in place in a gravity-free hall. Find the tension in the string.

Q.9. charges q1 and q2 lie on the x-axis at points x=-4 cm and x=+4 cm respectively. How must q1 and q2 be related so that net electric force on a charge placed at x=+2 cm is zero?

Q.10. Consider the charge q, q, and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge? and find the sum of forces acting on each charge.

Q.11. A particle of mass m carrying a charge -q1 is moving around a fixed charge +q2 along a circular path of radius r. Find the period of revolution of charge q1.

Q.12. Two identical simple pendulums A and B suspended from the same point have charge +q1 and q2 (q1>q2). The pendulums are in equilibrium making an angle θ1 and θ2 with the vertical as shown in Fig. The separation between the point charges is r as shown and the mass of each bob is m. Find (a) angle θ1 and θ2 (b) tension in each string.

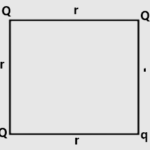
Q.13. A point charge q is kept at the vertices of a square of side r as shown in Fig. Find the force on the charge q.

Q.14. Find the force on charge q as shown in Fig.

Q.15. Find the force on charge q due to charge Q kept at four vertices of a regular pentagon. $\fn_cm \left [ interior \;angle\;of\;polygon=\frac{(n-2)\times180^0}{n} \right ]$

Q.16.

Where should charge q be placed along the line joining so that it is in equilibrium? If charge q is +ve, determine the nature of equilibrium, when

(a) Charge q is displaced slightly along the line joining the two-point charges.

(b) Charge q is displaced slightly along the line perpendicular to the line joining.

(c) If charge q is -ve, discuss the nature of equilibrium in cases (a) and (b) from the above question.

Q.17. Two charged particles A and B, each having a charge Q are placed a distance r apart. Where should a third particle of charge q be placed on the perpendicular bisector of AB so that it experiences maximum force? Also, find the magnitude of the maximum force.

Q.18. From the previous question q is -ve and if it is displaced through a distance x (x<<r) perpendicular to AB and released. Then find the period of the oscillation.

Q.19. Find the acceleration of electron and proton due to the electrical force of their mutual attraction when they are 1Å apart.

Q.20. Two identical conducting spheres 1 and 2 carry equal amounts of charge and are fixed apart at a certain distance larger than their diameters. The spheres repel each other with an electrical force of 88 mN. A third identical sphere 3, having an insulating handle and initially uncharged, is touched first to sphere 1 and then to sphere 2 and finally removed. Find the force between spheres 1 and 2.

Q.21. Three charges of equal magnitude q are placed at the vertices of an equilateral triangle of side l. How can the system of charges be placed in equilibrium?

Q.22. A charge Q is to be divided into two objects. What should be the value of the charges on the objects so that the force between the objects can be maximum?

Q.23. Three particles, each of mass m and carrying a charge q each, are suspended from a common point by insulating massless string, each of length l. If the particles are in equilibrium and are located at the corners of an equilateral triangle of side a, calculate the charge q on each particle, assume l>>>a.

QUESTIONS RELATED TO RELATIVE PERMITTIVITY/DIELECTRIC CONSTANT

Q.1. Calculate the force between two charges each of 20μC in a medium of relative permittivity 4. The distance between the two charges is 40 cm.

Q.2. Suppose two point charges are placed at a distance $\fn_cm r_0$ in a vacuum. Find the distance between these points’ charges when charges are placed in a medium of dielectric constant K, such that the forces experienced are the same.

Q.3. The force between two point charges when placed in free space is 5 N. If they are in a medium of relative permittivity 5, then find the force between them in the medium.

Q.4. Two point charges each of 100 μC are separated in a medium of relative permittivity 2 by a distance of 5 cm. Find the force between them.

Q.5. Find the relative permittivity in both cases.

Q.6. Two charge particles +3 μC and -2μC are placed 2m apart. Half of the region between them is filled with a medium having relative permittivity 9. Find the electric force between two charges.

COULOMB’S LAW IN VECTOR FORM: –

Let the position vector of charge $\fn_cm q_1$ and $\fn_cm q_2$ be $\fn_cm \vec{r}_1$ and $\fn_cm \vec{r}_2$ respectively.

now, $\fn_cm \vec{F}_{12}$ = force on $\fn_cm q_1$ due to $\fn_cm q_2$
$\fn_cm \vec{F}_{21}$ =force on $\fn_cm q_2$ due to $\fn_cm q_1$
$\fn_cm \vec{r}_{21}=\vec{r}_2 -\vec{r}_1=$ distance between charges leading from $\fn_cm q_1$ to $\fn_cm q_2$
$\fn_cm \vec{r}_{12}=\vec{r}_1 -\vec{r}_2=$ distance between charges leading from $\fn_cm q_2$ to $\fn_cm q_1$

$\fn_cm \hat{r}_{21}=\frac{\vec{r}_{21}}{r}=$ unit vector from $\fn_cm q_1$ to $\fn_cm q_2$
and $\fn_cm \hat{r}_{12}=\frac{\vec{r}_{12}}{r}=$ unit vector from $\fn_cm q_2$ to $\fn_cm q_1$

coulomb’s force law between two point charges $\fn_cm q_1$ and $\fn_cm q_2$ located at the position vector $\fn_cm \vec{r}_1$ and $\fn_cm \vec{r}_2$ is then expressed as
Force on $\fn_cm q_2$ by $\fn_cm q_1$ is

$\fn_cm \vec{F}_{21}=\frac{1}{4\pi\epsilon_0}\frac{q_1 q_2}{r^2}\;\hat{r}_{21}$
and force on $\fn_cm q_1$ by $\fn_cm q_2$ is

$\fn_cm \vec{F}_{12}=\frac{1}{4\pi\epsilon_0}\frac{q_1 q_2}{r^2}\;\hat{r}_{12}$

QUESTIONS RELATED TO COULOMB’S LAW IN VECTOR FORM

1. Find the force on charge q kept at (2,3,4) due to charge Q kept at (5,3,8) in vector form.

2. Same as question 1 but q kept at origin and Q kept at (5,3,2)

3. Same as the previous question but q kept at (-1,2,-3) and Q kept at (-3,-2,2).

4. Find the force on the charge Q kept at (5,8,3) due to charge q kept at (2,-3,4) in vector form.

5. A charged particle $\fn_cm q_1$ is at position (2,-1,3). Find the electric force on another charged particle $\fn_cm q_2$ at (0,0,0) in vector form.

6. Find the force on a charge $\fn_cm q_1=20\mu C$ due to the charge $\fn_cm q_2=-10\mu C$ if the position of the charges are given as P(1,-1,2) and Q(-1,1,1)

VERY SHORT ANSWER QUESTIONS