गति के नियम

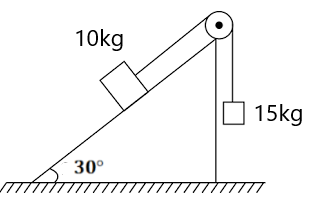
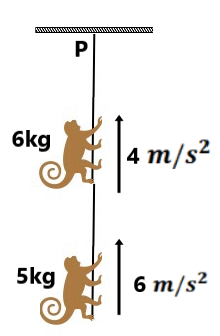
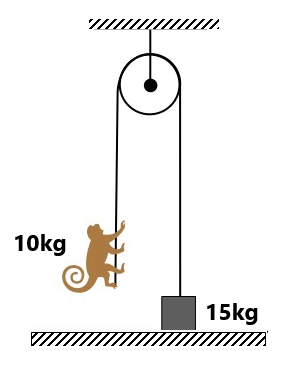
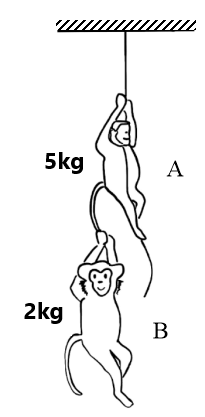
बल ( धक्का या खिंचाव ):-

बल वह भौतिक करक है जो रुके हुए पिंड को गति प्रदान करता है तथा गतिमान पिंड को रोकता है या मंदित करता है।  दूसरे शब्दों में हम यह कह सकते है की बल वह भौतिक करक है जिससे पिंड अपनी अवस्था में परिवर्तन करता है।

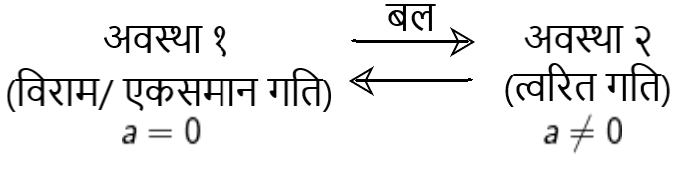
अरस्तू की भ्रामकता  :-

अरस्तू ने गति का नियम दिया कि किसी पिण्ड को गतिशील रखने के लिए बाह्य बल की आवश्यकता होती है। उदाहरण के लिए, किसी धनुष से छोड़ा गया तीर उड़ता रहता है, क्योंकि तीर के पीछे की वायु उसे धकेलती रहती है, जबकि वास्तव में ऐसा नहीं होता है। इसी प्रकार किसी खिलौना गाड़ी को निरंतर चलाने के लिए उसे डोरी से खींचते रहना पड़ता है।

अरस्तू का गति का यह नियम दोषपूर्ण है। इसे ही अरस्तू की भ्रामकता कहते हैं। गैलीलियो ने अपने प्रयोगों के आधार पर इस भ्रामकता को दूर किया तथा जड़त्व का नियम दिया। गैलीलियो ने बताया कि प्रकृति में सदैव ही विरोधी घर्षण बल (ठोसों के बीच) अथवा श्यान बल (तरलों के बीच) आदि उपस्थित रहते हैं जो गति का विरोध करते हैं। इसीलिए हमें वस्तुओं में एकसमान गति बनाए रखने के लिए घर्षण बलों को निष्फल करने हेतु बाह्य साधनों द्वारा बल लगाना आवश्यक होता है।

संपर्क बल-

जब बल लगाने वाली वस्तु, जिस वस्तु पर बल लगाया जा रहा है, उसके संपर्क में हो तो ऐसा बल ‘‘संपर्क बल’’ कहलाता है।

उदाहरण- फुटबाल को गति प्रदान करने के लिए उस पर अवश्य ठोकर मारना, पवन द्वारा पेड़ की शाखाओं को झुलाना, लुढ़कती गेंद को उसकी गति की विपरीत दिशा में बल लगाकर रोकना आदि।

असंपर्क बल-

जिस वस्तु पर बल लगाया जा रहा है, बल लगाने वाली वस्तु से उसका कोई संपर्क नहीं हो तो ऐसा बल ‘‘असंपर्क बल’’ कहलाता है।

उदाहरण- किसी भवन के शिखर से बिना अधोमुखी धक्का दिये मुक्त किया गया पत्थर पृथ्वी के गुरुत्वीय खिंचाव के कारण त्वरित होता है (गुरूत्वाकर्षण बल), कोई छड़ चुंबक लोहे की कीलों को दूर से ही, अपनी ओर आकर्षित कर लेता है (चुंबकीय बल), आवेशों के बीच आकर्षण या प्रतिकर्षण बल।

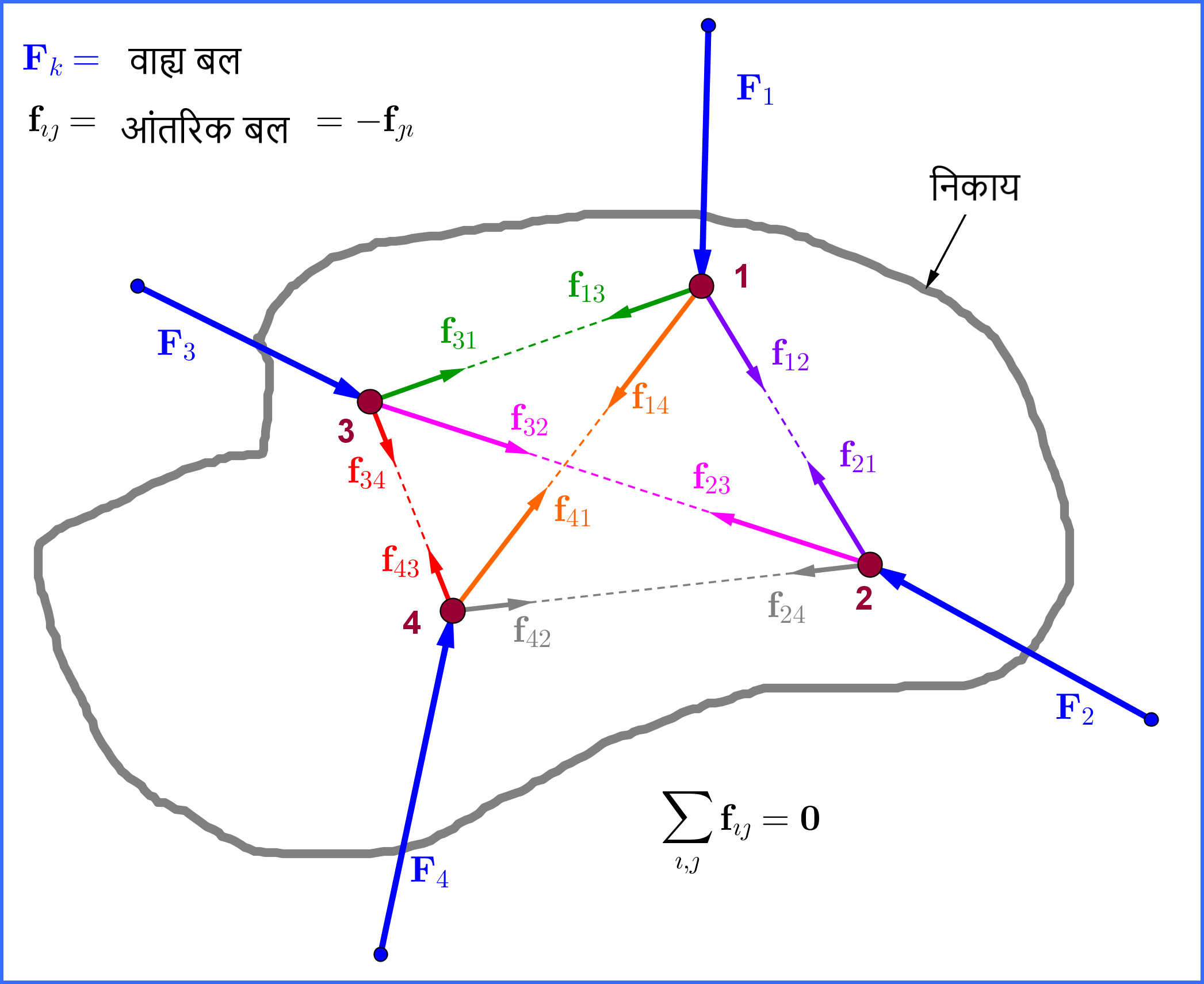
किसी निकाय में लगने वाला आंतरिक तथा वाह्य बल :-

किसी निकाय का एक भाग उसी निकाय के दूसरे भाग पर जो बल आरोपित करता है , उसे आंतरिक बल कहते है।  जैसे परमाणु में नाभिक और इलेक्ट्रान के बिच लगने वाला बल।

यदि निकाय पर बाहर से कोई बल नहीं लगता है तो उसे विलगित निकाय (Isolated system) कहते है।

यदि निकाय पर वाह्य प्रभावों के कारण कुछ अतिरिक्त बल लगता है , तो इस बल को वाह्य बल कहते है।

जड़त्व :-

जड़त्व से तात्पर्य है- ”परिवर्तन के प्रति प्रतिरोध”। वस्तु द्वारा अपनी गति में परिवर्तन का विरोध किया जाता है, वस्तु के इस गुण को जड़त्व कहते है।

अर्थात, वस्तुओं का वह गुण जिसके कारण वह अपनी विरामावस्था या समरूप वेग की अवस्था में परिवर्तन का विरोध करती है जड़त्व कहलाती है।

विराम – स्थिर जड़त्व के कारण

गति – गतिज जड़त्व के कारण

जड़त्व के उदाहरण:

(1) कंबल को छड़ से पीटने पर धूल के कण झड़ जाते हैं।

(2) पेड़ को हिलाने पर उसपर लगे फल गिरने लगते हैं।

(3) मोटर कार के एकाएक चलने पर उसमे बैठा व्यक्ति पीछे की ओर झुक जाता है।

(4) लंबी कूद के खिलाड़ी कुछ दूर पहले दौड़कर छलांग लगाते हैं।

(5) चलते वाहन में एकाएक ब्रेक लगाने पर उसमे बैठा व्यक्ति आगे की ओर झुक जाता है।

NOTE:- स्थानांतरण गति में वस्तु का द्रव्यमान ही वस्तु के जड़त्व के समानुपाती होता है।

 

न्यूटन ने गैलीलिओ की धारणाओं के आधार पर गति के तीन नियम दिए

न्यूटन का गति का प्रथम नियम :-

गैलीलिओ का जड़त्व का नियम उसका आरम्भ बिंदु था जिसका न्यूटन ने ‘ गति के प्रथम नियम ‘ के रूप में संरूपण किया।

“कोई वस्तु अपनी विरामावास्था या समरूप गति में तब तक रहती है, जब तक नेट बाह्य बल (external force) द्वारा उसकी विरामावस्था या गत्याव्स्था में कोई परिवर्तन न लाया जाए”

अर्थात यदि नेट वाह्य बल शून्य है तो विराम अवस्था में रह रहा पिंड विरामावस्था में ही रहता है और गतिशील पिंड निरंतर एकसमान वेग से गतिशील रहता है।  वस्तु के इस गुण को ही तो जड़त्व कहते है अर्थात न्यूटन के प्रथम नियम को जड़त्व का नियम भी कहते है।

विरामावस्था अथवा सरल रेखा में एकसमान गति दोनों ही अवस्थाओं में त्वरण शून्य होता है। अतः गति के प्रथम नियम को, सरल शब्दों में, इस प्रकार भी व्यक्त किया जा सकता है:

यदि किसी पिण्ड पर लगने वाला नेट बाह्य बल शून्य है, तो उसका त्वरण शून्य होता है। पिंड में त्वरण केवल तभी हो सकता है जब पिंड पर कोई नेट बाह्य बल लगता हो।

संवेग :-

किसी पिंड में उसकी गति की कुल मात्रा को संवेग कहते है तथा इसका मान पिंड के द्रव्यमान और उसके वेग के गुणनफल से की जाती है।

इसे P द्वारा सूचित किया जाता है।

  अर्थात     \dpi{120} \fn_cm \left [ \vec{p}=m\vec{v} \right ]

इसका S.I  मात्रक kg m/s  होता है , यह एक सदिश राशि है।

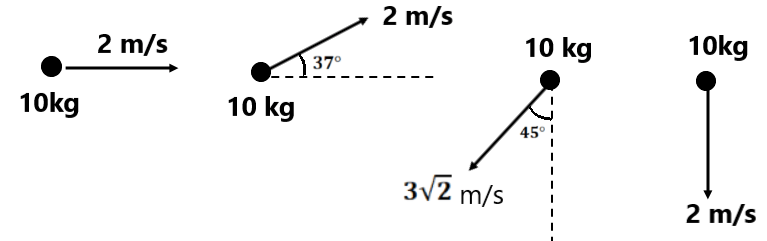
संख्यात्मक प्रश्न

(1) चित्र में वस्तु का संवेग ज्ञात करे तथा उसे सदिश के रूप में व्यक्त करें ।

(2) वस्तु का संवेग में परिवर्तन ज्ञात करे ( मान तथा दिशा )

न्यूटन के गति का द्वितीय नियम :-

किसी पिंड के संवेग परिवर्तन की दर उसमे लगते हुए आरोपित बल के समानुपाती होती है तथा यह परिवर्तन उसी दिशा में होती है जिस दिशा में बल कार्य करता है।  अर्थात

\dpi{120} \fn_cm \left [ \vec{F}\propto \frac{\Delta\vec{P}}{\Delta t} \right ]

माना की m द्रव्यमान का एक वस्तु v वेग से गतिमान है , यदि उसपर F बल जाए तो माना की dt समय में उसका वेग v से v+dv हो जाता है |

अल्प समय के लिए    \dpi{120} \fn_cm \Delta t\rightarrow 0

\dpi{120} \fn_cm \vec{F}\propto \frac{d\vec{P}}{dt}

\dpi{120} \fn_cm \Rightarrow \vec{F}=k \frac{d \vec{P}}{dt}

जहाँ K एक नियतांक है|

\dpi{120} \fn_cm \Rightarrow \vec{F}=k \frac{d(m\vec{v})}{dt}

\dpi{120} \fn_cm \Rightarrow \vec{F}=k \;m \frac{d(\vec{v})}{dt}

\dpi{120} \fn_cm \Rightarrow \vec{F}=k\;m\vec{a}\;\;\;\;\;\left ( a=\frac{dv}{dt} \right )

प्रयोग से k=1

\dpi{120} \fn_cm \left [ \vec{F}=m\vec{a} \right ]

बल एक सदिश राशि है तथा इसका S.I मात्रक \dpi{120} \fn_cm kg\;m/s^2 या Newton (N) होता है। बल का C.G.S मात्रक \dpi{120} \fn_cm g\;cm/s^2 या Dyne होता है।

\dpi{120} \fn_cm 1N=10^5 Dyne

बल का एक प्रचलित मात्रक Kgf होता है , जिसे बल का गुरुत्वीय मात्रक कहते है ।  1 Kgf = 9.8N

NOTE:-

  1. 1 N बल का वह परिमाण है जो 1 kg  के पिंड में \dpi{120} \fn_cm 1\;m/s^2 का त्वरण उत्पन्न कर देता है।
  2. गति के द्वितीय नियम में F=0 से यह प्राप्त होता है की a=0। अतः प्रत्यक्ष रूप से द्वितीय नियम प्रथम नियम के अनुरूप है|
  3. \dpi{120} \fn_cm \Rightarrow \vec{F}=m\vec{a}

\dpi{120} \fn_cm \Rightarrow (\vec{F_x} +\vec{F_y}+\vec{F_z})=m (\vec{a_x} +\vec{a_y}+\vec{a_z})

अर्थात

\dpi{120} \fn_cm \vec{F}_x=m\vec{a}_x\;\;,\;\;\vec{F}_y=m\vec{a}_y\;\;,\;\;\vec{F}_z=m\vec{a}_z

4.  किसी भी  निकाय के लिए कुल आंतरिक बलों का योग शून्य होता है अर्थात F=ma   में केवल कुल वाह्य बलों को ही सम्मिलित किया जाता है  \dpi{120} \fn_cm \vec{F}_{ext}=m\vec{a}_{com}
जैसा की हम जानते है की बल केवल संवेग परवर्तन पर ही निर्भर नहीं करता है , वह इस बात पर भी निर्भर करता है कि कितनी तीव्रता से यह परिवर्तन किया जाता है।   \dpi{120} \fn_cm F=\frac{dp}{dt}

  1. क्रिकेट के खेल में गेंद पकड़ते समय खिलाड़ी अपने हाथ को पीछे कि तरफ खींचता है ,क्योंकि ऐसा करने से उसे गेंद को शून्य संवेग लाने में अधिक समय लगता है , जिसके कारण हाथों में चोट कम लगती है।
  2. ऊंचाई से पक्के फर्श पर कूदने पर अधिक चोट लगती है , जबकि रेत पर कूदने पर अधिक चोट नहीं लगती है।
  3. गाड़ियों में झटकों से बचने के लिए पहिये में स्प्रिंग लगाया जाता है।

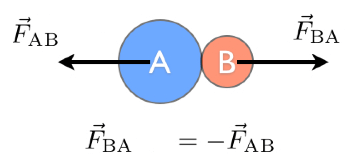
न्यूटन के गति का तृतीय नियम :-

प्रत्येक क्रिया बल कि एक प्रतिक्रिया बल होती है, जिसका मान आपस में समान तथा दिशा एक दूसरे के विपरीत होती है।

 

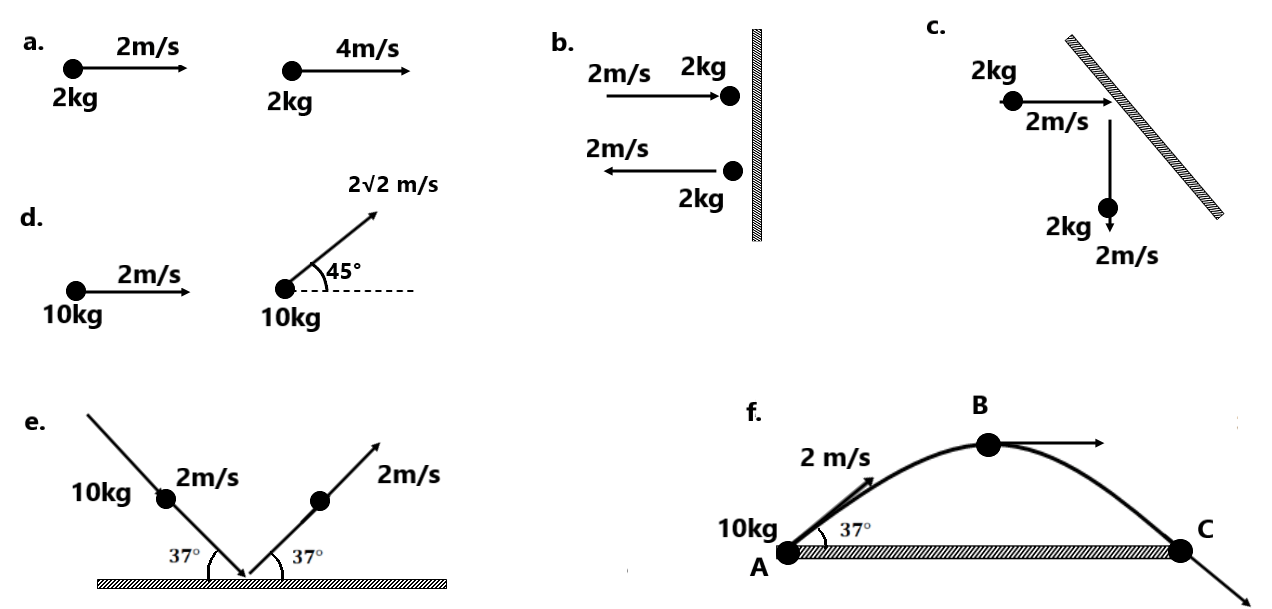
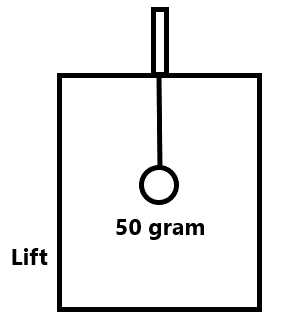
संख्यात्मक प्रश्न 

(1) 5 किलोग्राम द्रव्यमान पर 1 न्यूटन का बल लगाया जाता है । यदि यह विरामावस्था से गति प्रारम्भ करे तो द्रव्यमान द्वारा 10 सेकंड में तय की गई दुरी कितनी होगी ? (10 मीटर )

(2) 50 gram द्रव्यमान का पत्थर ऊर्ध्वाधर ऊपर की ओर फेंका जाता है । पत्थर पर परिणामी बल तथा दिशा ज्ञात कीजिये

(a) गति के दौरान ऊपर की दिशा में
(b) गति के दौरान निचे की दिशा में
(c) उच्चतम बिंदु पर जब वस्तु क्षणिक विरामावस्था में है
(d) यदि पत्थर को क्षैतिज से 45° का कोण बनाते हुए फेंका जाये तो (a) ,(b) तथा (c) की स्थिति में बल का परिमाण ज्ञात करें ।

(3) 72 N का एक बल क्षैतिज से 60° के कोण पर एक 9 kg के पिंड पर आरोपित है । पिंड में क्षैतिज दिशा में कितना त्वरण है ? ( 4 m/s²)

(4) 3kg के पिंड पर आरोपित नियत बल 25 sec में पिंड का वेग 2 m/s से बढ़कर 3.5 m/s कर देता है । बल का परिमाण तथा दिशा ज्ञात करें ।( 0.18N)

(5) एक बन्दुक द्वारा 200 ग्राम की एक गोली 20 m/s के वेग से लकड़ी के बक्से की तरफ दागी जाती है । गोली बक्से में 40 सेमी धसने के पश्चात् रुक जाती है । बक्से द्वारा गोली पर लगाया गया बल मंदन बल ज्ञात करें । ( 100 न्यूटन )

(6) 10 kg द्रव्यमान की एक वस्तु पर 6 N तथा 8 N के बल परस्पर लंबवत दिशा में लग रहे है । तो ज्ञात करो (a) वस्तु का परिणामी बल (b) त्वरण का परिमाण तथा दिशा (10 N , 1 m/s², 37°)

(7) 20 kg द्रव्यमान की वस्तु 5 m/s के वेग से गति करता है । यदि वस्तु पर 40 N का मंदन बल लगाया जाये तो कितने समय के बाद वस्तु रुक जाएगी । (2.5 sec)

(8) 12 m/s के वेग से गतिमान 0.25 kg की एक वस्तु को 0.6 N का बल लगाकर रोका जाता है । वस्तु कितने समय में रुक जाएगी ? बल का आवेग भी ज्ञात करें । (5 sec , 3.0 N-s)

(9) 10 N का एक बल दो द्रव्यमान m तथा M में क्रमशः 10 m/s² तथा 20 m/s² का त्वरण उत्पन्न करता है । यदि दोनों कणों को जोड़ दिया जाये तो परिणामी त्वरण ज्ञात करें । (6.66 m/s²)

(10) 0.2kg द्रव्यमान की क्रिकेट गेंद 20 m/s के वेग से गतिमान है । जिसे 0.4 sec में विराम अवस्था में लाया जाता है । औसत बल ज्ञात कीजिये । (10 N)

(11) \fn_cm 3\times10^7 \;kg द्रव्यमान का जहाज जो की प्रारंभिक अवस्था में विराम में है । \fn_cm 5\times10^4 N का बल लगाकर 3 मीटर दुरी तक खिंचा जाता है । जल का प्रतिरोध नगण्य है तो जहाज की चाल ज्ञात करें । (0.1 m/s)

(12) एक लड़का 15 Kg की गाड़ी को एक रस्सी के द्वारा घर्षण रहित सड़क पर खींचता है । वह रस्सी पर क्षैतिज से 30° ऊपर की ओर बल लगाता है । गाड़ी को 3 m/s² के त्वरण से चलाने के लिए कितना बल लगाना होगा . ( 52 N)

(13) एक मशीन गन 40 ग्राम की एक गोली 1200 m/s के वेग से छोड़ती है । यदि मशीन गन चलाने वाला व्यक्ति प्रति सेकंड 3 गोलियां छोड़ रहा हो , तो उसे मशीन गन पर कितना बल लगाना होगा ? (144N)

प्रकृति के 4 मूल बल

1. गुरुत्वाकर्षण बल :-

प्रत्येक पिंड दूसरे पिंड पर द्रव्यमान के कारण आकर्षण बल लगाता है ,जिसे गुरुत्वाकर्षण बल कहते है।

2. विधुत चुम्बकीय बल :-

” दो आवेशित कणो के मध्य लगने वाला बल विधुत चुम्बकीय बल कहलाता है।” संपर्क बल , घर्षण बल , अभिलम्ब प्रतिक्रिया बल , तनाव बल , स्प्रिंग बल इत्यादि सभी विधुत चुम्बकीय बल के उदहारण है।

(a) संपर्क बल:-

जब दो वस्तुएं आपस में संपर्क में आती है तो उनके बीच संपर्क बल लगता है। संपर्क – पृष्ठों के अभिलम्ब संपर्क बल के घटक को अभिलम्ब प्रतिक्रिया बल (N) कहते है। तथा संपर्क पृष्ठों के समान्तर घटक को घर्षण बल (f) कहते है।

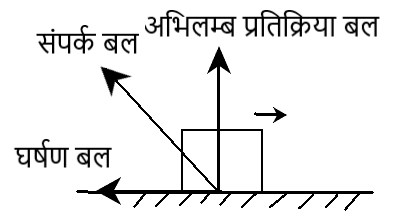
नोट:- संपर्क बल तब भी उत्पन्न होते है , जब ठोस तरलों के संपर्क में आते है।

(b) तनाव बल :-

( जब डोरी में तनाव हो तो प्रत्येक भाग में तनाव बल (T)  लगता है )

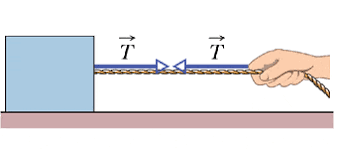
(नगण्य द्रव्यमान की डोरी के लिए डोरी के प्रत्येक भाग पर समान तनाव माना जा सकता है। )

(c) स्प्रिंग बल :-

जब हम किसी स्प्रिंग को दबाते या खींचते है तो स्प्रिंग अपनी मूल अवस्था में आने के लिए बल लगाता है जिसे स्प्रिंग बल कहते है। यह बल स्प्रिंग में उत्पन्न विस्थापन के समानुपाती होती है। \dpi{120} \fn_cm \left (F\propto x \;\;\;\;\; or \;\;\;\;F=-kx \right )

जहाँ \dpi{120} \fn_cm k एक नियतांक है , जिसे स्प्रिंग नियतांक कहते है ।

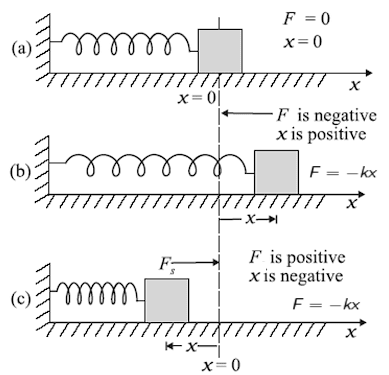
NOTE:- स्प्रिंग बल को आगे के अध्याय ” कार्य ऊर्जा तथा शक्ति ” में विस्तार पूर्वक बताया गया है ।

3. प्रबल नाभिकीय बल :-

नाभिक में प्रबल नाभिकीय बल के कारण न्यूट्रॉन तथा प्रोटॉन एक दूसरे से बंधे रहते है। यह बल सभी बलों में सबसे प्रबलतम होता है। यह आवेश के प्रकार पर निर्भर नहीं करता है।

4. दुर्बल नाभिकीय बल :-

नाभिक में बीटा क्षय के दौरान यह एक इलेक्ट्रान तथा एक अनावेशित कण के मध्य पाया जाने वाला एक आकर्षण बल है। यह अत्यंत दुर्बल होता है। अनावेशित कण के रूप में न्युट्रीनो नाभिक में पाया जाता है |

 

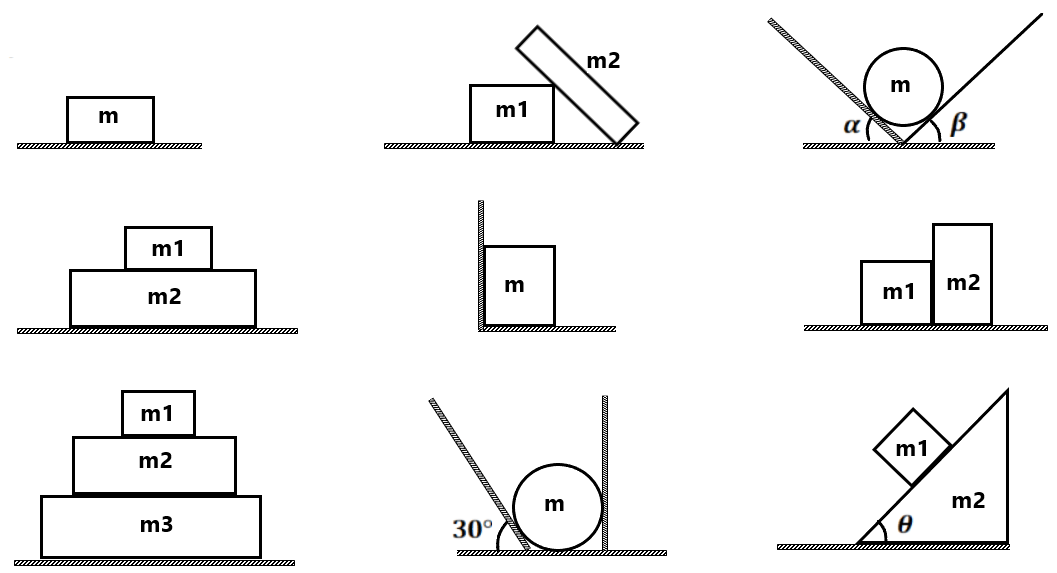
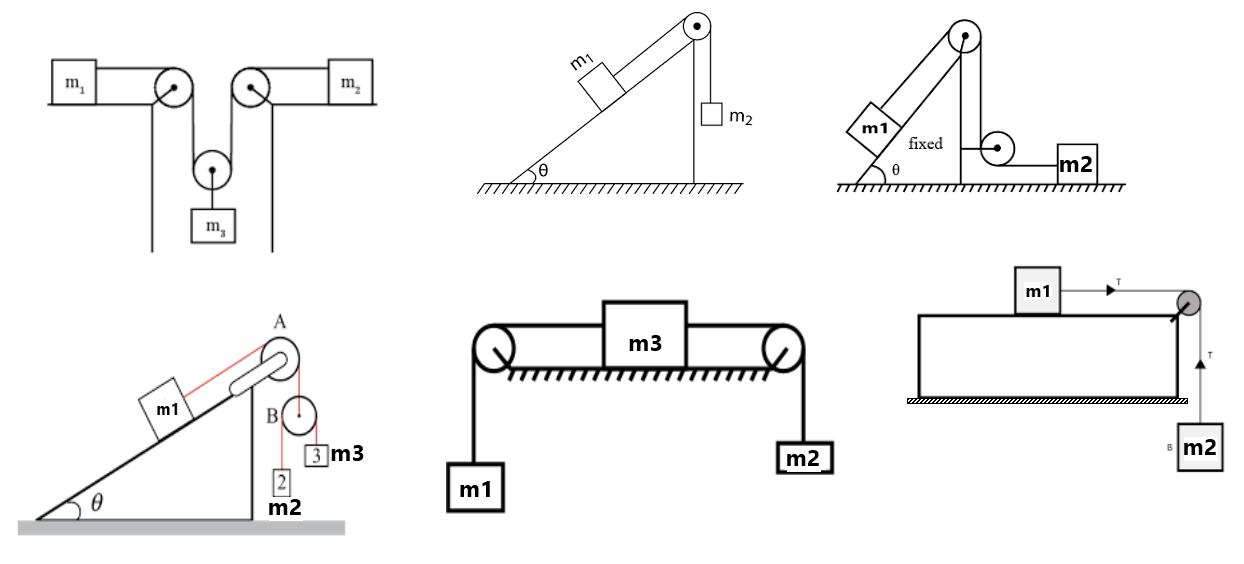
प्रत्येक वस्तु में FBD (Free Body Diagram) को  दर्शाएं

 

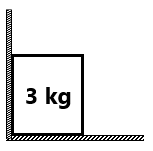
संख्यात्मक प्रश्न 

(1) अभिलम्ब प्रतिक्रिया बल ज्ञात करे  (a) वस्तु तथा फर्श के बीच  (b) वस्तु तथा दीवार के बीच ( 30N, 0)

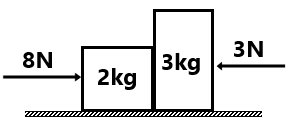
(2) 2kg तथा 3kg द्रव्यमान के बीच अभिलम्ब प्रतिक्रिया बल ज्ञात करें . (6N)

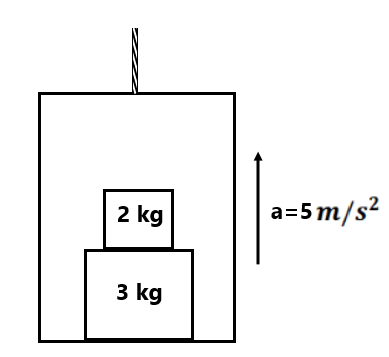
(3) अभिलम्ब  प्रतिक्रिया बल ज्ञात करें (a) 2kg तथा  3 kg वस्तु के बीच (b) 3kg तथा लिफ्ट के बीच

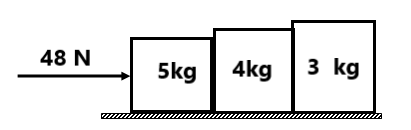
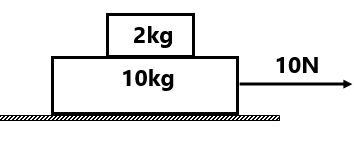
(4) वस्तुओं के बीच अभिलम्ब प्रतिक्रिया बल निकले तथा त्वरण ज्ञात करें . (4 m/s², 12N, 28N)

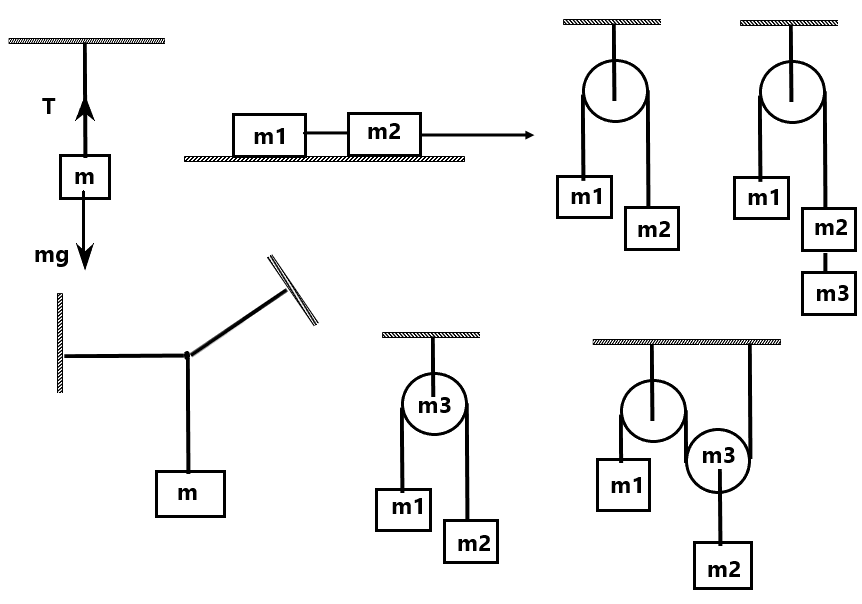
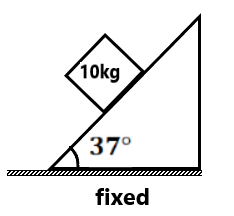
(5) 10kg द्रव्यमान का त्वरण ज्ञात करें ।

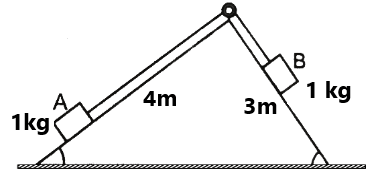
(6) चित्र में दोनों वस्तुओं का त्वरण ज्ञात करें . ( 1m/s², 0)

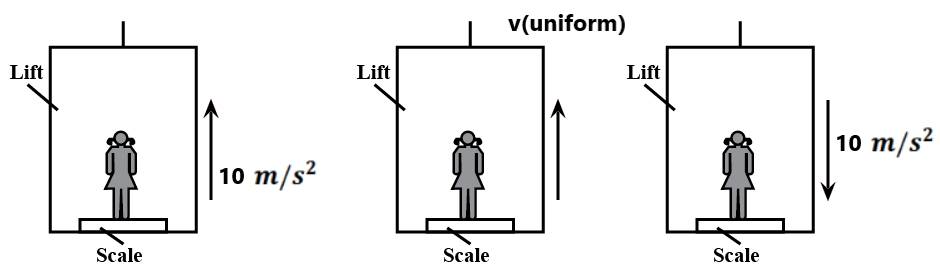
(7) 60kg व्यक्ति का भार मापी पैमाने पर पाठ्यांक क्या होगा ?

(8) किसी 60kg व्यक्ति का निम्न स्थितियों में भार मापी पैमाने पर पाठ्यांक क्या होगा ?

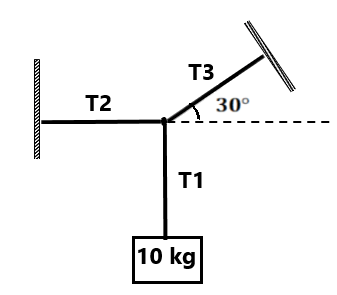
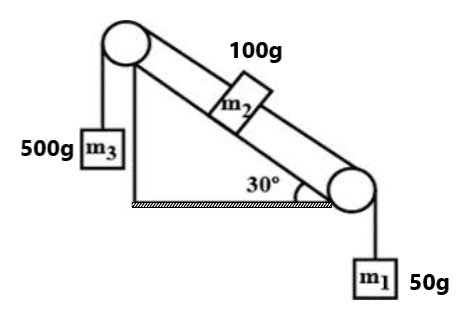
(9) दिए गए चित्र में 10 kg वस्ति सम्य्वस्था में है .  T1, T2 तथा  T3 का मान ज्ञात करें . (100N, 100√3 N, 200N)

(10) गोले में लगने वाले सभी अभिलम्ब प्रतिक्रिया बल का मान ज्ञात करें . ( 50N, 50√3 N)

(11) A , B तथा C पर तनाव बल ज्ञात करे . यदि रस्सी 1 kg का हो तथा उसका द्रव्यमान समरूप वितरण में हो . (10N, 9N, 8N)

(12) T2 का मान ज्ञात करे . (30N)

(13) वस्तु का त्वरण ज्ञात करें . (2.5 m/s²)

(14) वस्तु का त्वरण तथा रस्सी में तनाव ज्ञात करें . (4 m/s², 60N, 84N)

(15) वस्तु का त्वरण तथा रस्सी में तनाव ज्ञात करें . (4 m/s², 90N)

(16) 5kg का बन्दर एक रस्सी में चढ़ रहा है जिसका अधिकतम तनाव 150N है , अंदर का महत्तम त्वरण ज्ञात करें जब बन्दर  (g=9.8m/s²) (20 m/s²,10 m/s²)

(a) ऊपर की ओर चढ़ रहा है
(b) निचे उतर रहा हो

(17) रस्सी के P बिंदु पर तनाव का मान ज्ञात करें  . (164N)

(18) वस्तु को ज़मीन से ऊपर जाने के लिए बन्दर को रस्सी में चढ़ना होगा  (correct option a)

(a) समरूप त्वरण  5m/s² से अधिक
(b) समरूप त्वरण  2.5 m/s² से अधिक .
(c) समरूप गति से

(19) बन्दर A अपनी पूंछ पर 30N का तनाव झेल सकता है , वह रस्सी पर कितना बल लगाए ताकि बन्दर B को अपने साथ ऊपर की ओर ले जा सके ।? (g=10m/s²) (between 70N to 105N)

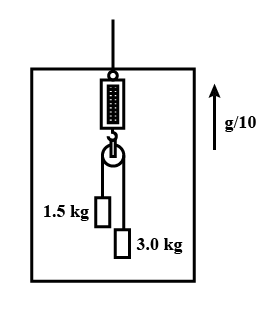
(20) दोनों स्थिति में वस्तु में उत्पन्न त्वरण का मान निकले  (8g/13 m/s², g/10 m/s²)

             

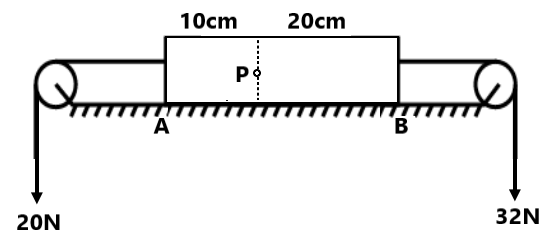
(21) P पर बल का मान निकले जबकि रॉड का द्रव्यमान =3 kg ( समरूप वितरित द्रव्यमान  ) (24N)

(22) M द्रव्यमान युक्त गुब्बारा a त्वरण से निचे उतर रहा है जहाँ a<g , इसके अंशों का कितना द्रव्यमान हटा देना चाहिए ताकि यह ‘a’ त्वरण से ऊपर गति करना आरम्भ कर गए ? \fn_cm \left ( \frac{2Ma}{g+a}\right )

(23) पैमाने पर पाठ्यांक निकाले । (4.4 kg)

(24) रस्सी में उत्पन्न तनाव का मान ज्ञात करें यदि लिफ्ट

(a) ऊपर की ओर  1.2 m/s² त्वरण से जा रही हो . (0.55 N)
(b) ऊपर की ओर  1.2 m/s² मंदन से जा रही हो .(0.43N)
(c) ऊपर की ओर समरूप गति से जा रही हो .(0.49 N)
(d) निचे की ओर  1.2 m/s² त्वरण से जा रही हो. (0.43N)
(e) निचे की ओर  1.2 m/s² मंदन से जा रही हो .( 0.55 N)
(f) निचे की ओर समरूप गति से जा रही हो. (0.49 N)

(25) दिए गए चित्र में भार मापी पैमाने पर पाठ्यांक क्या होगा. (mcosθ)

 

रेखीय संवेग संरक्षण का सिद्धांत

हम जानते है की किसी निकाय के लिए \dpi{120} \fn_cm \vec{F}_{ext}=\frac{d\vec{p}}{dt}

यदि उस निकाय में कुल वाह्य बल शून्य हो तो \dpi{120} \fn_cm \vec{F}_{ext}=0

अर्थात \dpi{120} \fn_cm \frac{d\vec{p}}{dt}=0

अतः \dpi{120} \fn_cm \vec{p}= नियतांक , यही संवेग संरक्षण का सिद्धांत है ।

अतः हम कह सकते है की ” वाह्य बल की अनुपस्थिति में किसी निकाय का कुल संवेग नियत रहता है ।”

अर्थात निकाय का अंतिम संवेग = निकाय का प्रारंभिक संवेग

संवेग संरक्षण के नियम के व्यावहारिक उपयोग

  1. जब बन्दुक से गोली चलाई जाती है, तो बन्दुक पीछे की ओर धक्का लगाती है ।
  2. रॉकेट की गति संवेग संरक्षण के सिद्धांत पर ही आधारित है ।
  3. बम के फटने के बाद बम के कणो का छितरा जाना ।
  4. यदि अंतरिक्ष में कोई यात्री अपने यान से दूर है और वह यान पर वापस लौटना चाहता है तो उसे यान की गति के विपरीत दिशा में कोई वस्तु फेंकनी चाहिए ।

रॉकेट नोदन ( परिवर्ती द्रव्यमान का उदाहरण )

कृत्रिम उपग्रहों को पृथ्वी की सतह से निश्चित ऊंचाई पर उनकी कक्षा में ले जाने के लिए राकेट की आवश्यकता होती है । रॉकर प्रक्षेपण या नोदन संवेग संरक्षण के सिद्धांत पर आधारित है । राकेट नोदन में ईंधन के दहन से गैसें बहार निष्कासित होती है , जिससे पीछे की ओर संवेग उत्पन्न हो जाता है जो राकेट को आगे की ओर गति प्रदान करता है ।

यदि गैसों के निष्कासन की दर निश्चित हो तो संवेग परिवर्तन की दर भी निश्चित होगी । किन्तु गैसों के निष्कासन के कारण राकेट का द्रव्यमान निरंतर घटता जाता है । इसीलिए त्वरण निश्चित नहीं रहता है । फलस्वरूप राकेट का वेग तथा त्वरण बढ़ते जाते है ।

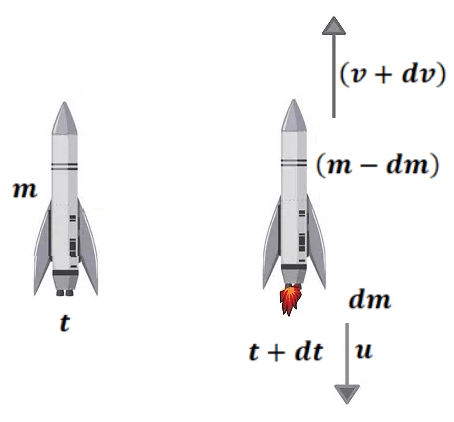
माना की बाह्य अंतरिक्ष में एक राकेट गतिशील है जहाँ पर कोई भी बाह्य बल नहीं लग रहा है ।

माना किसी क्षण t=t में राकेट का द्रव्यमान \dpi{120} \fn_cm m तथा वेग \fn_cm v है । \fn_cm dt समय के बाद \fn_cm dm द्रव्यमान का गैस \fn_cm u वेग के साथ ( पृथ्वी के सापेक्ष ) रॉकेट से निकलती है जैसा की चित्र में दिखाया गया है ।

\fn_cm \because  निकाय का कुल संवेग अचर है, अर्थात \fn_cm dt समय के बाद रॉकेट का द्रव्यमान \fn_cm (m-dm) तथा वेग \fn_cm (v+dv) हो जाता है ।

यहाँ पर गैस का वेग रॉकेट के सापेक्ष अचर है जिसे \fn_cm v_{rel} से सूचित किया जाता है ।

आपेक्षिक वेग के अनुसार \dpi{120} \fn_cm v_{rel}=u+v+dv\;\;\;\;\;\therefore \;u=v_{rel}-v-dv---(1)

संवेग संरक्षण के अनुसार

प्रारंभिक संवेग = अंतिम संवेग

\dpi{120} \fn_cm \Rightarrow mv=(m-dm)(v+dv)-dm\;u

समीकरण (1) से

\dpi{120} \fn_cm \Rightarrow mv=mv+mdv-dm\;v-dmdv-dm(v_{rel}-v-dv)

\dpi{120} \fn_cm \Rightarrow mv=mv+mdv-dm\;v-dmdv-dmv_{rel}+dm\;v+dmdv

\dpi{120} \fn_cm \left [ mdv=v_{rel}dm \right ]-----(a)

दोनों तरफ \fn_cm dt से भाग देने पर

\dpi{120} \fn_cm m\frac{dv}{dt}=v_{rel}\frac{dm}{dt}

समीकरण में बायाँ तरफ गैस के द्वारा रॉकेट पर लगाया गया क्षणिक बल है , जिसे रॉकेट पर लगा किसी क्षण का प्रणोद (Thrust) कहते है । अर्थात

\dpi{150} \fn_cm \left [ F_r=v_{rel}\frac{dm}{dt} \right ]

किसी भी क्षण राकेट का वेग 

चूँकि राकेट का ईंधन जलने के कारण जैसे जैसे राकेट का कुल द्रव्यमान घटता जाता है , उसका वेग बढ़ता जाता है । अतः समीकरण (a) को निम्न रूप से लिख सकते है ।

\dpi{120} \fn_cm mdv=-v_{rel}dm

\dpi{120} \fn_cm dv=-v_{rel}\frac{dm}{m}

दोनों तरफ integration करने पर

\dpi{120} \fn_cm \int_{v_0}^{v}dv=-v_{rel}\int_{m_0}^{m}\frac{dm}{m}

\dpi{120} \fn_cm \left [ v \right ]_{v_0}^{v}=-v_{rel}\left [ log\;m \right ]_{m_0}^{m}

\dpi{120} \fn_cm v-v_0=v_{rel}\left [ log \;m_0-log\;m \right ]

\dpi{120} \fn_cm v-v_0=v_{rel}\log_{e}\frac{m_0}{m}

\dpi{150} \fn_cm \left [ v=v_0+v_{rel}\log_{e}\frac{m_0}{m} \right ]

यदि रॉकेट का प्रारंभिक शून्य हो तो , \fn_cm \large v_0=0

अर्थात \dpi{150} \fn_cm \left [ v=v_{rel}\log_{e}\frac{m_0}{m} \right ]

 

संख्यात्मक प्रश्न 

(1) 10 kg द्रव्यमान की रायफल से 0.02 gram द्रव्यमान की गोली 1000 m/s की चाल से निकलती है । राइफल किस चाल से पीछे लौटेगी । (2 m/s)

(2) 500 gram द्रव्यमान की एक ट्राली 70 cm/s के वेग से चल रही है । चलती हुई ट्राली पर धीरे से 200 gram द्रव्यमान का एक पिंड रख देने से ट्राली का वेग कितना हो जायेगा । (50 cm/sec)

(3) 5 kg का स्थिर बम अचानक दो टुकड़ो में फटता है । 4 kg का एक टुकड़ा 50 m/s के वेग से बायीं ओर जाता है । 1 kg के टुकड़े की गति बतलाइये । (200 m/s दायीं ओर )

(4) 40 Kg और 20 Kg द्रव्यमान के दो गोलाकार पिंड 10 m/s एवं 50 m/s के वेग से चल रहे है । इनकी दिशा एक दूसरे की ओर है । कुछ समय पश्चात् टकराने पर वे जुड़कर एक निकाय बनाते है । निकाय का वेग ज्ञात कीजिये । (10 m/s)

(5) 10 kg का एक पिंड 20 m/s की चाल से दायीं ओर जाते हुए विपरीत दिशा में समान चाल से गतिमान एक पिंड से जिसका द्रव्यमान 6 kg है, टकरा जाता है । टक्कर के पश्चात् संयुक्त पिंड का वेग क्या होगा ? (5 m/s दायीं ओर )

(6) 100 kg का एक तोप से 0.02 kg द्रव्यमान का एक गोला 80 m/s के वेग से दागा जाता है । तोप का प्रतिक्षिप्त वेग (recoil velocity) क्या होगा ? ( 0.016 m/s)

(7) 200 m/s की चाल से चलती हुई एक गोली बालू की थैली में धंसकर उसी में रह जाती है । गोली एवं थैली का द्रव्यमान क्रमशः 0.5 kg तथा 4.5 kg है । यदि थैली गति के लिए स्वतंत्र हो तो उसकी चाल कितनी होगी । (20 m/s)

(8) 5 kg  द्रव्यमान का एक गतिशील पिंड A किसी अन्य स्थिर पिंड B से टकराता है । यदि टक्कर के पश्चात् दोनों पिंड उसी दिशा में पिंड A की एक तिहाई चाल से गतिशील हो जाये , तो पिंड B का द्रव्यमान ज्ञात कीजिये । (10 kg)

(9) एक शिकारी अपनी मशीन गन से 50 ग्राम द्रव्यमान वाली गोलियां 150 m/s के वेग से चलाती है । 60 kg द्रव्यमान का चीता उसकी ओर 10 m/s के वेग से झपट्टा मरता है । शिकारी को चीते में कितनी गोलियां मारनी चाहिए की वह बीच रस्ते में ही गिर पड़े ? (80 गोलियां )

(10) 1000 kg द्रव्यमान की एक कार 32 m/s के वेग से आती हुई , 4 m/s के वेग से उसी दिशा में जाते हुए , 8000 kg के ट्रक के पीछे से टकराती है । टक्कर के बाद उलटी दिशा में 8 m/s के वेग से लौटती है । टक्कर के पश्चात् ट्रक का वेग कितना है ? ( 9 m/s उसी दिशा में )

(11) 10 kg का एक बम तीन टुकड़ो में फटता है । दो टुकड़े जिनके द्रव्यमान 3kg एवं 2kg है क्रमशः 8m/s तथा 12 m/s के वेगों से परस्पर विपरीत दिशाओं  में जाते है । तीसरे टुकड़े का वेग क्या होगा । ( शून्य )

(12) कोई शिकारी 5 kg की बन्दुक से 10 gram की गोली 400 m/s के वेग से छोड़ता है । बन्दुक का प्रतिक्षिप्त वेग ज्ञात कीजिये । यदि शिकारी बर्फ पर खड़ा हो तब वह ( बन्दुक सहित ) कितना वेग प्राप्त करेगा ? शिकारी का द्रव्यमान 75 kg है । (0.8 m/s, -0.05 m/s)

(13) एक राकेट का द्रव्यमान \fn_cm 1.3\times10^4 \;kg का है । इसका इंजन इस पर ऊपर की ओर \fn_cm 2.6\times10^5\;N का प्रारंभिक प्रणोद (Thrust) लगाता है । राकेट को कितना प्रारंभिक त्वरण मिलेगा ? (10.2 m/s²)

(14) एक राकेट 50 gram/sec की दर से ईंधन जला रहा है तथा इसे \fn_cm 5\times10^3 m/s के सापेक्ष वेग से गैस – जेट के रूप में बाहर फेंकता है । यह गैस राकेट पर कितना प्रतिक्रिया बल लगा रही है । ( 250 N)

(15) एक रॉकेट का द्रव्यमान 500 kg है तथा उससे निकलने वाली गैसों का रॉकेट के सापेक्ष वेग 250 m/s है । ज्ञात कीजिये की रॉकेट को ऊपर की ओर ऊर्ध्वाधर दिशा में 20 m/s² का त्वरण प्रदान करने के लिए ईंधन किस दर से जलाना होगा । (g=10 m/s²) ( 60 kg/sec)

(16) एक गेंद जिसकी चाल 9 m/s है , ठीक ऐसी ही एक दूसरी स्थिर गेंद से टकराती है । टक्कर के पश्चात् दोनों गेंदें मूल गति की दिशा से 30° कोण बनती हुई गति करती है जैसा की चित्र में दिखाया गया है । टक्कर के पश्चात् गेंदों की चाल कितनी है ? ( 5.2 m/s)

 

आवेग :-

जब किसी वस्तु पर बहुत कम समय के लिए बहुत ही ज्यादा बल लगाया जाता है तो इस बल को आवेगी बल कहते है। उदहारण के लिए हथौड़े से कील ठोंकना , बल्ले से गेंद को मारना | इस क्रम में सामान्यतः बल नियत नहीं रहता है , बल्कि समय के साथ परिवर्तनशील रहता है।
इसमें औसत बल तथा समय का गुणनफल ( जिसे आवेग कहते है ) एक योग्य राशि है जो वास्तव में पिंड का संवेग परिवर्तन है।

“अतः किसी वस्तु पर बहुत कम समय तक लगने वाले बल के कुल प्रभाव को बल का आवेग कहते है और इसकी माप औसत बल तथा समय के गुणनफल से कि जाती है। ” इसे J द्वारा सूचित किया जाता है

अर्थात                    आवेग  \dpi{120} \fn_cm \vec{J}=\vec{F}_{avg}\times\Delta t

यह एक सदिश राशि है तथा इसकी दिशा बल की दिशा कि ओर होती है। इसका S.I मात्रक N-s होता है ।

न्यूटन के गति के द्वितीय नियम के अनुसार \dpi{120} \fn_cm \vec{F}=\frac{d\vec{p}}{dt}

\dpi{120} \fn_cm \Rightarrow \vec{F}dt=d\vec{p}

\dpi{120} \fn_cm \Rightarrow \int_{t_1}^{t_2}\vec{F}dt=\int_{\vec{p}_1}^{\vec{p}_2}d\vec{p}

\dpi{120} \fn_cm \Rightarrow \;\;\;\left [\vec{J}= \vec{p}_2 -\vec{p}_1 \right ]

इस प्रकार संवेग में परिवर्तन आवेग के बराबर है । ( इसे आवेग संवेग प्रमेय कहते है )

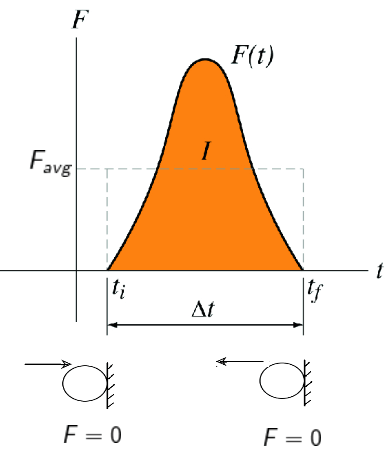
NOTE:- \dpi{120} \fn_cm F_{avg} तथा \dpi{120} \fn_cm t ( समय ) ग्राफ में समय अक्ष के बीच घिरा क्षेत्रफल आवेग के संख्यात्मक मान को बतलाती है जो संवेग परिवर्तन के बराबर होती है ।

उदाहरण :-

  1. एक क्रिकेट खिलाडी अपने हाथों को पीछे की ओर ले जाता है , जब वह गेंद को पकड़ता है ।
  2. सीमेंट युक्त फर्श पर गिरने वाला व्यक्ति को बालू के ढेर पर गिरने वाले व्यक्ति की अपेक्षा अधिक चोट लगती है ।
  3. वाहनों में स्प्रिंग ( शॉकर ) लगाए जाते है ।
  4. कांच के बने पदार्थ और चीनी मिटटी के बने बर्तन धुलाई से पहले घास के टुकड़ो में लपेटा जाता है ।
  5. रेलगाड़ी के डब्बों में बम्फर लगाए जाते है ।
  6. क्रिकेट की गेंद की अपेक्षा टेनिस के गेंद पकड़ना अधिक आसान है ।
  7. दुर्घटना में व्यक्ति की हड्डियां टूट जाती है ।

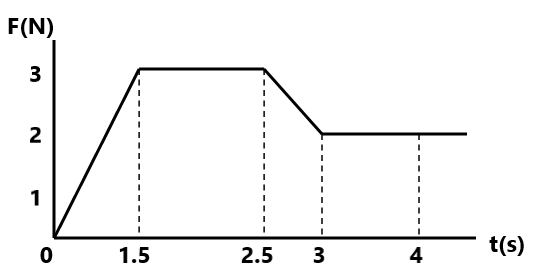
संख्यात्मक प्रश्न 

(1) 10 ग्राम द्रव्यमान की कांच की गोली 40 मीटर ऊंचाई से गिरती है और पुनः 10 मीटर की ऊंचाई तक उछलती है । कांच की गेंद द्वारा फर्श पर आरोपित आवेग की मात्रा तथा औसत बल की गणना कीजिये । ( 0.42 N-s, 4.2 N)

(2) 100 ग्राम द्रव्यमान की गेंद 10 m/s के वेग से गतिमान है, एक लड़का प्रतिरोधी बल लगाकर 0.02 सेकंड में उसे विरामावस्था में ले आता है तो ज्ञात कीजिये । (a) गेंद का आवेग (b) लड़के द्वारा आरोपित बल ( 1 N-s, 50N)

(3) 50 ग्राम द्रव्यमान की गेंद 500 m/s के वेग से गतिशील है , प्रतिरोध बल लगाकर 0.01 सेकंड में विरामावस्था में ले जाती है । आवेग तथा आरोपित बल ज्ञात कीजिये । ( -25 N-s, -2500 N)

(4) एक बल्लेबाज प्रारंभिक चाल परिवर्तित किये बिना गेंद को 45° कोण से विक्षेपित कर देता है , उसकी प्रारंभिक चाल 54 km/h के बराबर है । गेंद को प्रदान किया गया आवेग क्या होगा ? गेंद का द्रव्यमान 0.15 kg है । (4.16 kgm/s)

(5) 60 kg द्रव्यमान की एक गेंद को स्ट्राइकर द्वारा मारा जाता है । गेंद एक समान मंदन 4 m/s² से गति करते हुए 50 मीटर की क्षैतिज दुरी तय करके रुक जाती है तो गेंद पर लगे शॉट का आवेग ज्ञात करें । (1.2 N.s)

(6) 0.1 kg द्रव्यमान की गेंद की दीवार की ओर फेंका जाता है । यह गेंद 30 m/s के वेग से दीवार पर टकराती है और पुनः 20 m/s के वेग से वापिस आती है । गेंद द्वारा दीवार पर लगाए गए बल का आवेग ज्ञात कीजिये । (5 N-s)

(7) एक वस्तु का द्रव्यमान 2 kg है तथा प्रारंभिक वेग 5 m/s है । वस्तु की गति की दिशा में एक बल 4 सेकंड के लिए कार्य करता है । बल समय ग्राफ चित्र के अनुसार है । वस्तु का आवेग तथा वेग की गणना करें । ( 8.5 N , 9.25 m/s)

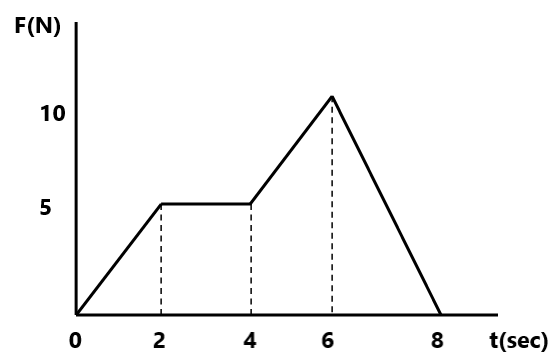
(8)  10 kg द्रव्यमान का एक पिंड 8 m/s के वेग से जा रहा है । इस पर आरोपित बल का परिमाण चित्र में दिखाए गए अनुसार बदल रहा है ।

ज्ञात कीजिये की

(a) पिंड का प्रारंभिक वेग क्या है ?
(b) t=3 सेकंड पर पिंड का संवेग क्या है ?
(c) बल की अधिकतम स्थिति में पिंड का संवेग क्या है ?
(d) बल शून्य होने की स्थिति में पिंड का संवेग क्या है ?  (10 kgm/s, 90 kgm/s, 110 kgm/s, 120 kgm/s)

 

प्रश्न

(1) बल का आवेग पिंड के _________ में परिवर्तन के बराबर होता है ।

(2) किसी पिंड में उसकी गति की कुल मात्रा को ________ कहते है ।

(3) न्यूटन के गति के ________ नियम से जड़त्व की परिभाषा प्राप्त होता है ।

(4) बल का C.G.S मात्रक ________ तथा गरुत्वीय मात्रक ________ है ।

(5) ________ की अनुपस्थिति में कणों के किसी निकाय का कुल संवेग नियत रहता है ।

(6) न्यूटन के गति के ________ नियम ही गति का वास्तविक नियम है ।

(7) बल और समय अंतराल ( जब तक की बल लगता है ) के गुणनफल को ________ कहते है ।

(8) राकेट नोदन ________ के नियम पर आधारित है ।

(9) क्रिया और प्रतिक्रिया बल ______ वस्तु पर कार्य नहीं करते है ।

(10) किसी क्षैतिज घर्षण रहित समतल पर रखी 2 kg और 3 kg द्रव्यमान की दो वस्तुएँ एक भारहीन धागे से बंधी है । यदि 3 kg की वस्तु पर 30N का बल लग रहा हो तो 2 kg द्रव्यमान पर ________ N का बल लगेगा। ( 12N)

(11) प्रकृति का सर्वाधिक प्रबल बल __________ तथा सर्वाधिक निर्बल बल __________ होता है ।

(12) दौड़ता हुआ व्यक्ति ठोकर लगने पर आगे की ओर गिरता है , यह _________ का उदहारण है ।

(13) पृथ्वी जितने बल से किसी पिंड को अपनी ओर आकर्षित करती है , वह उस वस्तु का ________ कहलाता है ।

(1) जब बस अचानक रूकती है तो , यात्री आगे की ओर क्यों गिरती है ?

(2) क्रिकेट खिलाडी गेंद पकड़ते समय हाथों को पीछे क्यों ले जाता है ?

(3) जब एक बस विराम से अचानक चले तो यात्री पीछे की ओर धक्का अनुभव क्यों करते है ?

(4) यदि एक जैसी गोलियों को हलकी व भारी राइफल से समान वेग से छोड़ा जाये तो हलकी राइफल भारी राइफल की अपेक्षा बड़ा झटका देती है । क्या कारण है ?

(5) एक धावक कूदने से पहले कुछ दूर क्यों दौड़ता है ?

(6) दीवार में कील अधिक गहराई तक गाड़ने के लिए भारी हथौड़े अधिक उपयुक्त होता है, क्यों ?

(7) विधुत आपूर्ति बंद करने के बाद भी पंखा कुछ समय तक घूमता रहता है , क्यों ?

(8) चलती बस से सुरक्षित उतरने के लिए बस की दिशा में कुछ दूर दौड़ना पड़ता है । क्यों ?

(9) क्रिया तथा प्रतिक्रिया बल समान एवं विपरीत है । फिर भी ये एक दूसरे को संतुलित नहीं करते है , क्यों ?

(10) एक बन्दुक से गोली दागने पर बन्दुक पीछे की ओर प्रक्षेपित होती है, क्यों ?

(11) जब कोई गेंद ऊपर की और फेंकी जाती है तो उसका संवेग पहले घटता है , फिर बढ़ता है , क्या इस प्रक्रिया में संवेग – संरक्षण का उलंघन होता है ।

(12) पेड़ की शाखा की हिलने पाए आम निचे क्यों गिरता है ?

(13) रेल के डिब्बों के मध्य बम्फर क्यों लगाते है ?

(14) एक वैज्ञानिक अंतरिक्ष में अपने यान से दूर है । वह कैसे अपने यान पर लौट का आ सकता है ।

(15) एक व्यक्ति सीमेंट के फर्श पर गिरता है तो रेत की ढेरी पर गिरने की बजाये ज्यादा चोट लगती है, क्यों ?

(16) समान वेग से गतिशील क्रिकेट की बॉल को टेनिस की बॉल की चलता में पकड़ना कठिन है , क्यों ?

(17) कोई वस्तु को साम्यावस्था में होने के लिए क्या शर्त है ।

(18) एक वस्तु पर कई बाह्य बल लगते है , क्या वह वस्तु साम्यावस्था में रह सकती है ?

(19) जब कोई वस्तु पृथ्वी की ओर गिरती है , तो पृथ्वी भी ऊपर की ओर गति करती है । परन्तु पृथ्वी की गति को देखा नहीं जा सकता है , क्यों ?

(20) 10 ग्राम की वस्तु निर्वात में नियत वेग 10 m/s से क्षैतिज घर्षण रहित तल पर गति करती है । वस्तु पर बल क्या होगा ?

(21) यदि एक डोरी के सिरे पर एक पत्थर को तेजी से घुमाया जाता है तभी यह टूट जाती है तथा पत्थर स्पर्श रेखीय रूप से दूर चला जाता है । समझाइये क्यों ?

(22) जब एक व्यक्ति नाव के बाहर कूदता है तो नाव में थोड़ी दूर तक धक्का लगता है । क्यों ?

(23) दो लड़के बर्फ स्केट पर अपने बीच एक रस्सी पकडे खड़े है । एक लड़का दूसरे से अधिक भारी है । हलके भार वाला लड़का रस्सी खींचता है । उसकी गति को समझाइये ।

(24) हम ऊपर की चढ़ने के लिए रस्सी को निचे की ओर क्यों खींचते है ?

(25) न्यूटन कि गति का कौन स नियम रॉकेट की गति में लागू होता है ?

 

प्रश्न 

(1) जड़त्व से आप क्या समझते है ? जड़त्व के तीनो प्रकारों को समझाइये ।

(2) एक विलगित निकाय से आप क्या समझते है ?

(3) रेखीय संवेग के संरक्षण के सिद्धांत को समझाइये ।

(4) न्यूटन के गति के सभी नियमों को लिखे ।

(5) बल का गरूत्व इकाई क्या है ?

(6) आवेग किसे कहते है , यह संवेग परिवर्तन के बराबर है , कैसे ?

(7) सिद्ध कीजिये कि न्यूटन के गति का द्वितीय नियम ही गति का वास्तविक नियम है ।

(8) न्यूटन के द्वितीय नियम से F=ma को सत्यापित करें ।

(9) संवेग संरक्षण नियम लिखिए तथा इसकी सहायता से गति के तृतीय नियम को निगमित कीजिये ।

(10) राकेट नोदन के सिद्धांत की व्याख्या कीजिये तथा राकेट पर लगने वाले प्रणोद के लिए सूत्र स्थापित कीजिये

  विद्यार्थी NCERT के प्रश्न को भी हल करें 

error: