समतलीय गति
जब कोई वस्तु एक समतल में गति करता है , तो उसकी गति को समतलीय गति अथवा द्विविमीय गति कहते है ।
द्विविमीय गति = एक विमीय गति + एक विमीय गति
अर्थात किसी समतल ( दो विमीय ) में गति को दो अलग अलग – अलग समकालिक एक विमीय गति गतियों के रूप में समझ सकते है , जो परस्पर लंबवत दिशाओं के अनुदिश हो ।
अतः एक विमीय गति का सूत्र हम द्विविमीय गति में उपस्थित दो समकालिक एक विमीय गति में स्वतंत्र रूप से लगा सकते है ।
द्विविमीय गति के लिए
उसी प्रकार
संख्यात्मक प्रश्न ( Numerical)(1) एक कण x-y तल के मूल बिंदु से चलना आरम्भ करता है और 2 sec के पश्चात बिंदु (3,2) पर होता है । 2 sec के बाद कण का विस्थापन ज्ञात कीजिये । (2) एक पिंड 20 m/s के क्षैतिज वेग से फेंका जाता है । सदिश आरेख खींचकर 5 sec पश्चात् पिंड का विस्थापन ज्ञात कीजिये । (160m) (3) एक कण x-y तल में बिंदु A(1,2) से बिंदु B तक 5 sec में गति करता है । इस अवधि के दौरान कण का विस्थापन ज्ञात कीजिये । (√10 इकाई ) (4) t=0 पर x-y तल में किसी कण का स्थिति सदिश (5) कण की स्थिति (6) किसी कण की स्थिति (7) एक समतल में गतिमान पिंड के किसी क्षण t पर निर्देशांक x=ct² तथा y=bt² है । पिंड का वेग ज्ञात कीजिये । ( (8) द्विविमीय गति में एक कण के स्थिति निर्देशांक समय के साथ निम्नानुसार परिवर्तित होते है । x=5-4t+5t², y=12-2t+3t² सभी S.I में है । ज्ञात कीजिये (a) कण की मूलबिंदु से प्रारंभिक दुरी (b) गति प्रारम्भ करने के 6 sec बाद कण की मूल बिंदु से दुरी और इसके स्थित सदिश तथा x- अक्ष के बीच बना कोण (c) गति प्रारम्भ करने के 8 sec बाद कण का वेग तथा त्वरण । ( 13 मीटर, 193.9 m , 33.8°, 88.8 m/s, 31.2° और 11.7 m/s, 31°) |
प्रक्षेप्य गति
जब किसी वस्तु को किसी प्रारंभिक वेग से ऊर्ध्वाधर के अलावा अन्य दिशा में फेंका जाता है तो वह वस्तु अचर गरुत्वीय त्वरण (g=9.8 m/s2) के अंतर्गत गति करती हुई पृथ्वी पर किसी अन्य स्थान पर गिरती है, तो वस्तु की इस गति को प्रक्षेप्य गति कहते है।
प्रक्षेप्य पथ हमेशा परवलयाकार होता है।
जैसे – तोपसे छूटा गोला , धनुष से निकला बाण , गतिमान ट्रेन की खिड़की से गिराई गयी एक वस्तु , हवाई जहाज से गिराया गया बम इत्यादि।
प्रक्षेप्य गति को सदैव दो सरल गतियों में वियोजित किया जा सकता है। क्षैतिज दिशा में गति तथा ऊर्ध्वाधर दिशा में गति , जो एक दूसरे से पूर्णतः स्वतंत्र होती है।
नोट:- क्षैतिज दिशा का गति समरूप गति होती है तथा ऊर्ध्वाधर दिशा की गति एकसमान त्वरित गति होती है।
क्षैतिज से किसी कोण पर प्रक्षेपित प्रक्षेप्य
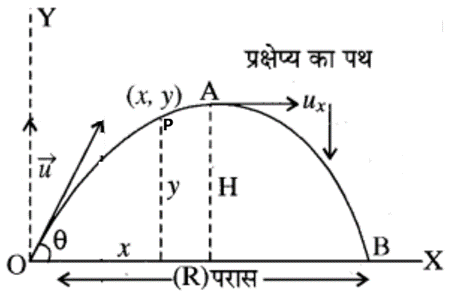
माना की एक प्रक्षेप्य t=0 समय में u वेग से क्षैतिज के साथ कोण बनाता हुआ बिंदु O से ऊपर की ओर प्रक्षेपित किया जाता है। यह उच्चतम बिंदु A से होता हुआ समान क्षैतिज तल पर बिंदु B पर गिरता है।
वस्तु पर नियत गरुत्वीय त्वरण (g) ऊर्ध्वाधर निचे की ओर लगता है।
उड्डयन काल
प्रक्षेप्य की पूरी गति में जितना समय लगता है उसे उड्डयन काल कहते है। ऐसे T द्वारा सूचित किया जाता है।
हम जानते है की
y- अक्ष की ओर (O से B तक के लिए )
क्षैतिज परास :-
प्रक्षेप्य के क्षैतिज दिशा में विस्थापन को उसका क्षैतिज परास कहते है , इसे R द्वारा सूचित किया जाता है।
हम जानते है की
x – अक्ष की ओर (O से B तक के लिए )
महत्तम ऊंचाई :-
इसे H द्वारा सूचित किया जाता है।
हम जानते है की
x- अक्ष की ओर (O से A तक के लिए )
अधिकतम क्षैतिज परास के लिए प्रक्षेपण कोण :-
हम जानते है की
R का मान महत्तम होने के लिए , का मान महत्तम होना चाहिए ।
अर्थात =1 या
अतः प्रक्षेप्य को अधिकतम दुरी तक फेंकने के लिए उसे क्षैतिज से 450 के कोण पर ऊपर की ओर प्रक्षेपित करना चाहिए।
और अधिकतम परास होगी
एक परास के लिए दो प्रक्षेपण कोण

हम जानते है की क्षैतिज से प्रक्षेपित किसी प्रक्षेप्य का परास होता है
माना की , क्षैतिज परास का मान होगा
उसी प्रकार के लिए क्षैतिज परास का मान होगा
समीकरण (1) तथा (2) के लिए
अतः यह स्पष्ट है की प्रक्षेपण कोण तथा
दोनों के लिए क्षैतिज परास का मान समान रहता है।
इन दोनों में उड्डयन काल का मान अलग अलग होगा
प्रक्षेप्य का पथ तथा समीकरण
माना, किसी क्षण t पर प्रक्षेप्य , बिंदु P(x,y) पर है।
हम जानते है की
x- अक्ष की ओर
y- अक्ष की ओर
समीकरण (1) से t का मान समीकरण (2) में रखने पर
यह समीकरण Y में एकघातीय तथा X में द्विघातीय है , जो एक परवलय को प्रदर्शित करता है। अतः स्पष्ट है की प्रक्षेप्य का पथ परवलयाकार होता है।
अब ,
किसी भी क्षण प्रक्षेप्य का वेग
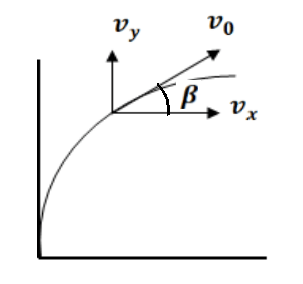
हम जानते है की
t समय के बाद प्रक्षेप्य का x- तथा y- अक्ष में वेग होगा
इसीलिए
अतः किसी भी क्षण , प्रक्षेप्य के वेग का मान होगा
इसकी दिशा हमेशा स्पर्श रेखा की दिशा की ओर होती है ।
चित्र के अनुसार
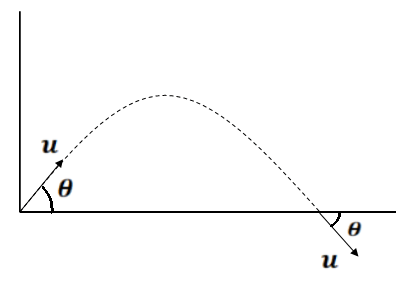
NOTE:- In projectile motion ( ground to ground) a body returns to the ground at the same angle and with the same speed at which it was projected
संख्यात्मक प्रश्न ( Numerical)(1) क्रिकेट की एक गेंद 15 m/s के वेग से क्षैतिज से 30° का कोण बनाती हुई फेंकी जाती है । यदि g=10 m/s² हो, तो ज्ञात कीजिये (a) गेंद का उड्डययन काल (b) गेंद द्वारा प्राप्त अधिकतम ऊंचाई (c) गेंद का क्षैतिज परास । ( 1.5 s , 2.81 m , 19.49 m ) (2) एक पत्थर को तल से 30° कोण पर 39.2 m/s वेग से फेंका गया तो ज्ञात कीजिये (a) उड्डययन काल (b) पत्थर का क्षैतिज परास (c) पत्थर द्वारा अधिकतम ऊंचाई ।( 4 s , 135.8 m , 19.6 m) (3) एक खिलाड़ी फुटबॉल को 20 m/s के प्रारंभिक वेग से क्षैतिज से 30° कोण पर मारता है । ज्ञात कीजिये (a) उड्डययन काल (b) अधिकतम ऊंचाई (c) पृथ्वी से टकराने पर गेंद का वेग तथा दिशा (d) क्षैतिज परास (2 sec , 5 m , 20 m/s तथा क्षैतिज से 30°, 20√3 m) (4) एक तीर हवा के छोड़ा जाता है । उसका उड्डययन काल 5 sec तथा परास 200 m है । तीर की (a) अधिकतम ऊंचाई (b) प्रक्षेपण वेग का ऊर्ध्वाधर घटक तथा क्षैतिज घटक (c) क्षैतिज से उसका कोण ज्ञात करें । ((g=9.8 m/s²) ( 30 m , 24.5 m , 40 m/s, (5) एक तोप द्वारा गोला 1000 m/s की वेग से क्षैतिज से 30° के कोण पर छोड़ा जाता है । (a) गोले को उच्चतम बिंदु तक पहुँचने पर कितना समय लगेगा (b) उसकी गति का कुल समय क्या होगा (c) गोला किस वेग से पृथ्वी पर टकराएगा ? (d) गोला कितनी ऊंचाई तक जाएगी ? (e) गोला , तोप से कितनी दूर पृथ्वी से टकराएगा ।(g=9.8 m/s²) ( 51 sec , 102 sec , 100 m/s , 12700 m , 88300 m) (6) एक प्रक्षेप्य को क्षैतिज के साथ 60° कोण बनाते हुए 30 m/s के वेग से प्रक्षेपित किया जाता है तो उच्चतम बिंदु पर उसका वेग ज्ञात कीजिये । ( 15 m/s) (7) एक तोप से 500 मीटर की क्षैतिज दुरी पर गोला फेंकना है । यदि तोप से गोला 100 m/s के वेग से फेंका जाता है , तो गोले का प्रक्षेपण कोण कितना होना चाहिए ? ((g=10 m/s² ) ( 15° या 75°) (8) एक तोप 15 m/s के वेग से गोला फेंक सकती है । इससे 11.25 m की दुरी पर गोला फेंकना हो , तो गोले का प्रक्षेपण कोण ज्ञात कीजिये । (15° या 75°) (9) 100 m ऊँचे टावर के पैंदे से 200 m की दुरी से गोली इस प्रकार चलाई जाती है की वह उस टावर को पार कर जाये । गोली के वेग का परिमाण तथा दिशा ज्ञात करें । (62.6 m/s , 45° क्षैतिज से ) (10) एक प्रक्षेप्य जिसका द्रव्यमान 50 ग्राम है, को क्षैतिज से 30° कोण पर 10 m/s के वेग से फेंका जाता है तो उच्चतम बिंदु पर ज्ञात कीजिये । (a) रेखीय संवेग तथा (b) गतिज ऊर्जा । (0.43 kgm/s, 1.875 जूल ) (11) क्रिकेट का एक खिलाडी अधिकतम 100 मीटर की क्षैतिज दुरी तक गेंद फेंक सकता है । वही खिलाड़ी अधिकतम किस ऊंचाई तक गेंद फेंक सकेगा ? (50 m) (12) एक पिंड को 40 m/s के वेग से प्रक्षेपित किया जाता है वह 2 s पश्चात् एक 20.4 m लम्बे खम्बे को पार कर जाता है तो प्रक्षेपण कोण तथा क्षैतिज परास ज्ञात करे । (30°, 141.4 m) (13) एक गेंद ऊर्ध्वाधर से 45° के कोण पर प्रक्षेपित की जाती है और वह प्रक्षेपण बिंदु से 2 मीटर पर स्थित एक दीवार को ठीक पर करती है । यदि गेंद दीवार के दूसरी ओर दीवार से 4 मीटर की दुरी पर जमीन पर गिरे , तो दीवार की ऊंचाई ज्ञात कीजिये । (4/3 m) (14) एक हाल की ऊंचाई 25 m है । 40 m/s के वेग से हाल में प्रक्षेपित एक बाल बिना छत से टकराये अधिकतम कितनी क्षैतिज दुरी तक जा सकती है । (g=9.8 m/s² (15) एक प्रक्षेप्य को क्षैतिज से 60° कोण पर 20 m/s वेग से दागा जाता है । एक बस 5 m/s की चाल से क्षैतिज सड़क पर चल रही है । जब प्रक्षेप्य को दागा जाता है तो बस 50 m आगे होती है । बस के पिछले हिस्से से टकराने के लिए प्रक्षेप्य द्वारा लिया गया समय ज्ञात कीजिये (10 s) |
क्षैतिज दिशा में प्रक्षेपित प्रक्षेप्य :-
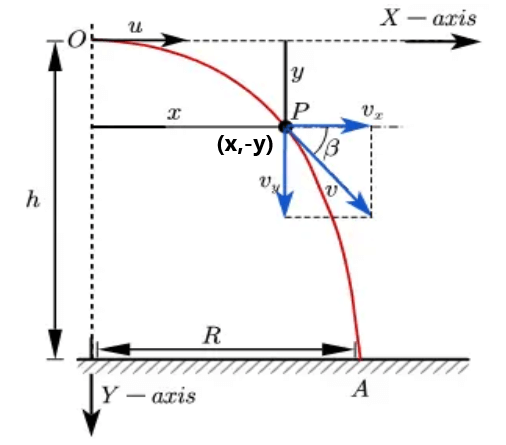
माना एक प्रक्षेप्य को पृथ्वी तल से h ऊंचाई पर स्थित एक बिंदु O से क्षैतिज दिशा में u वेग से प्रक्षेपित किया जाता है। यह अचर गुरुत्वीय त्वरण ‘g’ के अंतर्गत गति करता हुआ t समय में पृथ्वी तल पर बिंदु A पर गिरता है।
उड्डययन काल
हम जानते है की
y-aksh की ओर
क्षैतिज परास
हम जानते है की
x- अक्ष की ओर
प्रक्षेप्य का पथ तथा समीकरण
माना की t समय में प्रक्षेप्य p बिंदु पर है। इस समय में कण का X- अक्ष तथा Y- अक्ष में विस्थापन क्रमशः x और y है।
x- अक्ष की ओर
उसी प्रकार y- अक्ष की ओर
यह एक परवलय का समीकरण है अतः क्षैतिज दिशा में प्रक्षेपित प्रक्षेप्य का पथ परवलयाकार होता है।
किसी भी क्षण प्रक्षेप्य का वेग
हम जानते है की
t समय के बाद प्रक्षेप्य का x- तथा y- अक्ष में वेग होगा
तथा
∴ t समय बाद प्रक्षेप्य का वेग होगा
चित्र के अनुसार
संख्यात्मक प्रश्न ( Numerical)(1) एक गेंद को क्षैतिज दिशा में 15 m/s वेग से फेंका जाता है । 0.3 sec में उसके वेग के क्षैतिज तथा ऊर्ध्व घटक क्या होंगे ? वह क्षैतिज से 45° कोण बनाने के लिए कितना समय लेगा ? (15 m/s, 2.94 m/s , 1.53 s) (2) एक पत्थर को किसी टावर से 25 m की ऊंचाई से क्षैतिज दिशा में 15 m/s के वेग से फेंका गया है । ज्ञात कीजिये (a) समय जिसमे पत्थर गतिशील रहेगा (b) टावर के पैंदे से वह दुरी जहाँ पर पत्थर गिरता है (c) वह वेग जिससे वह तल को छूता है (d) पत्थर के पथ द्वारा क्षैतिज से बनाया गया कोण जब वह तल पर पहुंचता है । (2.26 m , 33.9 m , 26.75 m/s, 55°54′) (3) एक लड़ाकू विमान 150 m/s के वेग से 500 m ऊंचाई पर क्षैतिज उड़ रहा है । इससे एक बम लक्ष्य की ओर छोड़ा जाता है । ज्ञात कीजिये (a) लक्ष्य तक पहुँचने में गेंद द्वारा लिया गया समय (b) वह वेग जिससे बम लक्ष्य से टकराता है (c) लक्ष्य की दुरी (g=10 m/s²) ( 10 sec , 180 m/s, 1500 m) (4) किसी टावर से एक पत्थर को 15 m/s के क्षैतिज वेग से फेंका जाता है । यदि पत्थर टॉवर के पैंदे से 100 मीटर दुरी पर जा कर गिरता है तो टॉवर की ऊंचाई ज्ञात कीजिये । (217.99 m) (5) एक टॉवर जो की 100 m ऊँचा है , से एक गेंद को 10 m/s के क्षैतिज वेग से फेंका जाता है । तो ज्ञात कीजिये (a) जमीन तक पहुँचने में गेंद द्वारा लिया गया समय (b) वेग जिससे वह सतह पर टकराती है । (4.5 s , 45.22 m/s) (6) एक पिंड को टॉवर से क्षैतिज दिशा में फेंका जाता है तथा क्षैतिज से 45° का कोण बनाते हुए 3 sec बाद जमीन पर गिरती है । टॉवर की ऊंचाई तथा वह चाल ज्ञात कीजिये जिससे पिंड को प्रक्षेप्य किया गया है । (g=9.8 m/s²) ( 44.1 m , 29.4 m/s) (7) एक 50 m ऊँचे टॉवर से एक पत्थर के क्षैतिज दिशा में फेंका जाता है । यदि पत्थर के पैंदे से 20 m दुरी पर पत्थर जाकर गिरता है तो वह वेग ज्ञात कीजिये जिससे पत्थर को फेंका गया था । (6.26 m/s) (8) एक लड़ाकू वायुयान 2000 मीटर की ऊंचाई पर 540 km/h वेग से क्षैतिज उड़ रहा है । इसे शत्रु के कैंप से बम कितनी दूर गिराना चाहिए ताकि यह कैंप से टकरा जाये ? (g=10 m/s²) (3km) (9) एक लड़का गेंद को जमीन से 500 m ऊंचाई वाली ईमारत की खिड़की से क्षैतिज दिशा में फेंकता है जिससे यह दूसरी इमारत में जमीन से 10 m ऊपर स्थित खिड़की में प्रवेश कर जाती है । यदि दोनों इमारत 100 मीटर दुरी पर हो तो गेंद क्षैतिज वेग ज्ञात कीजिये । (10 m/s) (10) एक गेंद को h ऊंचाई से क्षैतिज दिशा में (11) एक वायुयान क्षैतिज तल से 600 km/h के वेग से 1960 मीटर की ऊंचाई पर उड़ रहा है । जब यह पृथ्वी के बिंदु A के ठीक ऊपर होता है , इससे एक वस्तु गिराई जाती है जो पृथ्वी पर बिंदु B पर गिरती है । A से B तक की दुरी की गणना कीजिये । (3.33 km ) (12) एक खिलाड़ी क्षैतिज से 30° के कोण पर ऊपर की ओर 14 m/s के वेग से गोला फेंकता है । यदि प्रक्षेपण बिंदु पृथ्वी से 12 मीटर की ऊंचाई पर हो तो खिलाड़ी के गोला फेंकने की क्षैतिज दुरी बताइये । (29.1 मीटर ) (13) एक पुल से एक पत्थर क्षैतिज से निचे की ओर 30° के कोण पर 25 m/s के वेग से फेंका जाता है । यदि पत्थर 2.5 sec में जल से टकराता है तो जल के पृष्ठ से पुल की ऊंचाई कितनी है । (g=9.8 m/s²) ( 61.9 m) (14) एक इमारत के शिखर से ऊपर की ओर एक गेंद को क्षैतिज से 30° कोण पर 30 m/s के वेग से प्रक्षेपित किया जाता है । यदि इमारत 100 मीटर ऊँची हो तो गेंद को जमीन तक पहुँचने में कितना समय लगेगा ? (6.3 sec) |
प्रश्न(1) एक पत्थर को अधिकतम क्षैतिज परास से फेंकने पर वह कितना कोण बनाएगा ? |
रिक्त स्थानों की पूर्ति करो(1) वृत्ताकार गति तथा प्रक्षेप्य गति दोनों ही __________ गति के उदाहरण है । |
